ARITMÉTICA MERCANTIL (FORMULARIOS)

Aritmética Mercantil

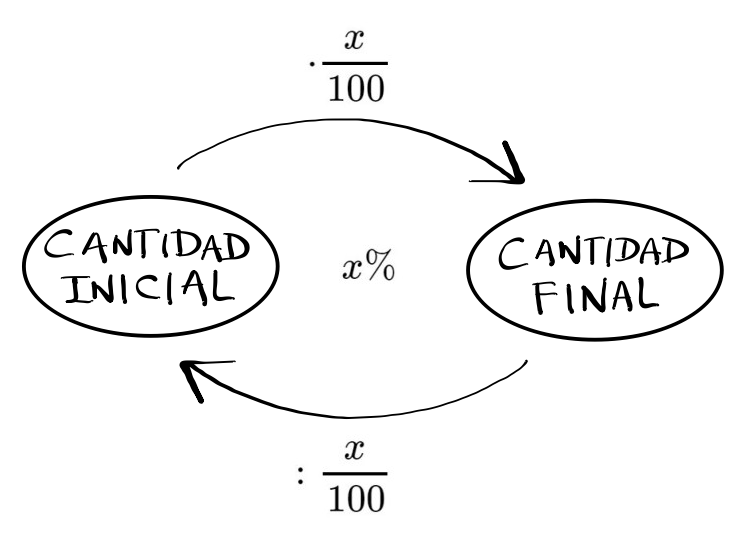
• Porcentajes

$$ x \% \hbox{ de C } = \frac{x}{100} \cdot C \Rightarrow \left\{\begin{array}{l} CF=CI \cdot \displaystyle{\left( \frac{x}{100} \right)}\\ CI= \displaystyle{\frac{CF}{\displaystyle{\left( \frac{x}{100} \right)}}}\\ \displaystyle{\left( \frac{x}{100} \right)}=\frac{CF}{CI}\\ \end{array}\right. $$


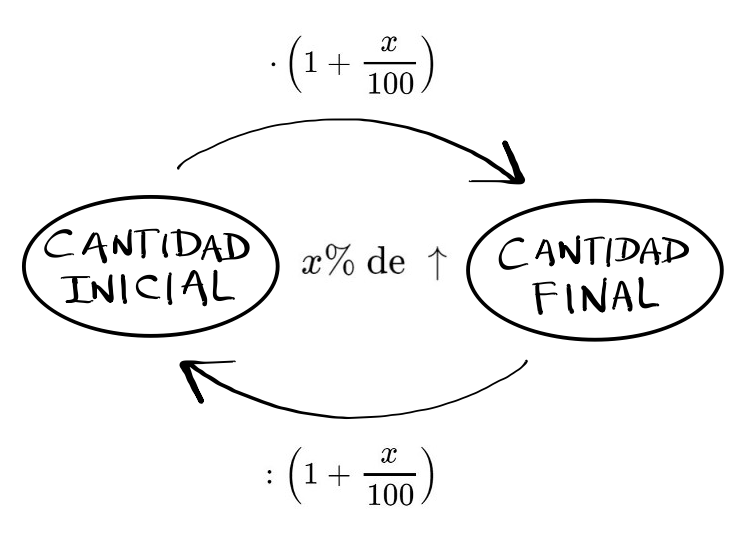
• Aumentos porcentuales

$$ \hbox{ Un aumento porcentual del } x \% \hbox{ de C } =\left(1+\frac{x}{100}\right) \cdot C \Rightarrow \left\{\begin{array}{l} CF=CI \cdot \displaystyle{\left( 1+\frac{x}{100} \right)}\\ CI= \displaystyle{\frac{CF}{\displaystyle{\left( 1+\frac{x}{100} \right)}}}\\ \displaystyle{\left( 1+\frac{x}{100} \right)}=\frac{CF}{CI}\\ \end{array}\right. $$ $$ \hbox{ El índice de variación es } \left(1+\frac{x}{100}\right)$$


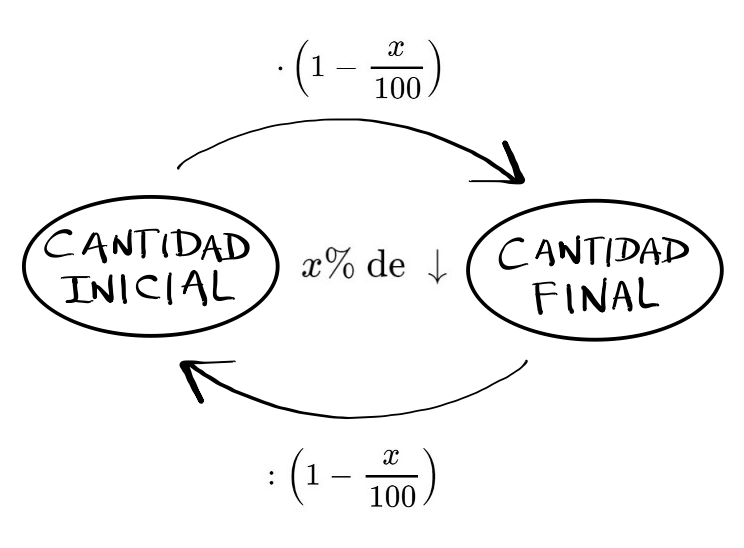
• Descuentos porcentuales

$$ \hbox{ Un descuento porcentual del } x \% \hbox{ de C } =\left(1-\frac{x}{100}\right) \cdot C \Rightarrow \left\{\begin{array}{l} CF=CI \cdot \displaystyle{\left( 1-\frac{x}{100} \right)}\\ CI= \displaystyle{\frac{CF}{\displaystyle{\left( 1-\frac{x}{100} \right)}}}\\ \displaystyle{\left( 1-\frac{x}{100} \right)}=\frac{CF}{CI}\\ \end{array}\right. $$ $$ \hbox{ El índice de variación es } \left(1-\frac{x}{100}\right)$$


• Porcentajes encadenados

Para calcular aumentos y descuentos porcentuales encadenados, multiplicamos los sucesivos índices de variación correspondientes a cada uno de los aumentos o descuentos porcentuales, obteniendo el índice de variación del porcentaje total equivalente a la realización de cada uno de dichos porcentajes encadenados por separado.

$$ \hbox{ El índice de variación total es } \left(1 \pm \frac{x_{1}}{100}\right) \cdot \left(1 \pm \frac{x_{2}}{100}\right) \cdots \left(1 \pm \frac{x_{k}}{100}\right)$$

• Definiciones

Año comercial: 12 meses de 30 días (360 días en total)

Capital inicial: Cantidad de dinero prestada o depositada \( \hbox{} (c=c_{i}) \)

Capital final: Cantidad de dinero inicial prestada o depositada más los intereses obtenidos \( \hbox{} (C=c_{f}) \)

Tiempo: Duración del préstamo solicitado o depósito, expresado en años \( \hbox{} (t) \)

Rédito: Tanto por ciento o tipo de interés anual (beneficio que producirían 100 € en un año) \( \hbox{} (r\%) \)

Tanto por uno (beneficio que producirían 1 € en un año) \( \hbox{} (i=\frac{r}{100}) \)

Interés: Beneficio que produce el capital prestado o depositado \( \hbox{} (I) \)

• Tipos de Interés

Interés simple: Es aquel que no se acumula al capital para generar más intereses. El capital inicial, por tanto, permanece invariable y el beneficio que se obtiene se debe únicamente al capital inicial.

$$\left.\begin{array}{cccc} \displaystyle{I=c \cdot i \cdot t} & donde & i=\frac{r}{100}, & \hbox{ (t en años) }\\ \end{array}\right.$$ $$\left.\begin{array}{c} \displaystyle{C=c + I}\\ \end{array}\right.$$


Interés compuesto: Es aquel que se acumula al capital para ir generando nuevos intereses. Al capital inicial se le van sumando los intereses de cada periodo (por lo que va aumentando, en lugar de permanecer fijo como en el interés simple).

$$\left.\begin{array}{cccc} \displaystyle{C=c \left( 1+i \right)^t}, & donde & i=\frac{r}{100}, & \hbox{ (t en años) }\\ \end{array}\right.$$ $$\left.\begin{array}{c} \displaystyle{I=C - c}\\ \end{array}\right.$$

Periodos de capitalización: Un periodo de capitalización es el intervalo de tiempo al final del cual se cobran los intereses. Puede ser anual, semestral, trimestral, mensual o diario. Si el tiempo que se deposita el dinero no es un año, se cobra la parte proporcional del interés anual.

Si depositando un capital c, los intereses se abonan n veces al año con un rédito r% anual durante t años a interés compuesto, el capital final C será:

$$\left.\begin{array}{cccc} \displaystyle{C=c\left( 1+\frac{i}{n} \right)^{n \cdot t}}, & donde & i=\frac{r}{100}, & n=\left\{\begin{array}{lll} 1 & \hbox{ (año) }\\ 2 & \hbox{ (semestres) }\\ 4 & \hbox{ (trimestres) }\\ 12 & \hbox{ (meses) }\\ 360 & \hbox{ (días) }\\ \end{array}\right. \\ \end{array}\right. $$ $$\left.\begin{array}{c} \displaystyle{I=C - c}\\ \end{array}\right.$$


• T.A.E. (Tasa Anual Equivalente)

Es el tanto por ciento de aumento total del capital en un año. Es simplemente el cálculo del tipo de interés anual, según las fórmulas del interés compuesto (No tiene por qué ser igual al rédito pues depende del número de capitalizaciones al año)

$$\hbox{ T.A.E. } =\left.\begin{array}{cccc} \displaystyle{\left( 1+\frac{i}{n} \right)^n -1}, & donde & i=\frac{r}{100}, & n=\left\{\begin{array}{lll} 1 & \hbox{ (año) }\\ 2 & \hbox{ (semestres) }\\ 4 & \hbox{ (trimestres) }\\ 12 & \hbox{ (meses) }\\ 360 & \hbox{ (días) }\\ \end{array}\right. \\ \end{array}\right. $$

En las cuentas de ahorro, cuando los periodos de capitalización son inferiores a un año, los intereses anuales producidos por un cierto capital son superiores al rédito que declara el banco. Se llama Tasa Anual Equivalente (T.A.E.) al % de crecimiento total del capital durante un año. 


En los préstamos bancarios, la T.A.E. es, también, superior al rédito declarado. Al calcularla se incluyen los pagos fijos (comisiones y gastos) que cobra el banco por conceder el préstamo. 




• Financiación (Amortización de préstamos)

La financiación o amortización de un préstamo consiste en devolver el dinero prestado y los intereses que ese dinero prestado genera en varios plazos aplazados.

• Cada pago salda los intereses que produce la deuda pendiente desde el pago anterior y, el resto, amortiza parte de esa deuda.
• El último pago salda los intereses pendientes desde el pago anterior y amortiza la totalidad de la deuda pendiente.
• Lo habitual es que todos los pagos sean idénticos. Ahora veremos cómo calcular esa cantidad fija (cuota, mensualidad o anualidad) que permite amortizar el total de la deuda en un número prefijado de plazos.

Si se ha de amortizar un préstamo C, a un interés del r% anual, mediante n pagos al año (anualidades, mensualidades,...) durante t años, la cuota periódica c se calcula mediante:

$$\left.\begin{array}{c} \displaystyle{c=C\frac{\left(1+\frac{i}{n}\right)^{n \cdot t} \cdot \frac{i}{n}}{\left( 1+\frac{i}{n} \right)^{n \cdot t} -1}} \end{array}\right. $$ $$\left.\begin{array}{ccc} donde & i=\frac{r}{100}, & n=\left\{\begin{array}{lll} 1 & \hbox{ (año) }\\ 2 & \hbox{ (semestres) }\\ 4 & \hbox{ (trimestres) }\\ 12 & \hbox{ (meses) }\\ 360 & \hbox{ (días) }\\ \end{array}\right. \\ \end{array}\right. $$

En el caso particular de un pago al año, se denomina anualidad y se calcula mediante:

$$\left.\begin{array}{ccc} \displaystyle{c=C\frac{\left( 1+i \right)^t \cdot i}{\left( 1+i \right)^t -1}}, & donde & i=\frac{r}{100}\\ \end{array}\right. $$

En el caso particular de pagos mensuales, se denomina mensualidad y se calcula mediante:

$$\left.\begin{array}{ccc} \displaystyle{c=C\frac{\left( 1+\frac{i}{12} \right)^{12t} \cdot \frac{i}{12}}{\left( 1+\frac{i}{12} \right)^{12t} -1}}, & donde & i=\frac{r}{100}\\ \end{array}\right. $$


• Capitalización

La capitalización consiste en entregar al banco determinadas cantidades de dinero en periodos regulares, con objeto de tener al final un capital formado por las aportaciones periódicas más los intereses generados.

El capital final C obtenido al aportar una cuota periódica c, a un interés del r% anual, mediante n pagos al año (anualidades, mensualidades,...) durante t años es:

$$\left.\begin{array}{c} \displaystyle{C=\frac{c \cdot \left[ \left( 1+\frac{i}{n} \right)^{n \cdot t+1}-(1+\frac{i}{n}) \right]}{\frac{i}{n}}} \\ \end{array}\right.$$ $$\left.\begin{array}{cccc} donde & c=\hbox{cuota}, & i=\frac{r}{100}, & n=\left\{\begin{array}{lll} 1 & \hbox{ (año) }\\ 2 & \hbox{ (semestres) }\\ 4 & \hbox{ (trimestres) }\\ 12 & \hbox{ (meses) }\\ 360 & \hbox{ (días) }\\ \end{array}\right. \\ \end{array}\right. $$

En el caso particular de un pago al año, se denomina anualidad y se calcula mediante:

$$ \left.\begin{array}{ccccc} \displaystyle{C=\frac{a \cdot \left[ \left( 1+i \right)^{t+1}-(1+i) \right]}{i}}, & donde & a=\hbox{anualidad}, & i=\frac{r}{100}\\ \end{array}\right. $$

Otros resultados teóricos importantes

Progresiones geométricas

Una progresión geométrica es una sucesión en la que cada término se obtiene del anterior multiplicando por una cantidad constante \( r \) llamada razón.

$$ \left\{\begin{array}{ll} r=\displaystyle{\frac{a_{k+1}}{a_k}}, \forall k \in \mathbb{N} & \mathbf{\hbox{ (Razón) }}\\ a_n=\displaystyle{a_1 \cdot r^{n-1}} & \mathbf{\hbox{ (Término general) }}\\ a_n=\displaystyle{a_k \cdot r^{n-k}} & \mathbf{\hbox{ (Interpolación de términos) }}\\ S_n=\displaystyle{\frac{a_n \cdot r - a_1}{r-1}}=\displaystyle{\frac{a_{1} \cdot (r^{n} - 1)}{r-1}}, r \neq 1 & \mathbf{\hbox{ (Suma de los n primeros términos) }}\\ S=\displaystyle{\frac{a_1}{1-r}}, |r| \lt 1 & \mathbf{\hbox{ (Suma de los infinitos términos) }}\\ \end{array}\right. $$

• La suma de los n primeros términos de una progresión geométrica es

  $$S_{n}=\frac{a_{1} \cdot (r^{n} - 1)}{r-1}$$

  Demostración:

  Teniendo en cuenta que: $$S_n = a_1 + a_2 + \cdots + a_n$$ $$r=\displaystyle{\frac{a_{n+1}}{a_n}} \Rightarrow a_{n+1}=r \cdot a_{n}$$
  Multiplicando por la razón y restando ambas igualdades: $$r \cdot S_{n}=r \cdot (a_{1}+a_{2}+ \cdots + a_{n-1}+a_{n}) = $$ $$ = r \cdot a_{1}+r \cdot a_{2}+ \cdots + r \cdot a_{n-1}+r \cdot a_{n}) = $$ $$ = a_{2}+a_{3}+ \cdots + a_{n}+a_{n+1}$$ $$ \left\{\begin{array}{l} r \cdot S_n = a_{2}+a_{3}+ \cdots + a_{n}+a_{n+1}\\ -S_n = - (a_{1}+a_{2}+ \cdots + a_{n-1}+a_{n})\\ \end{array}\right. \Rightarrow $$
  $$ \Rightarrow \left\{\begin{array}{l} r \cdot S_n = a_{2}+a_{3}+ \cdots + a_{n}+a_{n+1}\\ -S_n = -a_{1}-a_{2}- \cdots - a_{n-1}-a_{n}\\ \end{array}\right.$$
  Sumando ambas expresiones: $$(r-1) \cdot S_n = a_{2}+a_{3}+ \cdots + a_{n}+a_{n+1} - a_{1} - a_{2} - \cdots - a_{n-1} - a_{n} \Rightarrow $$ $$\Rightarrow (r-1) \cdot S_n = a_{n+1} - a_{1} \Rightarrow $$ $$S_n = \frac{a_{n+1} - a_{1}}{r-1} = \frac{a_{1} \cdot r^{n} - a_{1}}{r-1} = \frac{a_{1} \cdot (r^{n} - 1)}{r-1}$$

• La suma de los infinitos términos de una progresión geométrica es

  $$S_{\infty}= \displaystyle{\frac{a_{1}}{1-r}}$$

  Demostración:

  $$S_{\infty}=\displaystyle{\lim_{n \rightarrow \infty} S_{n}} =\displaystyle{\lim_{n \rightarrow \infty} \frac{a_{1} \cdot (r^{n} - 1)}{r-1}} = \frac{-a_{1}}{r-1} = \displaystyle{\frac{a_{1}}{1-r}} $$