2ºBACH CCSS INTEGRALES (CUESTIONES)
Integral indefinida. Integral definida. Aplicaciones de la integral
Cuestión (#1)
Prueba que si \(F: \mathbb{D} \rightarrow \mathbb{R}\) es una primitiva de la función \(f\), entonces lo es también la función \(x \in \mathbb{D} \rightarrow F(x)+C\), donde \(C\) es una constante cualquiera.
Solución:
Si \(F(x)\) es una primitiva de \(f(x) \Rightarrow F'(x)=f(x)\)
Aplicando la linealidad de la derivada:
\(\left(F(x)+C\right)'=F'(x)+C'=f(x)+0=f(x) \Rightarrow F(x)+C\) es también una primitiva de \(f(x)\)
Cuestión (#2)
Consideremos la función \(f\) definida por \(f(x)=\displaystyle{\frac{1}{x}}, x \neq 0\). ¿Es una primitiva de \(f\) la función \(F\) definida por \(F(x)=Ln(x), x >0\)?
Solución:
No, ya que \(F'(x)=\left(Ln(x)\right)'=\displaystyle{\frac{1}{x}}, x >0\) es la rama derecha de la hipérbola \(y=\displaystyle{\frac{1}{x}}\), y sin embargo, la función dada \(y=\displaystyle{\frac{1}{x}}, x \neq 0\), es la hipérbola completa.
Cuestión (#3)
Dos funciones \(f\) y \(g\) tienen la misma función derivada.
¿Es entonces \(f-g\) una función constante?
-
¿Es \(f-g\) constante en cada intervalo del dominio de derivabilidad?
Solución:
Si dos funciones \(f\) y \(g\) tienen la misma función derivada, entonces se diferencian en una constante:
\(f'(x)=g'(x) \Rightarrow \displaystyle{\int{f'(x)dx}}=\displaystyle{\int{g'(x)dx}} \Rightarrow f(x)+C_1=g(x)+C_2 \Rightarrow f(x)-g(x)=C_2-C_1 \Rightarrow f(x)-g(x)=C\)
-
No, ya que puede ser una función a trozos y ambas funciones se diferenciarían en una constante en cada trozo, por lo que en cada trozo sería constante, pero ambas constantes puden ser distintas.
-
Sí, en cada intervalo del dominio de derivabilidad sería constante.
Cuestión (#4)
Una función coincide en todo punto con su derivada. ¿De qué función puede tratarse?
Solución:
Caso 1: \(f(x)=0 \Rightarrow f'(x)=0\)
Caso 2: \(f(x)=e^{x} \Rightarrow f'(x)=e^{x}\)
Cuestión (#5)
Comprueba que si \(n \neq 1\), \(\displaystyle{\int{\frac{1}{x^n}dx}}=\displaystyle{\frac{-1}{(n-1)x^{n-1}}}+C\)
Solución:
Sea \(F(x)=\displaystyle{\frac{-1}{(n-1)x^{n-1}}}+C, n \neq 1\).
Sea \(F'(x)=\left(\displaystyle{\frac{-1}{(n-1)x^{n-1}}}+C\right)'=\left(\displaystyle{\frac{-1}{(n-1)}} \cdot \displaystyle{\frac{1}{x^{n-1}}}\right)'+C'=\displaystyle{\frac{-1}{(n-1)}} \cdot \left(\displaystyle{\frac{1}{x^{n-1}}}\right)'+0=\).
\(=\displaystyle{\frac{-1}{(n-1)}} \cdot \displaystyle{\frac{1' \cdot x^{n-1} - 1 \cdot (n-1)x^{n-1-1}}{\left(x^{n-1}\right)^2}}=\displaystyle{\frac{-1}{(n-1)}} \cdot \displaystyle{\frac{0 \cdot x^{n-1} - 1 \cdot (n-1)x^{n-2}}{x^{2(n-1)}}}=\).
\(=\displaystyle{\frac{-1}{(n-1)}} \cdot \displaystyle{\frac{-(n-1)x^{n-2}}{x^{2n-2}}}=\displaystyle{\frac{(n-1)x^{n-2}}{(n-1)x^{2n-2}}}=\displaystyle{\frac{1}{x^{(2n-2)-(n-2)}}}=\displaystyle{\frac{1}{x^{2n-2-n+2}}}=\displaystyle{\frac{1}{x^{n}}}, n \neq 1\).
Cuestión (#6)
Una primitiva de la función continua \(f(x)\) es la función \(F(x)\). Obtén una primitiva de \(f\) que pase por el origen de coordenadas.
Solución:
Si una primitiva de la función continua \(f(x)\) es la función \(F(x) \Rightarrow\) La función \(y=F(x)+C\), \(C\) constante, también es una primitiva de \(f(x)\).
Si pasa por el punto \((0,0)\), sustituyendo en \(y=F(x)+C\) se obtiene que: \(F(0)+C=0 \Rightarrow C=-F(0)\)
Por tanto, la primitiva buscada es \(y=F(x)-F(0)\).
Cuestión (#7)
Si la gráfica de una función \(y=f(x)\) es una línea recta. ¿Cómo es la gráfica de una primitiva de ella?
Solución:
La ecuación de una recta es \(f(x)=ax+b, a \neq 0\).
Una primitiva suya es de la forma \(F(x)=\displaystyle{\int{\left(ax+b\right)dx}}, a \neq 0\).
\(F(x)=\displaystyle{\int{\left(ax+b\right)dx}}=\displaystyle{a\int{xdx}}+\displaystyle{b\int{1dx}}=\displaystyle{a\left(\frac{x^2}{2}\right)}+bx+C=\displaystyle{\frac{ax^2}{2}}+bx+C, a \neq 0\)
Por tanto, la gráfica de una primitiva suya es una parábola.
Cuestión (#8)
Obtén una primitiva de la función representada a continuación:
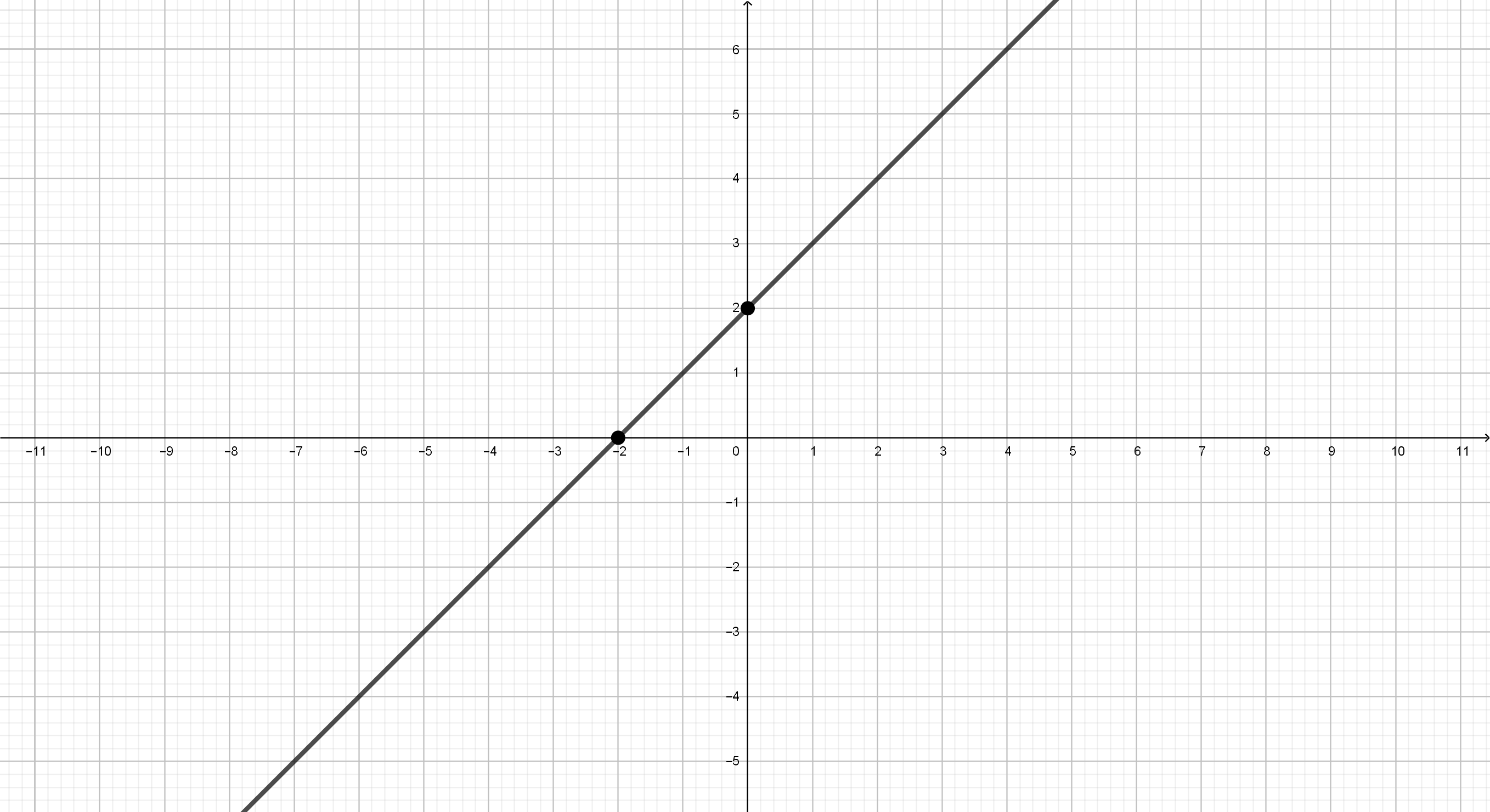
Solución:
La ecuación de la recta que pasa por los puntos \(A(-2,0)\) y \(B(0,2)\) es \(y=x+2\).
\(\overrightarrow{AB}=B-A=(0,2)-(-2,0)=(2,2) \Rightarrow \left\{\begin{array}{l} m=\displaystyle{\frac{2}{2}}=1\\ n=2\\ \end{array}\right.\)
Una primitiva suya es de la forma \(F(x)=\displaystyle{\int{\left(x+2\right)dx}}\).
\(F(x)=\displaystyle{\int{\left(x+2\right)dx}}=\displaystyle{\int{xdx}}+\displaystyle{2\int{1dx}}=\displaystyle{\frac{x^2}{2}}+2x+C\)
Por tanto, la gráfica de una primitiva suya es una parábola \(y=\displaystyle{\frac{x^2}{2}}+2x\) y las traslaciones verticales de \(C\) unidades de la misma.
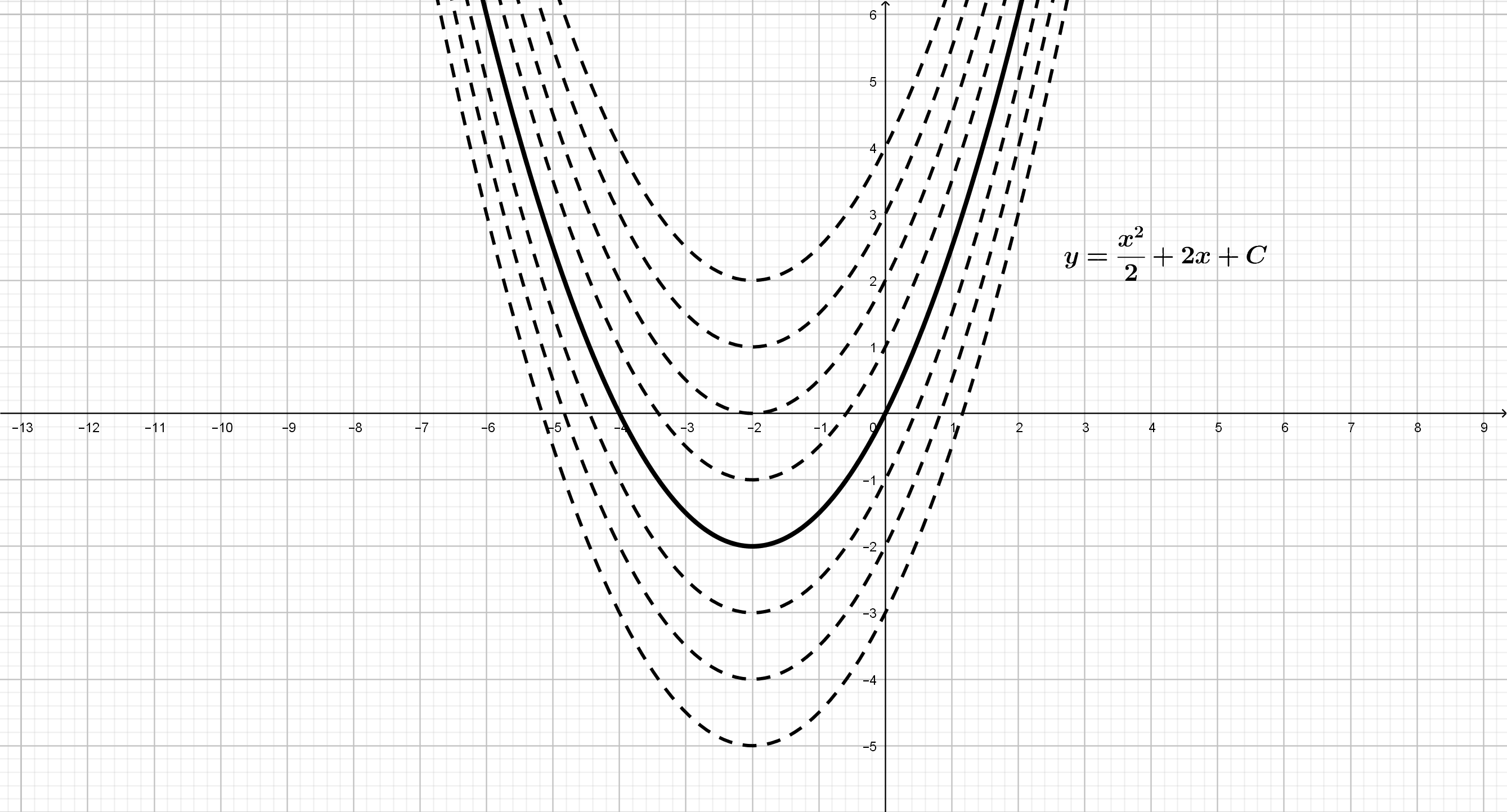
Cuestión (#9)
Comprueba que \(\displaystyle{\int{2x cos(x)dx}} \neq x^2sen(x)+C\)
Solución:
Sea \(F(x)=x^2sen(x)+C\) y \(f(x)=2x cos(x)\)
Queremos comprobar que \(F(x) \neq \displaystyle{\int{f(x)dx}} \Rightarrow F'(x) \neq f(x)\)
Aplicando la regla de la cadena:
\(F'(x)=\left(x^2sen(x)+C\right)'= \left(x^2sen(x)\right)'+C'= 2x sen(x)+x^2 (-cos(x))+0=\)
\(= 2x sen(x)-x^2 cos(x) \neq 2x cos(x) = f(x)\)
Cuestión (#10)
Tras analizar la cuestión anterior, ¿Es la integral indefinida de un producto el producto de las integrales indefinidas de los factores?
Solución:
No, ya que la Cuestión (#9) es un ejemplo donde no se cumple. De ser cierto, debería cumplirse siempre.
Cuestión (#11)
Halla \(f(x)\) sabiendo que:
- \(\displaystyle{\int{f(x)dx}}=x^3-x+C\)
- \(\displaystyle{\int{f(x)dx}}=Ln(3x+1)+C\)
- \(\displaystyle{\int{f(x)dx}}=sen(2x+1)+C\)
Solución:
- \(F(x)=x^3-x+C \Rightarrow f(x)=F'(x)=\left(x^3-x+C\right)'=3x^2-1+0=3x^2-1\)
- \(F(x)=Ln(3x+1)+C \Rightarrow f(x)=F'(x)=\left(Ln(3x+1)+C\right)'=\displaystyle{\frac{3}{3x+1}}+0=\displaystyle{\frac{3}{3x+1}}\)
- \(F(x)=sen(2x+1)+C \Rightarrow f(x)=F'(x)=\left(sen(2x+1)+C\right)'=2cos(2x+1)+0=2cos(2x+1)\)
Cuestión (#12)
Obtén la función \(u\) sabiendo que \(\displaystyle{\int{2xcos(x^2)dx}}=u(x^2)+C\)
Solución:
\(u(x)=sen(x)\)
Aplicando la regla de la cadena: \(\left(sen(x^2)+C\right)'=2xcos(x^2)\).
Cuestión (#13)
Dada la función \(f: \mathbb{R}-\{0\} \rightarrow \mathbb{R}\) definida por \(f(x)= \left\{\begin{array}{lcc} 1 & si & x < 0\\ 2x & si & x > 0\\ \end{array}\right.\), encuentra una función continua \(F: \mathbb{R} \rightarrow \mathbb{R}\) tal que
- \(F'(x)=f(x),x \neq 0\)
- \(F(0)=5\)
¿Es \(F\) derivable para \(x=0\)?
Solución:
\(F(x)\) se obtiene integrando cada uno de los trozos de la función \(f(x)\):
\(F(x)=\left\{\begin{array}{lcc} x+C_1 & si & x < 0\\ x^2+C_2 & si & x > 0\\ \end{array}\right.\)
Como \(F(x)\) es continua en \(x=0\):
- \(F(0)=5\)
- \(\left\{\begin{array}{l} F(0^{-}=\displaystyle{\lim_{x \rightarrow 0^{-}} (x+C_1)}=0+C_1=C_1\\ F(0^{+}=\displaystyle{\lim_{x \rightarrow 0^{+}} (x^2+C_2)}=0^2+C_2=C_2\\ \end{array}\right.\Rightarrow C_1=C_2=5\)
\(F(x)=\left\{\begin{array}{lcc} x+5 & si & x \leq 0\\ x^2+5 & si & x > 0\\ \end{array}\right.\)
Pero \(F(x)\) no es derivable para \(x=0\), ya que su derivada es \(f(x)\) y no es continua para \(x=0\) al no estar definida para ese valor.
Cuestión (#14)
Demuestra que \(f: \mathbb{R} \rightarrow \mathbb{R}\) definida por \(f(x)= \left\{\begin{array}{lcc} 1 & si & x \leq 0\\ 2x & si & x > 0\\ \end{array}\right.\), no es la función derivada de ninguna \(F: \mathbb{R} \rightarrow \mathbb{R}\).
Solución:
Si cierta función \(F(x)\) fuera una primitiva de \(f(x)\), entonces \(F(x)\) sería derivable y \(F'(x)=f(x)\).
Como ser derivable implica ser continua, entonces \(f(x)\) sería continua en \(\mathbb{R}\), pero \(f(x)\) no es continua en \(x=0\) porque no coinciden los límites laterales cuando \(x \rightarrow 0\).
Continuidad en \(x=0\)
\(\left. \begin{array}{l} 1) f(0)=1\\ 2) \displaystyle\lim_{x \rightarrow 0} f(x)= \left \{ \begin{array}{l} \displaystyle\lim_{x \rightarrow 0^{-}} 1=1\\ \displaystyle\lim_{x \rightarrow 0^{+}} 2x=2 \cdot 0=0\\ \end{array} \right.\\ \end{array} \right\} \Rightarrow f(x)\) no es continua en \(x=0\)

