ESTADÍSTICA UNIDIMENSIONAL (FORMULARIOS)

Estadística Unidimensional

$$\left.\begin{array}{l} X= \hbox{ Variable estadística },\hbox{ } n=\hbox{ Tamaño muestral} \\ x_1, x_2, \cdots, x_k, \hbox{ los distintos valores que toma la variable en dicha muestra, donde } x_1 < x_2 < \cdots < x_k \end{array}\right.$$

Frecuencias

$$\left\{\begin{array}{l} n_i= \hbox{ Nº de repeticiones del valor } x_i \hbox{ } (\Rightarrow \sum_{i=1}^{k} n_i = n) \mathbf{\hbox{ (Frecuencia absoluta)}} \\ f_i= \frac{n_i}{n} \hbox{ } (\Rightarrow \sum_{i=1}^{k} f_i = 1) \mathbf{\hbox{ (Frecuencia relativa)}} \\ N_i = \sum_{j=1}^{i} n_j \mathbf{\hbox{ (Frecuencia absoluta acumulada)}} \\ F_i = \frac{N_i}{n} = \sum_{j=1}^{i} f_j \mathbf{\hbox{ (Frecuencia relativa acumulada)}} \end{array}\right.$$

Datos agrupados en intervalos, $n < 50$

$$\left\{\begin{array}{l} R = Valor_{máximo}-Valor_{mínimo} \mathbf{\hbox{ (Rango o recorrido) }}\\ N = \sqrt{n} \mathbf{\hbox{ (Nº intervalos, aproximando a las unidades por defecto) }}\\ a = \frac{R}{N} \mathbf{\hbox{ (Amplitud, aproximando a las unidades por exceso) }}\\ I_i = [l_i,L_i) \mathbf{\hbox{ (Intervalos no solapados que cubren todo el rango de datos) }}\\ L_i=l_i + a \mathbf{\hbox{ (Extremo superior del intervalo) }}\\ l_1= Valor_{mínimo} - \left( \frac{a \cdot N - R}{2}\right) \mathbf{\hbox{ (Extremo inferior del primer intervalo) }}\\ x_i = \frac{l_i+L_i}{2} \mathbf{\hbox{ (Marca de clase) }} \\ \end{array}\right.$$

Datos agrupados en intervalos, $n \geq 50$

$$\left\{\begin{array}{l} R = Valor_{máximo}-Valor_{mínimo} \mathbf{\hbox{ (Rango o recorrido) }}\\ p = 1+ log_{2} (n) = \frac{log(n)}{log(2)} = 1 + 3.332 \cdot log (n) \mathbf{\hbox{ (aproximando a las unidades por defecto) }}\\ N=\left\{\begin{array}{l} p & si & \hbox{p es impar}\\ p+1 & si & \hbox{p es par}\\ \end{array}\right. \mathbf{\hbox{ (Nº intervalos. Fórmula de Sturges) }}\\ a = \frac{R}{N} \mathbf{\hbox{ (Amplitud, aproximando a las unidades por exceso) }}\\ I_i = [l_i,L_i) \mathbf{\hbox{ (Intervalos no solapados que cubren todo el rango de datos) }}\\ L_i=l_i + a \mathbf{\hbox{ (Extremo superior del intervalo) }}\\ l_1= Valor_{mínimo} - \left( \frac{a \cdot N - R}{2}\right) \mathbf{\hbox{ (Extremo inferior del primer intervalo) }}\\ x_i = \frac{l_i+L_i}{2} \mathbf{\hbox{ (Marca de clase) }} \\ \end{array}\right.$$

Representación gráfica

$$\mathbf{\hbox{Variables}} \left\{\begin{array}{l} \mathbf{\hbox{Cuantitativa discreta y cualitativa}} & \longrightarrow & \left\{\begin{array}{l} \mathbf{\hbox{Diagrama de barras (y polígono de frecuencias)}}\\ \mathbf{\hbox{Diagrama de sectores}}\\ \end{array}\right.\\ \mathbf{\hbox{Cuantitativa continua}} & \longrightarrow & \begin{array}{l} \mathbf{\hbox{Histograma (y polígono de frecuencias)}}\\ \end{array}\\ \end{array}\right.$$

Medidas de centralización

$$\left\{\begin{array}{l} \mathbf{\hbox{ (Media) }} & \bar{x} = \frac{\sum_{i=1}^{n} x_i}{n} = \frac{\sum_{i=1}^{k} x_i \cdot n_i}{n}\\ \mathbf{\hbox{ (Moda) }} & \left\{\begin{array}{l} \mathbf{\hbox{ Datos no agrupados }} \left.\begin{array}{l} Mo = x_i, \hbox{ dato con mayor frecuencia absoluta } n_i\\ \end{array}\right.\\ \mathbf{\hbox{ Datos agrupados }} \left\{\begin{array}{l} \mathbf{\hbox{ (Intervalo modal) }} I_i=[l_i,L_i), \hbox{ con mayor frecuencia absoluta } n_i\\ Mo = l_i+\frac{n_i-n_{i-1}}{2n_i-n_{i-1}-n_{i+1}}(L_i - l_i)\\ \end{array}\right.\\ \end{array}\right.\\ \mathbf{\hbox{ (Mediana) }} & \left\{\begin{array}{l} Me = \hbox{ Valor que deja por debajo el 50% de los datos}\\ \mathbf{\hbox{ Datos no agrupados }} Me = \left\{\begin{array}{l} \frac{x_i+x_{i+1}}{2} & si & N_{i-1} < \frac{n}{2} = N_{i}\\ x_{i} & si & \frac{n}{2} < N_{i}\\ \end{array}\right.\\ \mathbf{\hbox{ Datos agrupados }} \left\{\begin{array}{l} \mathbf{\hbox{ (Intervalo mediano) }} I_i=[l_i,L_i) & si & N_{i-1} < \frac{n}{2} \leq N_{i}\\ Me = l_i+\frac{\frac{n}{2}-N_{i-1}}{n_i}(L_i - l_i) & & \\ \end{array}\right.\\ \end{array}\right. \end{array}\right.$$

Medidas de posición

$$\left\{\begin{array}{l} \mathbf{\hbox{ (Cuantil) }} & \hbox{Valor que deja por debajo el } \frac{100 \cdot r}{k} \hbox{% de los datos, } r=1,\cdots,k-1\\ \mathbf{\hbox{ (Cuartil) }} k=4,r=1,2,3 & \left\{\begin{array}{l} \mathbf{\hbox{ Datos no agrupados }} Q_r = \left\{\begin{array}{l} \frac{x_i+x_{i+1}}{2} & si & N_{i-1} < \frac{r \cdot n}{4} = N_{i}\\ x_{i} & si & \frac{r \cdot n}{4} < N_{i}\\ \end{array}\right.\\ \mathbf{\hbox{ Datos agrupados }} \left\{\begin{array}{l} \mathbf{\hbox{ (Intervalo del cuartil) }} I_i=[l_i,L_i) & si & N_{i-1} < \frac{r \cdot n}{4} \leq N_{i}\\ Q_r = l_i+\frac{\frac{r \cdot n}{4}-N_{i-1}}{n_i}(L_i - l_i) & & \\ \end{array}\right.\\ \end{array}\right.\\ \mathbf{\hbox{ (Decil) }} k=10, r=1,\cdots,9 & \left\{\begin{array}{l} \mathbf{\hbox{ Datos no agrupados }} D_r = \left\{\begin{array}{l} \frac{x_i+x_{i+1}}{2} & si & N_{i-1} < \frac{r \cdot n}{10} = N_{i}\\ x_{i} & si & \frac{r \cdot n}{10} < N_{i}\\ \end{array}\right.\\ \mathbf{\hbox{ Datos agrupados }} \left\{\begin{array}{l} \mathbf{\hbox{ (Intervalo del decil) }} I_i=[l_i,L_i) & si & N_{i-1} < \frac{r \cdot n}{10} \leq N_{i}\\ D_r = l_i+\frac{\frac{r \cdot n}{10}-N_{i-1}}{n_i}(L_i - l_i) & & \\ \end{array}\right.\\ \end{array}\right.\\ \mathbf{\hbox{ (Centil) }} k=100, r=1,\cdots,99 & \left\{\begin{array}{l} \mathbf{\hbox{ Datos no agrupados }} P_r = \left\{\begin{array}{l} \frac{x_i+x_{i+1}}{2} & si & N_{i-1} < \frac{r \cdot n}{100} = N_{i}\\ x_{i} & si & \frac{r \cdot n}{100} < N_{i}\\ \end{array}\right.\\ \mathbf{\hbox{ Datos agrupados }} \left\{\begin{array}{l} \mathbf{\hbox{ (Intervalo del centil) }} I_i=[l_i,L_i) & si & N_{i-1} < \frac{r \cdot n}{100} \leq N_{i}\\ P_r = l_i+\frac{\frac{r \cdot n}{100}-N_{i-1}}{n_i}(L_i - l_i) & & \\ \end{array}\right.\\ \end{array}\right.\\ \end{array}\right.$$

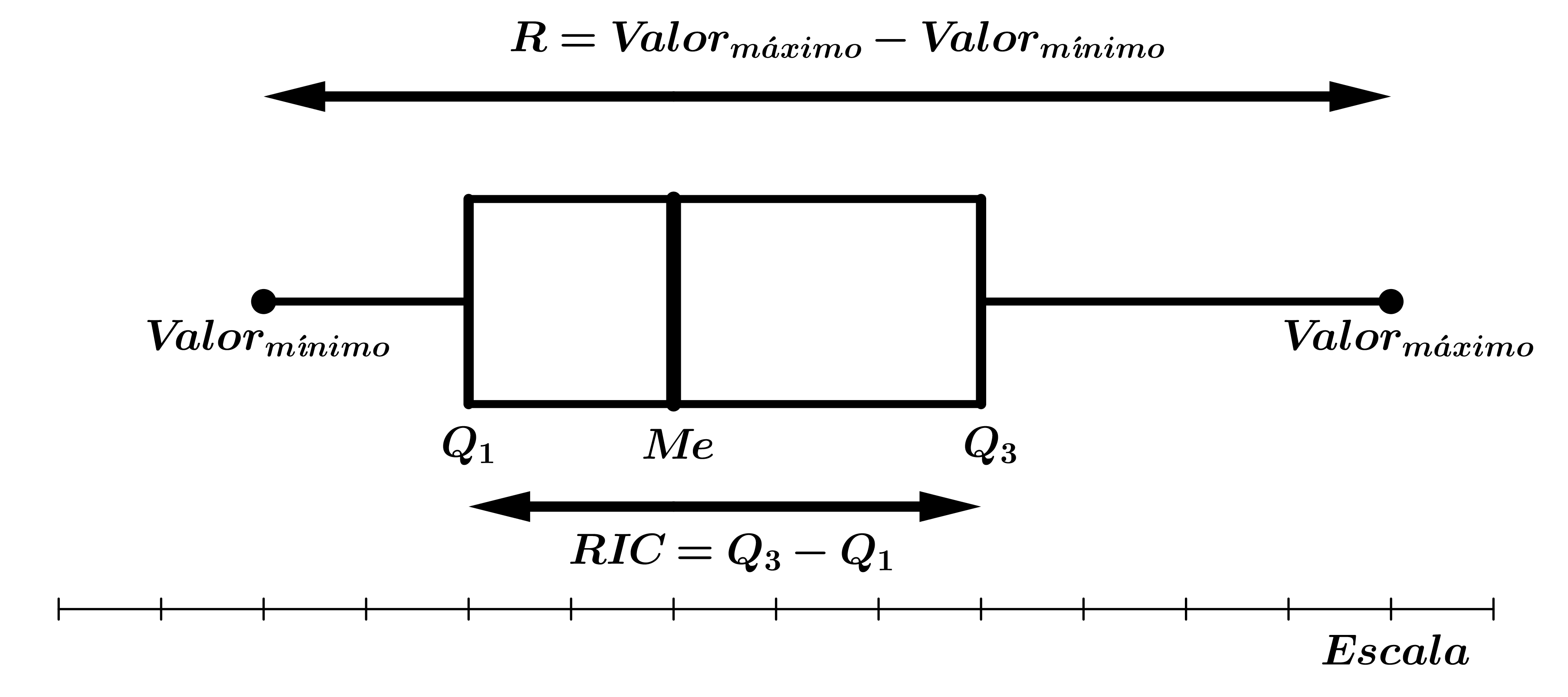
Medidas de dispersión

$$\left\{\begin{array}{l} \mathbf{\hbox{ (Rango o recorrido) }} & R = Valor_{máximo} - Valor_{mínimo}\\ \mathbf{\hbox{ (Rango intercuartílico) }} & RIC = Q_3 - Q_1\\ \mathbf{\hbox{ (Desviación media) }} & D_m = \frac{\sum_{i=1}^{k} |x_i - \bar{x}| \cdot n_i}{n}\\ \mathbf{\hbox{ (Varianza) }} & V = \sigma^{2} = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n} = \frac{\sum_{i=1}^{k} x_i^2 \cdot n_i}{n} - \bar{x}^2\\ \mathbf{\hbox{ (Desviación típica) }} & \sigma = \sqrt{V}\\ \mathbf{\hbox{ (Coeficiente de variación de Pearson) }} & CV = \frac{\sigma}{|\bar{x}|} \cdot 100 \mathbf{\hbox{ (%) }}\\ \end{array}\right.$$

Diagrama de Cajas y bigotes