INTEGRALES (FORMULARIOS)
Integrales:
Integral indefinida. Integrales inmediatas
Dada una función \(f(x)\) continua, se define una primitiva (o integral) de \(f(x)\), como una función \(F(x)\) tal que \(F'(x)=f(x)\).
En ese caso, decimos que \(F(x)=\displaystyle{\int{f(x) dx}} + C\), donde \( C \in \mathbb{R} \) (Notación de Leibnitz)
$$ \left\{\begin{array}{l} \displaystyle{\int{k dx}} = kx + C\\ \displaystyle{\int{x^{n} dx}} = \displaystyle{\frac{x^{n+1}}{n+1}} + C, (n \neq -1)\\ \displaystyle{\int{\frac{1}{x} dx}} = Ln|x| + C\\ \displaystyle{\int{e^{x} dx}} = e^{x} + C\\ \displaystyle{\int{a^{x} dx}} = \displaystyle{\frac{a^{x}}{Ln|a|}} + C\\ \displaystyle{\int{cos(x) dx}} = sen(x) + C\\ \displaystyle{\int{sen(x) dx}} = -cos(x) + C\\ \displaystyle{\int{\left(1+tg^2(x)\right) dx}} = \displaystyle{\int{\frac{1}{cos^2(x)} dx}} = tg(x) + C\\ \displaystyle{\int{\left(1+cotg^2(x)\right) dx}} = \displaystyle{\int{\frac{1}{sen^2(x)} dx}} = -cotg(x) + C\\ \displaystyle{\int{\frac{1}{\sqrt[]{1-x^2}} dx}} = arcsen(x) + C\\ \displaystyle{\int{\frac{1}{1+x^2} dx}} = arctg(x) + C\\ \end{array}\right. $$Métodos de Integración: Integral de formas compuestas (Cambio de variable)
$$ \left\{\begin{array}{l} \displaystyle{\int{u'(x) (u(x))^{n} dx}} = \displaystyle{\frac{(u(x))^{n+1}}{n+1}} + C, (n \neq -1)\\ \displaystyle{\int{\frac{u'(x)}{u(x)} dx}} = Ln|u(x)| + C\\ \displaystyle{\int{u'(x) e^{u(x)} dx}} = e^{u(x)} + C\\ \displaystyle{\int{u'(x) a^{u(x)} dx}} = \displaystyle{\frac{a^{u(x)}}{Ln|a|}} + C\\ \displaystyle{\int{u'(x) cos(u(x)) dx}} = sen(u(x)) + C\\ \displaystyle{\int{u'(x) sen(u(x)) dx}} = -cos(u(x)) + C\\ \displaystyle{\int{u'(x)\left(1+tg^2(u(x))\right) dx}} = \displaystyle{\int{\frac{u'(x)}{cos^2(u(x))} dx}} = tg(u(x)) + C\\ \displaystyle{\int{u'(x)\left(1+cotg^2(u(x))\right) dx}} = \displaystyle{\int{\frac{u'(x)}{sen^2(u(x))} dx}} = -cotg(u(x)) + C\\ \displaystyle{\int{\frac{u'(x)}{\sqrt[]{1-u^2(x)}} dx}} = arcsen(u(x)) + C\\ \displaystyle{\int{\frac{u'(x)}{1+u^2(x)} dx}} = arctg(u(x)) + C\\ \end{array}\right. $$Linealidad de la integral
$$ \left.\begin{array}{ll} \displaystyle{\int{\left(\alpha f(x) \pm \beta g(x)\right)dx}}=\displaystyle{\alpha\int{f(x)dx}} \pm \displaystyle{\beta\int{g(x)dx}} & \alpha, \beta \in \mathbb{R}\\ \end{array}\right. $$Método de integración integración por partes
Sean \(f(x)\), \(g(x)\) continuas en \([a,b]\). Sea \(G(x)\) una primitiva de \(g(x)\):
$$ \displaystyle{\int{f(x)g(x)dx}}=f(x)G(x)-\displaystyle{\int{f'(x)G(x)dx}} $$Integral definida
Sea \(f(x)\) una función continua en un intervalo \([a,b]\) y \(F(x)\) una primitiva de \(f(x)\). La integral definidia de \(f(x)\) en el intervalo \([a,b]\) se denota por \(\displaystyle{\int_{a}^{b}{f(x)dx}}.\)
Propiedades:
-
Regla de Barrow:
\(\displaystyle{\int_{a}^{b}{f(x)dx}}={\left[F(x)\right]}_{x=a}^{x=b}=F(b)-F(a)\)
-
\(\displaystyle{\int_{a}^{b}{f(x)dx}} \in \mathbb{R}\), no depende de la primitiva \(F(x)\) (la constante C se elimina al restar).
-
\(\displaystyle{\int_{a}^{b}{f(x)dx}}=-\displaystyle{\int_{b}^{a}{f(x)dx}}\)
-
Aditividad en el intervalo:
Sea \(f(x)\) continua en \([a,b]\), \(c \in [a,b] \Rightarrow \displaystyle{\int_{a}^{b}{f(x)dx}}=\displaystyle{\int_{a}^{c}{f(x)dx}}+\displaystyle{\int_{c}^{b}{f(x)dx}}\)
-
Monotonía en el intervalo:
Sean \(f(x)\), \(g(x)\) continuas en \([a,b]\), \(f(x) \leq g(x), x \in [a,b],\) $$\Rightarrow \displaystyle{\int_{a}^{b}{f(x)dx}} \leq \displaystyle{\int_{a}^{b}{g(x)dx}}$$
Interpretación geométrica de la integral definida de una función en un intervalo cerrado
La integral definida coincide con el área sólo cuando la función es positiva, es decir, está por encima del \(\hbox{eje X}\). Cuando la función es negativa, la integral también es negativa, dándonos el área cambiada de signo. Y cuando la función cambia de signo, es decir, está por encima y por debajo del \(\hbox{eje X}\), la integral es igual a la resta entre las áreas de las regiones superiores y las áreas de las regiones inferiores.


Área encerrada entre una curva y el eje X
-
Resolvemos la ecuación \(f(x)=0\). Supongamos que los ceros obtenidos en el intervalo \([a,b]\), ordenados de menor a mayor, son \(x=x_1,x_2,\cdots,x_n.\)
-
Calculamos las integrales: \(\displaystyle{\int_{a}^{x_1}{f(x)dx}},\displaystyle{\int_{x_1}^{x_2}{f(x)dx}}, \cdots, \displaystyle{\int_{x_n}^{b}{f(x)dx}}.\)
-
El área es la suma de los valores absolutos de cada una de las integrales anteriores.

Área encerrada entre dos curvas
Dadas las funciones \(f(x)\) y \(g(x)\), \(f(x) \geq g(x)\), para calcular el área del recinto delimitado por las curvas \(y=f(x)\) e \(y=g(x)\):
-
Resolvemos la ecuación \(f(x)=g(x)\). Supongamos que los ceros obtenidos, ordenados de menor a mayor, son \(x=a\) y \(x=b\).
-
Calculamos la integral: \(\displaystyle{\int_{a}^{b}{\left(f(x)-g(x)\right)dx}}\).
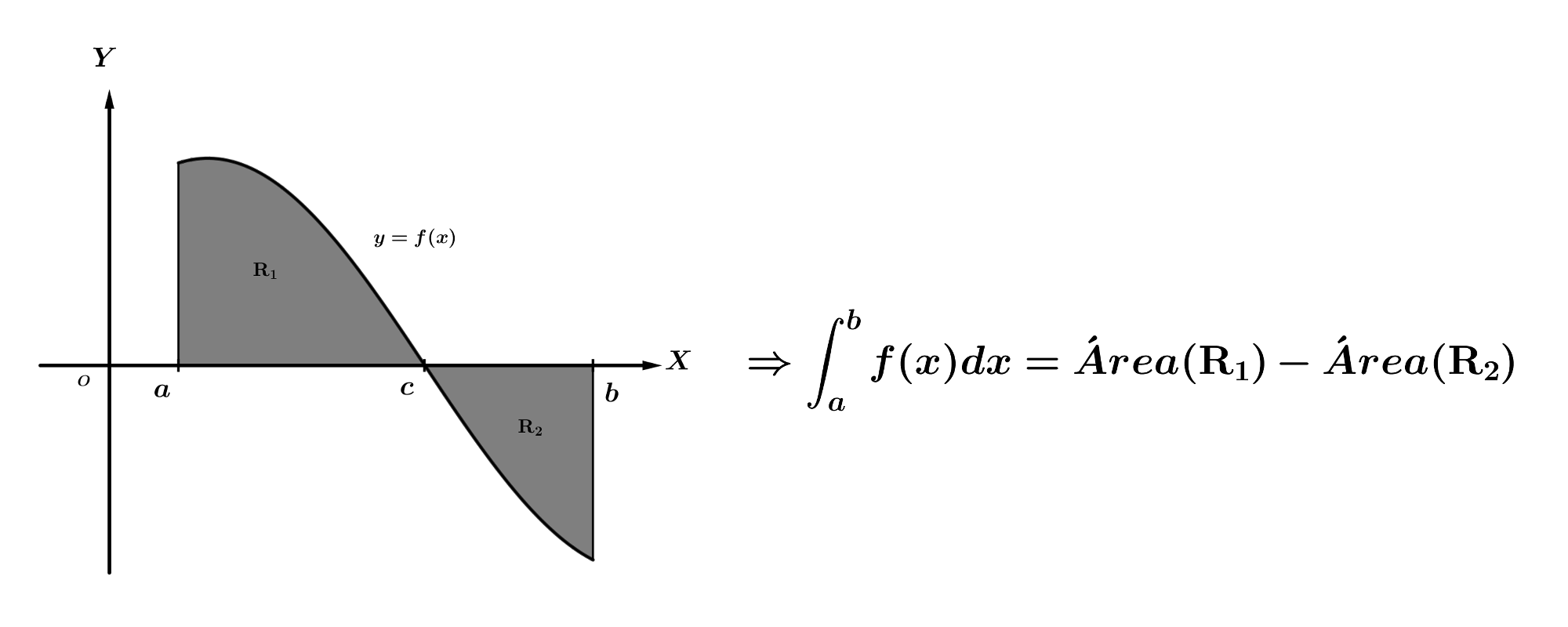
Aplicando la linealidad de la integral y teniendo en cuenta que \(\displaystyle{\int_{a}^{b}{f(x)dx}}=Área(\mathbf{R_1})\) y \(\displaystyle{\int_{a}^{b}{g(x)dx}}=Área(\mathbf{R_2})\):
$$Área(\mathbf{R})=\displaystyle{\int_{a}^{b}{\left(f(x)-g(x)\right)dx}}=\displaystyle{\int_{a}^{b}{f(x)dx}}-\displaystyle{\int_{a}^{b}{g(x)dx}}=$$ $$=Área(\mathbf{R_1})-Área(\mathbf{R_2})$$

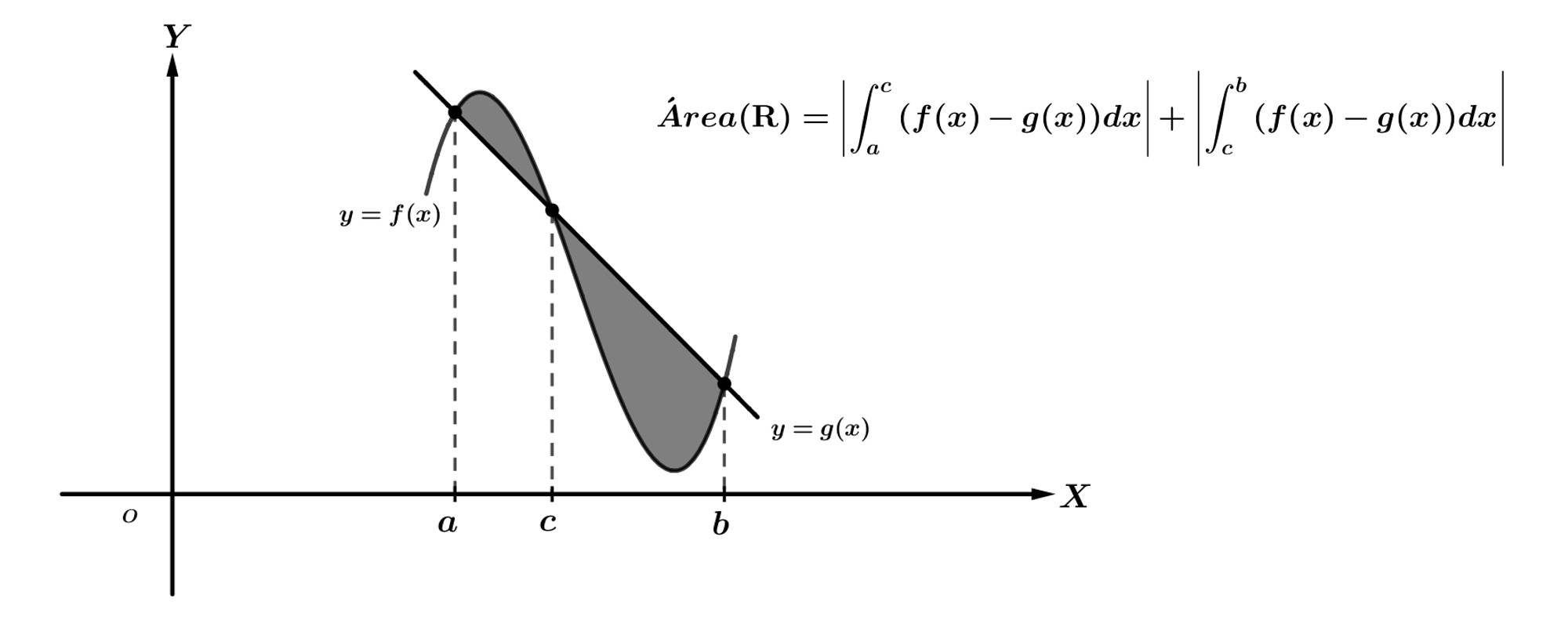
En general, para calcular el área del recinto delimitado por las curvas \(y=f(x)\) e \(y=g(x)\):
-
Resolvemos la ecuación \(f(x)=g(x)\). Supongamos que los ceros obtenidos, ordenados de menor a mayor, son \(x=a,x=c\) y \(x=b\).
-
Calculamos las integrales: \(\displaystyle{\int_{a}^{c}{\left(f(x)-g(x)\right)dx}}\) y \(\displaystyle{\int_{c}^{b}{\left(f(x)-g(x)\right)dx}}\).
-
El área es la suma de los valores absolutos de las integrales anteriores (de ese modo no hay que tener en cuenta qué función es mayor y menor en cada intervalo).