2ºBACH CCSS INTEGRALES (ACTIVIDADES)

Actividades: Integral indefinida y definida. Aplicaciones de la integral

Actividad (#1)

Obtén una función cuya derivada sea:

1. \(f(x)=1\)
2. \(f(x)=3x^2+1\)
3. \(f(x)=cos(x)-1\)
4. \(f(x)=3e^{x}-x^2\)
5. \(f(x)=\displaystyle{\frac{2}{x}}\), si \(x>0\)

Solución:

1. \(F(x)=\displaystyle{\int{1dx}}=x+C\)
2. \(F(x)=\displaystyle{\int{(3x^2+1)dx}}=x^3+x+C\)
3. \(F(x)=\displaystyle{\int{(cos(x)-1)dx}}=sen(x)-x+C\)
4. \(F(x)=\displaystyle{\int{(3e^{x}-x^2)dx}}=3e^{x}-\displaystyle{\frac{x^3}{3}}+C\)
5. \(F(x)=\displaystyle{\int{\frac{2}{x}}dx}=2Ln(x)+C\), si \(x > 0\)

Actividad (#2)

Halla una primitiva de la función \(y=2x-1\) que corta al eje de abscisas para \(x=-1\).

Solución:

\(F(x)=\displaystyle{\int{(2x-1)dx}}=x^2-x-2\)

Actividad (#3)

Obtén una primitiva de las siguientes funciones:

1. \(f(x)=x-1\) que pasa por \(P(2,1)\).
2. \(f(x)=x-e^{x}\) que pasa por el origen de coordenadas.
3. \(f(x)=3x^2+2x+1\) que se anula para \(x=1\).

Solución:

1. \(F(x)=\displaystyle{\int{(x-1)dx}}=\displaystyle{\frac{x^2}{2}}-x+1\)
2. \(F(x)=\displaystyle{\int{(x-e^{x})dx}}=\displaystyle{\frac{x^2}{2}}-e^{x}+1\)
3. \(F(x)=\displaystyle{\int{(3x^2+2x+1)dx}}=x^3+x^2+x-3\)

Actividad (#4)

Obtén la primitiva de la función \(y=x^2-sen(x)\) que pasa por el origen de coordenadas.

Solución:

\(F(x)=\displaystyle{\int{(x^2-sen(x))dx}}=\displaystyle{\frac{x^3}{3}}+cos(x)-1\)

Actividad (#5)

Obtén la expresión de una función \(f\) tal que \(f'(x)=x^2+2e^{x}\) sabiendo que se anula para \(x=0\).

Solución:

\(f(x)=\displaystyle{\int{f'(x)dx}}=\displaystyle{\frac{x^3}{3}}+2e^{x}-2\)

Actividad (#6)

Obtén \(f(x)\) sabiendo que tiene un extremo relativo en el punto \((-1,1)\) y que su derivada segunda viene dada por \(f''(x)=6x-12\).

Solución:

\(f(x)=x^3-6x^2-15x-7\)

Actividad (#7)

Determina la función \(f: \mathbb{R} \rightarrow \mathbb{R}\) que para \(x=1\) tiene de tangente a \(x+12y=13\) y tal que \(f''(x)=x^2-1\).

Solución:

\(f(x)=\displaystyle{\frac{x^4}{12}}-\displaystyle{\frac{x^2}{2}}+\displaystyle{\frac{7x}{12}}+\displaystyle{\frac{5}{6}}\)

Actividad (#8)

Obtén la primitiva de la función \(f: \mathbb{R} \rightarrow \mathbb{R}\) con \(f(x)= \left\{\begin{array}{lcc} 2x & si & x < 1\\ 2 & si & x \geq 1\\ \end{array}\right.\) que pasa por el punto \(P(1,4)\).

Solución:

\(F(x)= \left\{\begin{array}{lcc} x^2+3 & si & x < 1\\ 2x+2 & si & x \geq 1\\ \end{array}\right.\)

Actividad (#9)

Obtén \(\displaystyle{\int{\left|2x-2\right|dx}}\)

¿Qué primitiva pasa por el origen de coordenadas?

Solución:

\(F(x)= \left\{\begin{array}{lcc} x^2-2x+2 & si & x \geq 1\\ -x^2+2x & si & x < 1\\ \end{array}\right.\)

Actividad (#10)

Obtén las siguientes integrales indefinidas:

1. \(\displaystyle{\int{5dx}}\)
2. \(\displaystyle{\int{xdx}}\)
3. \(\displaystyle{\int{\frac{1}{x^2}dx}}\)
4. \(\displaystyle{\int{\frac{1}{x}dx}}\)
5. \(\displaystyle{\int{x^3dx}}\)
6. \(\displaystyle{\int{\sqrt[4]{x^5}dx}}\)
7. \(\displaystyle{\int{\sqrt[3]{x^2}dx}}\)
8. \(\displaystyle{\int{\frac{1}{\sqrt[3]{x^5}}}dx}\)

Solución:

Para resolver cada una de las siguinetes integrales, debemos escribir cada una de las funciones como una potencia de base \(x\):

1. \(\displaystyle{\int{5dx}}=5x+C\)
2. \(\displaystyle{\int{xdx}}=\displaystyle{\frac{x^2}{2}}+C\)
3. \(\displaystyle{\int{\frac{1}{x^2}dx}}=\displaystyle{\frac{-1}{x}}+C\)
4. \(\displaystyle{\int{\frac{1}{x}dx}}=Ln\left|x\right|+C\)
5. \(\displaystyle{\int{x^3dx}}=\displaystyle{\frac{x^{4}}{4}}+C\)
6. \(\displaystyle{\int{\sqrt[4]{x^5}dx}}=\displaystyle{\frac{4x^2\sqrt[4]{x}}{9}}+C\)
7. \(\displaystyle{\int{\sqrt[3]{x^2}dx}}=\displaystyle{\frac{3x\sqrt[3]{x^2}}{5}}+C\)
8. \(\displaystyle{\int{\frac{1}{\sqrt[3]{x^5}}}dx}=\displaystyle{\frac{-3}{2\sqrt[3]{x^2}}}+C\)

Actividad (#11)

Halla las primitivas de los siguientes polinomios:

1. \(f(x)=x^4+4x^3-5x+2\)
2. \(f(x)=3x^3+x^2-7x\)
3. \(f(x)=3x^6+4x^2-1\)
4. \(f(x)=4x^5+3x^4-2x^3+6x^2-9\)
5. \(f(x)=ax^2+bx+c\)

Solución:

1. \(\displaystyle{\int{\left(x^4+4x^3-5x+2\right)dx}}=\displaystyle{\frac{x^5}{5}}+x^4-\displaystyle{\frac{5x^2}{2}}+2x+C\)
2. \(\displaystyle{\int{\left(3x^3+x^2-7x\right)dx}}=\displaystyle{\frac{3x^4}{4}}+\displaystyle{\frac{x^3}{3}}-\displaystyle{\frac{7x^2}{2}}+C\)
3. \(\displaystyle{\int{\left(3x^6+4x^2-1\right)dx}}=\displaystyle{\frac{3x^7}{7}}+\displaystyle{\frac{4x^3}{3}}-x+C\)
4. \(\displaystyle{\int{\left(4x^5+3x^4-2x^3+6x^2-9\right)dx}}=\displaystyle{\frac{2x^6}{3}}+\displaystyle{\frac{3x^5}{5}}-\displaystyle{\frac{x^4}{2}}+2x^3-9x+C\)
5. \(\displaystyle{\int{\left(ax^2+bx+c\right)dx}}=\displaystyle{\frac{ax^3}{3}}+\displaystyle{\frac{bx^2}{2}}+cx+C\)

Actividad (#12)

Obtén las siguientes integrales indefinidas:

1. \(\displaystyle{\int{\left(x^2-e^{x}\right)dx}}\)
2. \(\displaystyle{\int{\left(\frac{2}{x^4}-x^4\right)dx}}\)
3. \(\displaystyle{\int{\left(1-\frac{3}{x^5}\right)dx}}\)
4. \(\displaystyle{\int{\left(x-\frac{2}{x}\right)dx}}\)
5. \(\displaystyle{\int{\left(3x-2sen(x)\right)dx}}\)
6. \(\displaystyle{\int{\left(3e^x-cos(x)\right)dx}}\)

Solución:

1. \(\displaystyle{\int{\left(x^2-e^{x}\right)dx}}=\displaystyle{\frac{x^3}{3}}-e^{x}+C\)
2. \(\displaystyle{\int{\left(\frac{2}{x^4}-x^4\right)dx}}=\displaystyle{-\frac{2}{3x^3}}-\displaystyle{\frac{x^{5}}{5}}+C\)
3. \(\displaystyle{\int{\left(1-\frac{3}{x^5}\right)dx}}=x+\displaystyle{\frac{3}{4x^4}}+C\)
4. \(\displaystyle{\int{\left(x-\frac{2}{x}\right)dx}}=\displaystyle{\frac{x^{2}}{2}}-2Ln\left|x\right|+C\)
5. \(\displaystyle{\int{\left(3x-2sen(x)\right)dx}}=\displaystyle{\frac{3x^{2}}{2}}+2cos(x)+C\)
6. \(\displaystyle{\int{\left(3e^x-cos(x)\right)dx}}=3e^{x}-sen(x)+C\)

Actividad (#13)

Descomponiendo en sumandos las fracciones obtén:

1. \(\displaystyle{\int{\frac{x-3}{x}dx}}\)
2. \(\displaystyle{\int{\frac{x^2-5x+1}{x}dx}}\)
3. \(\displaystyle{\int{\frac{x^2-3x+1}{x^2}dx}}\)
4. \(\displaystyle{\int{\frac{x^3-3x^2+x-5}{2x^3}dx}}\)
5. \(\displaystyle{\int{\frac{\sqrt[]{x}-2x}{x^2}dx}}\)
6. \(\displaystyle{\int{\frac{3x}{x+4}dx}}\)

Solución:

1. \(\displaystyle{\int{\frac{x-3}{x}dx}}=x+3Ln\left|x\right|+C\)
2. \(\displaystyle{\int{\frac{x^2-5x+1}{x}dx}}=\displaystyle{\frac{x^2}{2}}-5x+Ln\left|x\right|+C\)
3. \(\displaystyle{\int{\frac{x^2-3x+1}{x^2}dx}}=x-3Ln\left|x\right|-\displaystyle{\frac{1}{x}}+C\)
4. \(\displaystyle{\int{\frac{x^3-3x^2+x-5}{2x^3}dx}}=\displaystyle{\frac{1}{2}}x-\displaystyle{\frac{3}{2}}Ln\left|x\right|-\displaystyle{\frac{1}{2x}}+\displaystyle{\frac{5}{4x^{2}}}+C\)
5. \(\displaystyle{\int{\frac{\sqrt[]{x}-2x}{x^2}dx}}=-\displaystyle{\frac{2}{\sqrt[]{x}}}-2Ln\left|x\right|+C\)
6. \(\displaystyle{\int{\frac{3x}{x+4}dx}}=3x-12Ln\left|x-4\right|+C\)

Actividad (#14)

Obtén las siguientes integrales logarítmicas:

1. \(\displaystyle{\int{\frac{1}{x-2}dx}}\)
2. \(\displaystyle{\int{\frac{x^2}{x^3-8}dx}}\)
3. \(\displaystyle{\int{\frac{e^{x}-2x}{e^{x}-x^2+5}dx}}\)
4. \(\displaystyle{\int{\frac{cos(x)-sen(x)}{sen(x)+cos(x)}dx}}\)

Solución:

1. \(\displaystyle{\int{\frac{1}{x-2}dx}}=Ln\left|x-2\right|+C\)
2. \(\displaystyle{\int{\frac{x^2}{x^3-8}dx}}=\displaystyle{\frac{1}{3}}Ln\left|x^3-8\right|+C\)
3. \(\displaystyle{\int{\frac{e^{x}-2x}{e^{x}-x^2+5}dx}}=Ln\left|e^{x}-x^2+5\right|+C\)
4. \(\displaystyle{\int{\frac{cos(x)-sen(x)}{sen(x)+cos(x)}dx}}=Ln\left|sen(x)+cos(x)\right|+C\)

Actividad (#15)

Obtén las siguientes integrales de formas compuestas relacionadas con la función exponencial:

1. \(\displaystyle{\int{e^{3x-2}dx}}\)
2. \(\displaystyle{\int{3x^2 e^{x^3-4}dx}}\)
3. \(\displaystyle{\int{e^{cos(x)}sen(x)dx}}\)
4. \(\displaystyle{\int{(2x-1) e^{x^2-x}dx}}\)

Solución:

1. \(\displaystyle{\int{e^{3x-2}dx}}=\frac{1}{3}e^{3x-2}+C\)
2. \(\displaystyle{\int{3x^2 e^{x^3-4}dx}}=e^{x^3-4}+C\)
3. \(\displaystyle{\int{e^{cos(x)}sen(x)dx}}=-e^{cos(x)}+C\)
4. \(\displaystyle{\int{(2x-1) e^{x^2-x}dx}}=e^{x^2-x}+C\)

Actividad (#16)

Obtén las siguientes integrales de formas compuestas de forma potencial:

1. \(\displaystyle{\int{(3x-2)^3dx}}\)
2. \(\displaystyle{\int{6x(3x^2-2)^5dx}}\)
3. \(\displaystyle{\int{x\sqrt[3]{x^2-1}dx}}\)
4. \(\displaystyle{\int{sen^3(x)cos(x)dx}}\)

Solución:

1. \(\displaystyle{\int{(3x-2)^3dx}}=\displaystyle{\frac{1}{3}} \displaystyle{\frac{(3x-2)^4}{4}}+C\)
2. \(\displaystyle{\int{6x(3x^2-2)^5dx}}=\displaystyle{\frac{(3x^2-2)^6}{6}}+C\)
3. \(\displaystyle{\int{x\sqrt[3]{x^2-1}dx}}=\displaystyle{\frac{3\left(x^2-1\right)\sqrt[3]{x^2-1}}{8}}+C\)
4. \(\displaystyle{\int{sen^3(x)cos(x)dx}}=\displaystyle{\frac{sen^4(x)}{4}}+C\)

Actividad (#17)

Obtén las siguientes integrales de formas compuestas de forma potencial:

1. \(\displaystyle{\int{cos(2x-1)dx}}\)
2. \(\displaystyle{\int{xcos(x^2+1)dx}}\)
3. \(\displaystyle{\int{3x^4sen(x^5)dx}}\)
4. \(\displaystyle{\int{sen(10x)dx}}\)

Solución:

1. \(\displaystyle{\int{cos(2x-1)dx}}=\displaystyle{\frac{1}{2}}sen(2x-1)+C\)
2. \(\displaystyle{\int{xcos(x^2+1)dx}}=\displaystyle{\frac{1}{2}}sen(x^2+1)+C\)
3. \(\displaystyle{\int{3x^4sen(x^5)dx}}=-\frac{3}{5}cos(x^5)+C\)
4. \(\displaystyle{\int{sen(10x)dx}}=-\frac{1}{10}cos(10x)+C\)

Actividad (#18)

Halla la función \(f: \mathbb{R} \rightarrow \mathbb{R}\) sabiendo \(f''(x)=12x-6\) y que la recta tangente a la gráfica de \(f\) en el punto de abscisa \(x=2\) tiene de ecuación \(4x-y-7=0\).

Solución:

\(f(x)=\displaystyle{2x^3}-\displaystyle{3x^2}-\displaystyle{8x}+13\)

Actividad (#19)

Calcula:

1. \(\displaystyle{\int_{0}^{2}{(x^2+x-2)dx}}\)
2. \(\displaystyle{\int_{-1}^{1}{(x^2-1)dx}}\)
3. \(\displaystyle{\int_{1}^{2}{\frac{3}{x+2}dx}}\)
4. \(\displaystyle{\int_{0}^{1}{xe^{x^2}dx}}\)

Solución:

1. \(F(x)=\displaystyle{\int{(x^2+x-2)dx}}=\displaystyle{\frac{2}{3}}\)
2. \(F(x)=\displaystyle{\int{(x^2-1)dx}}=-2\)
3. \(F(x)=\displaystyle{\int{\frac{3}{x+2}dx}}=Ln\left(\displaystyle{\frac{64}{27}}\right)\)
4. \(F(x)=\displaystyle{\int{xe^{x^2}dx}}=\displaystyle{\frac{e-1}{2}}\)

Actividad (#20)

Calcula el área delimitada por la curva \(y=x^3-4x\) con el eje de abscisas en el intervalo \([-1,3]\).

Solución:

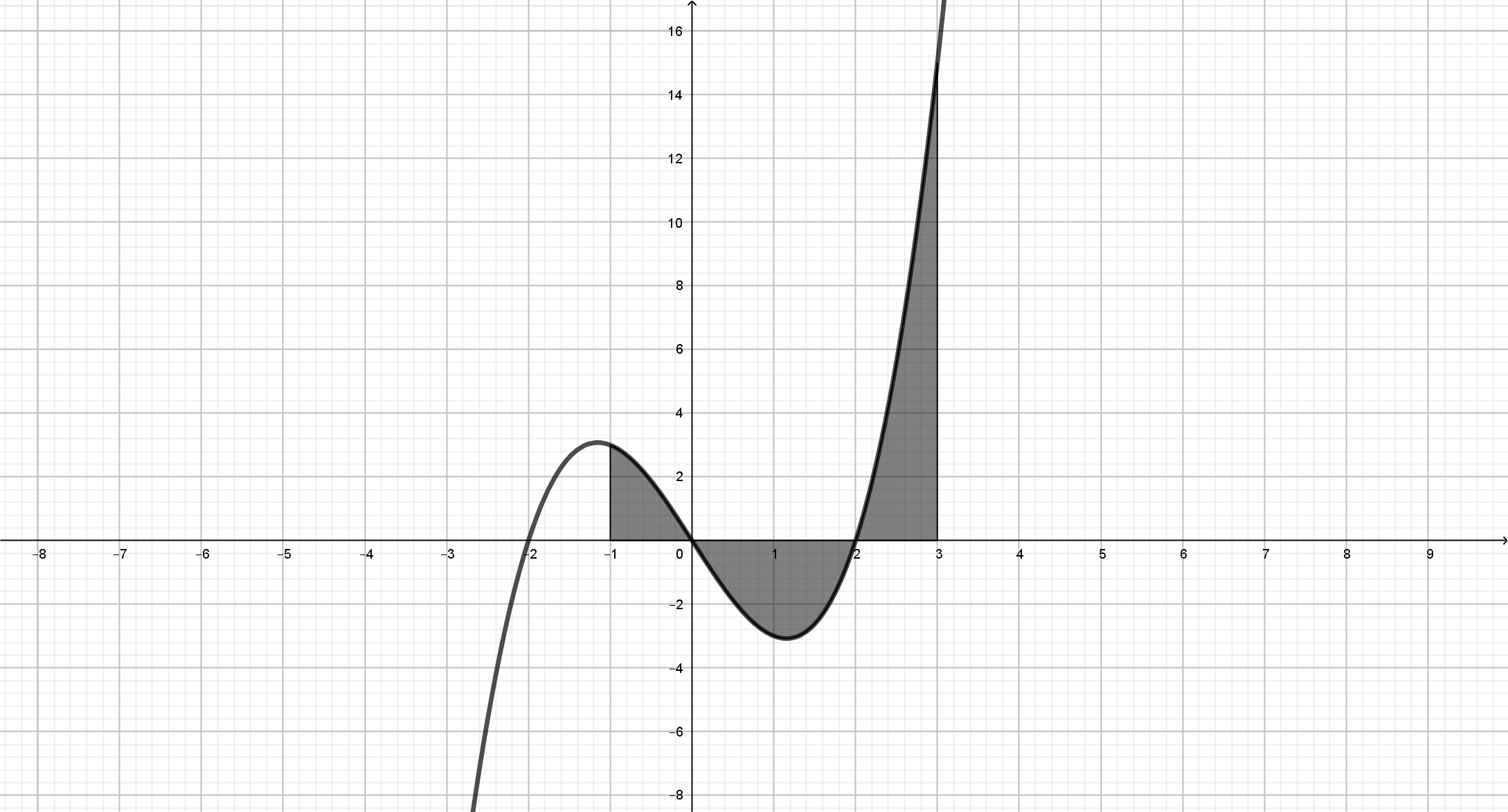
\(Área(\mathbf{R})=Área(\mathbf{R_1})+Área(\mathbf{R_2})+Área(\mathbf{R_3})\)

\(F(x)=\displaystyle{\int{\left(x^3-4x\right)dx}}=\displaystyle{\frac{x^4}{4}}-2x^2+C\)

\(Área(\mathbf{R_1})=\displaystyle{\frac{7}{4}}\)

\(Área(\mathbf{R_2})=4\)

\(Área(\mathbf{R_3})=\displaystyle{\frac{25}{4}}\)

\(Área(\mathbf{R})=12\)