PROGRAMACIÓN LINEAL (FORMULARIOS)
Inecuaciones lineales
$$\mathbf{\hbox{Rectas oblicuas}}$$ $$\left\{\begin{array}{l} y \leq ax+b \mathbf{\hbox{ semiplano inferior a }} y=ax+b \mathbf{\hbox{ (incluida la recta)}}\\ y < ax+b \mathbf{\hbox{ semiplano inferior a }} y=ax+b \mathbf{\hbox{ (sin incluir la recta)}}\\ y \geq ax+b \mathbf{\hbox{ semiplano superior a }} y=ax+b \mathbf{\hbox{ (incluida la recta)}}\\ y > ax+b \mathbf{\hbox{ semiplano superior a }} y=ax+b \mathbf{\hbox{ (sin incluir la recta)}}\\ \end{array}\right.$$ $$\mathbf{\hbox{Rectas verticales}}$$ $$\left\{\begin{array}{l} x \leq c \mathbf{\hbox{ semiplano izquierdo a }} x=c \mathbf{\hbox{ (incluida la recta)}}\\ x < c \mathbf{\hbox{ semiplano izquierdo a }} x=c \mathbf{\hbox{ (sin incluir la recta)}}\\ x \geq c \mathbf{\hbox{ semiplano derecho a }} x=c \mathbf{\hbox{ (incluida la recta)}}\\ x > c \mathbf{\hbox{ semiplano derecho a }} x=c \mathbf{\hbox{ (sin incluir la recta)}}\\ \end{array}\right.$$ $$\mathbf{\hbox{Rectas horizontales}}$$ $$\left\{\begin{array}{l} y \leq d \mathbf{\hbox{ semiplano inferior a }} y=d \mathbf{\hbox{ (incluida la recta)}}\\ y < d \mathbf{\hbox{ semiplano inferior a }} y=d \mathbf{\hbox{ (sin incluir la recta)}}\\ y \geq d \mathbf{\hbox{ semiplano superior a }} y=d \mathbf{\hbox{ (incluida la recta)}}\\ y > d \mathbf{\hbox{ semiplano superior a }} y=d \mathbf{\hbox{ (sin incluir la recta)}}\\ \end{array}\right.$$Nota: Recuerda que en una inecuación, al multiplicar o dividir por un número negativo, la desigualdad cambia de sentido.
Sistemas de Inecuaciones lineales
Para resolver un sistema de inecuaciones lineales, debemos representar cada uno de los semiplanos determinados por las restricciones y determinar el conjunto de puntos (o recinto) en el que se verifican todas y cada una de las restricciones a la vez. Esa región puede ser vacía, acotada o no acotada.
Para saber si un punto del plano \(P(x_0,y_0)\) pertenece al semiplano determinado por la inecuación \(\Pi_{-}:ax+by+c < 0\), al semiplano contrario \((\Pi_{+}:ax+by+c > 0) \) o a la recta \(r:ax+by+c = 0\), sustituimos las coordenadas del punto en la correspondiente ecuación o inecuación y comprobamos cuál de ellas se verifica. $$\left\{\begin{array}{l} \hbox{Si } ax_0+by_0+c < 0 \rightarrow P(x_0,y_0) \in \Pi_{-}\\ \\ \hbox{Si } ax_0+by_0+c = 0 \rightarrow P(x_0,y_0) \in r\\ \\ \hbox{Si } ax_0+by_0+c > 0 \rightarrow P(x_0,y_0) \in \Pi_{+}\\ \end{array}\right.$$
Problemas de Programación Lineal
En los problemas de programación lineal con dos variables x, y, pretendemos optimizar (maximizar o minimizar) una expresión denominada función objetivo, sujeta a un conjunto de desigualdades lineales, denominadas restricciones.
$$\begin{array}{l} F(x,y)=ax+by & \hbox{ (Función objetivo) }\\ \end{array}$$ $$\left\{\begin{array}{l} a_1x+b_1y \leq c_1\\ \vdots\\ a_nx+b_ny \leq c_n \end{array}\right. \hbox{ (Conjunto de restricciones del problema)}$$-
Representar gráficamente cada una de las restricciones, identificando los semiplanos.
-
Determinar la región factible y los vértices de la misma, resolviendo los sistemas de dos ecuaciones con dos incógnitas que determinan cada uno de los vértices.
-
Comprobar si la región factible es convexa y acotada para tener garantía de la existencia de valores máximos y mínimos.
-
Sustituir las coordenadas de los vértices en la función objetivo para obtener el valor máximo y el valor mínimo (según sea el problema)
-
El vértice en el que la función objetivo tome el valor mínimo (máximo), será el mínimo (máximo) del problema de optimización.
Nota: Una región del plano es convexa si dados dos puntos cualesquiera de la misma, el segmento que los une está contenido en dicha región. $$A \subseteq \mathbb{R^2} \hbox{ es convexo} \Leftrightarrow \forall P,Q \in A, \overline{PQ} \subseteq A$$ Una región del plano es acotada si existe un número real \( M>0 \) tal que todo valor de x e y es menor que M en valor absoluto. $$A \subseteq \mathbb{R^2} \hbox{ es acotado} \Leftrightarrow \exists M>0 \hbox{ / } |x| \leq M,|y| \leq M, \forall (x,y) \in A$$
Resolución gráfica de problemas de Programación Lineal
-
Hallar la región factible y las coordenadas de los vértices de la misma.
-
Representar gráficamente la función objetivo \(F(x,y)=0\).
$$ax+by=0 \Leftrightarrow y=-\frac{a}{b}x$$ -
Trazar rectas paralelas a la función objetivo por cada uno de los vértices de la región factible. Dichas rectas son de la forma: $$F(x,y)=k, k \in \mathbb{R}$$
La función objetivo crece según la dirección del vector \(\overrightarrow{v}=(a,b)\). Por tanto:
-
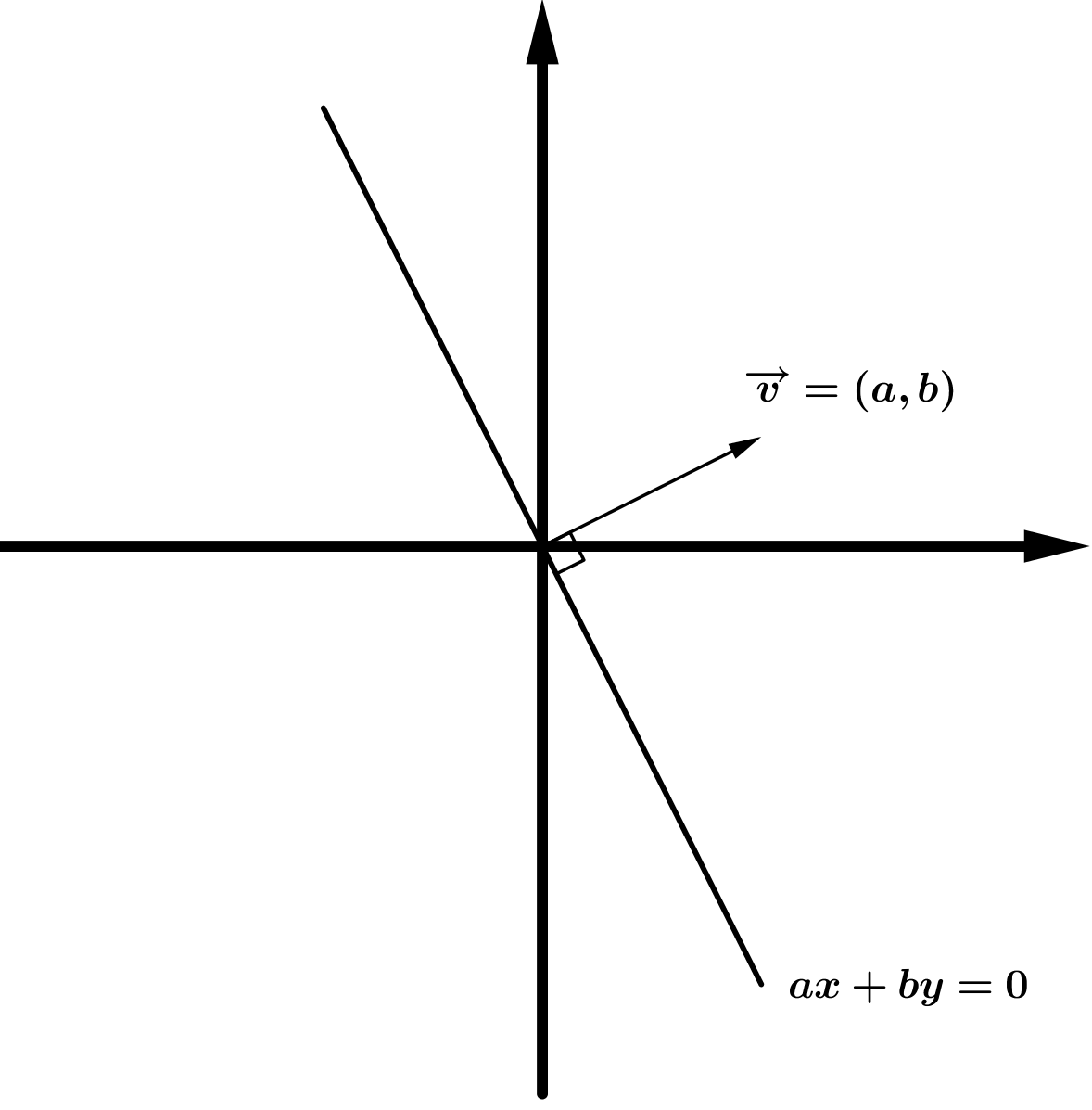
Dada la recta \(ax+by=0\) donde \(a>0 , b>0\) , el máximo (mínimo) se alcanzará en el vértice de la región factible donde la recta paralela a la recta que determina la función objetivo tiene mayor (menor) ordenada en el origen.
-
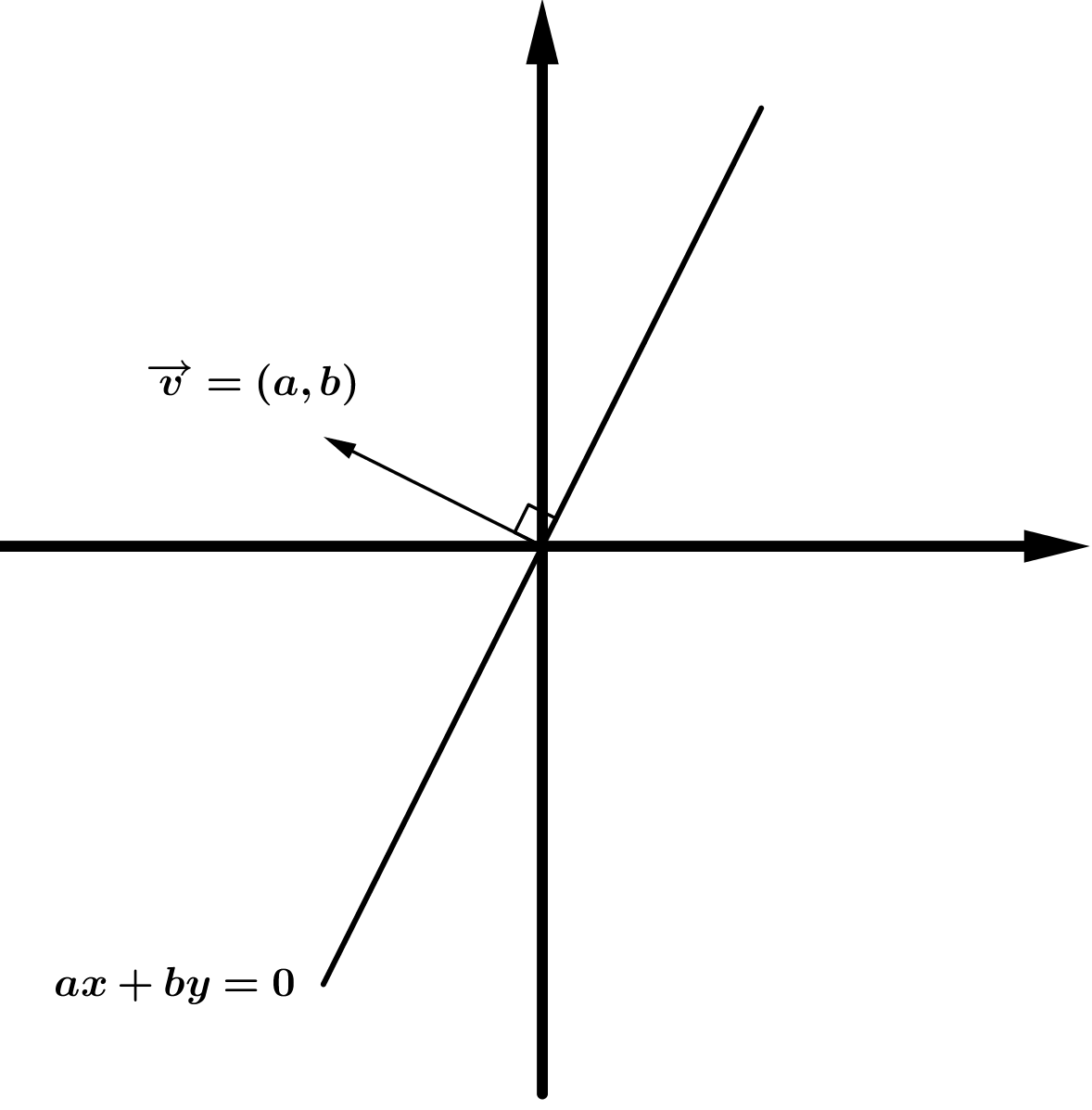
Dada la recta \(ax+by=0\) donde \(a<0 , b>0\) , el máximo (mínimo) se alcanzará en el vértice de la región factible donde la recta paralela a la recta que determina la función objetivo tiene mayor (menor) ordenada en el origen.
-
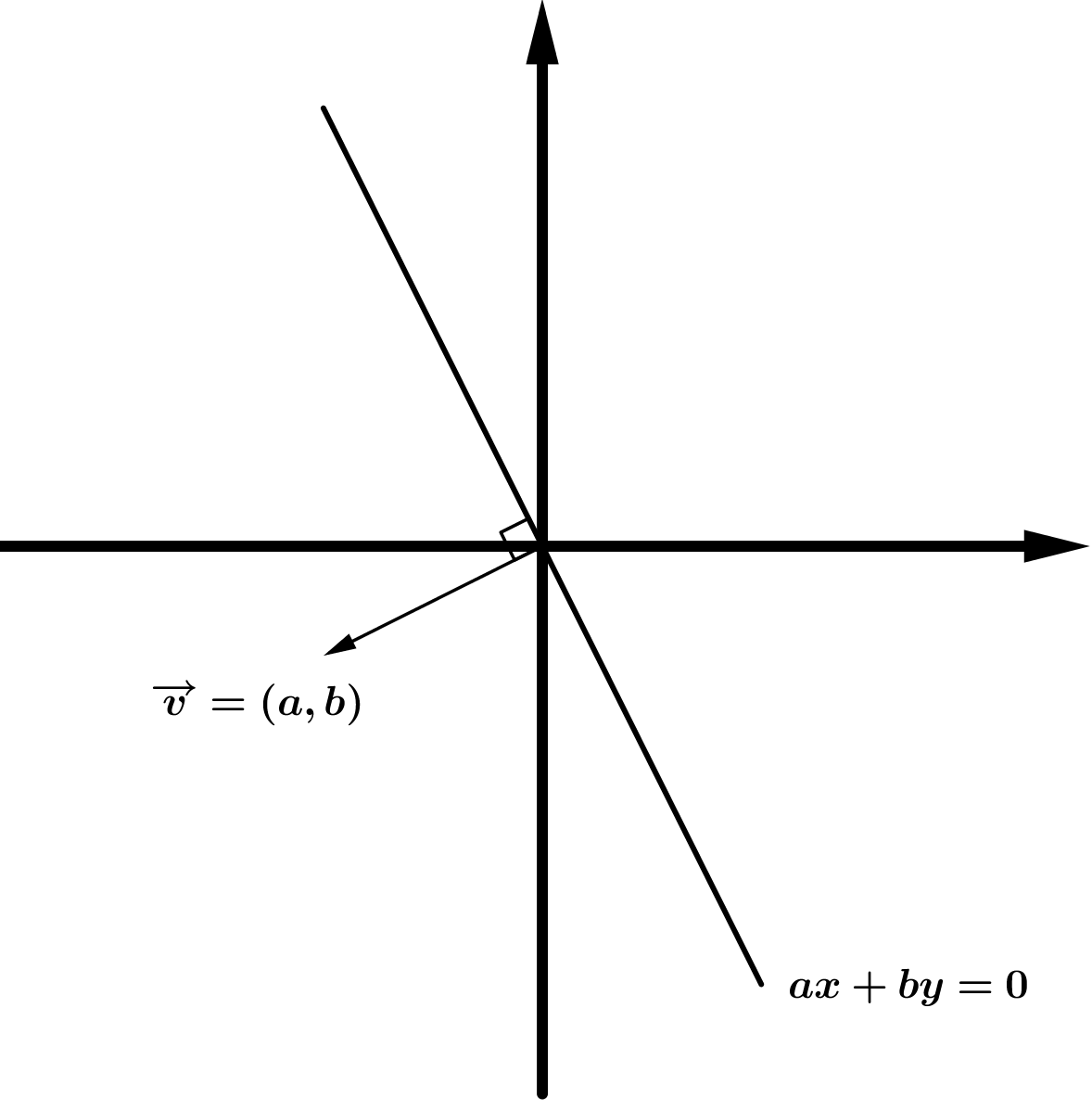
Dada la recta \(ax+by=0\) donde \(a<0 , b<0\) , el máximo (mínimo) se alcanzará en el vértice de la región factible donde la recta paralela a la recta que determina la función objetivo tiene menor (mayor) ordenada en el origen.
-
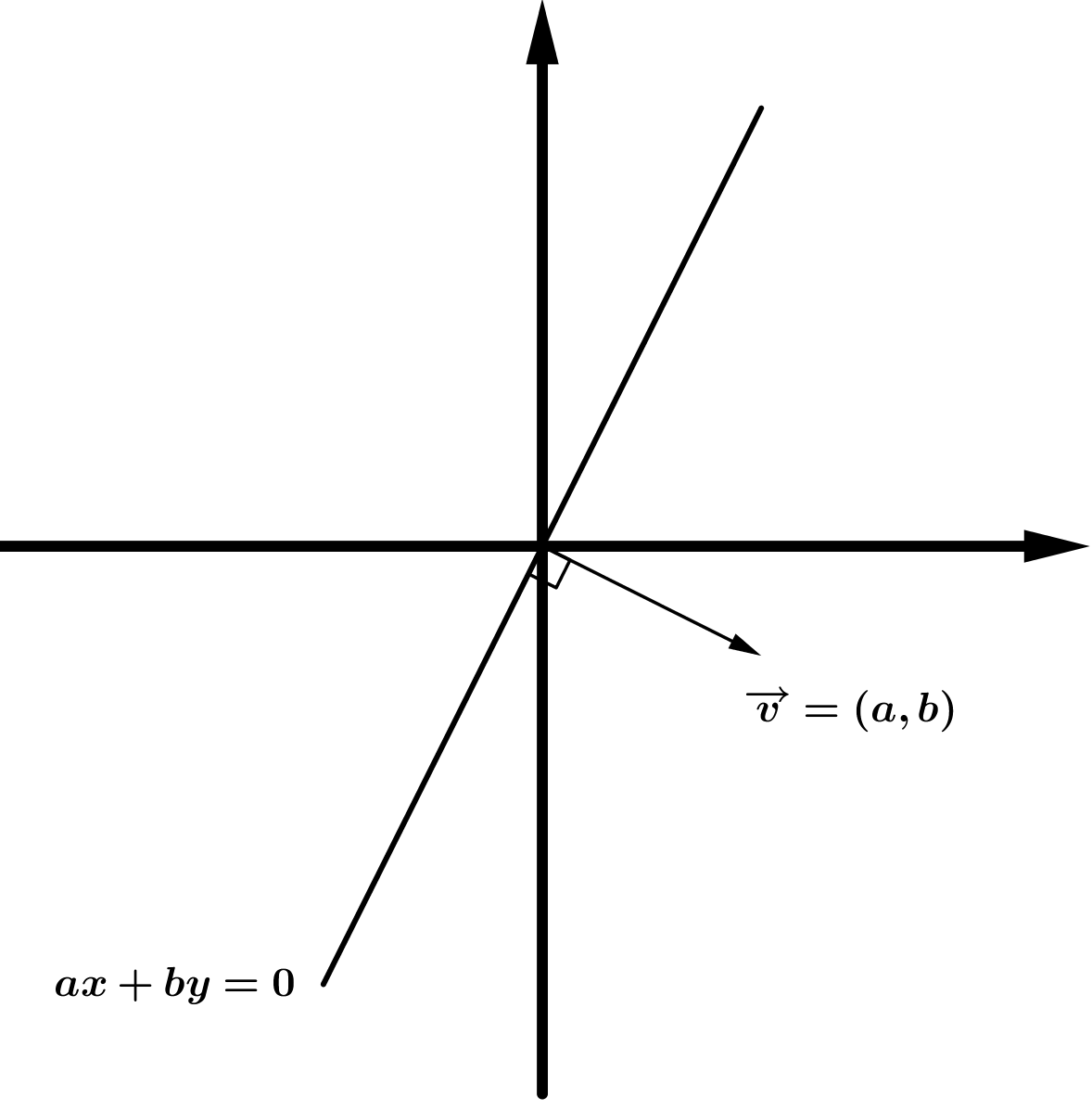
Dada la recta \(ax+by=0\) donde \(a>0 , b<0\) , el máximo (mínimo) se alcanzará en el vértice de la región factible donde la recta paralela a la recta que determina la función objetivo tiene menor (mayor) ordenada en el origen.
| \( a>0, b>0 \) | \( a<0, b>0 \) | |
|
|
|
| \( a<0, b<0 \) | \( a>0, b<0 \) | |
|
|
-
Dada la recta \(ax=0\) donde \(a>0 , b=0\) , el máximo (mínimo) se alcanzará en el vértice de la región factible donde la recta paralela a la recta que determina la función objetivo tiene mayor (menor) abscisa.
-
Dada la recta \(ax=0\) donde \(a<0 , b=0\) , el máximo (mínimo) se alcanzará en el vértice de la región factible donde la recta paralela a la recta que determina la función objetivo tiene menor (mayor) abscisa.
-
Dada la recta \(by=0\) donde \(a=0 , b>0\) , el máximo (mínimo) se alcanzará en el vértice de la región factible donde la recta paralela a la recta que determina la función objetivo tiene mayor (menor) ordenada en el origen.
-
Dada la recta \(by=0\) donde \(a=0 , b<0\) , el máximo (mínimo) se alcanzará en el vértice de la región factible donde la recta paralela a la recta que determina la función objetivo tiene menor (mayor) ordenada en el origen.
Obtención del conjunto de restricciones a partir de la región factible
-
Calcular las ecuaciones de las rectas que pasan por cada dos vértices consecutivos de la región factible.
-
Tomar un punto interior de la región factible y sustituir sus coordenadas en cada una de las ecuaciones de las rectas obtenidas en el paso anterior. Según corresponda, escribiremos la desigualdad que se verifique.
-
Escribir el conjunto de restricciones formado por cada una de las desigualdades anteriores.
Nota: Debes recordar cómo obtener la ecuación de la recta que pasa por dos puntos. Dados los puntos \(A=(x_1,y_1)\) y \(B =(x_2,y_2)\), la pendiente de la recta que pasa por los puntos \(A\) y \(B\) es: $$m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$$ La ecuación punto-pendiente de la recta que pasa por los puntos \(A\) y \(B\) es: $$\begin{array}{l} y-y_1=m(x-x_1) & ó & y-y_2=m(x-x_2)\\ \end{array}$$ También puedes obtener la ecuación de la recta \(y=mx+n\) sustituyendo las coordenadas de los puntos \(A=(x_1,y_1)\) y \(B=(x_2,y_2)\) en la ecuación de la recta y resolver un sistema de 2 ecuaciones con 2 incógnitas para obtener los valores de m y n: $$\left\{\begin{array}{l} y_1=mx_1+n\\ y_2=mx_2+n \end{array}\right.$$

