PROBABILIDAD (FORMULARIOS)

Probabilidad

Sucesos y operaciones con sucesos

$$\left\{\begin{array}{l} \mathbf{\hbox{Suceso seguro }} X \\ \mathbf{\hbox{Suceso imposible }} \varnothing \end{array}\right.$$ $$\mathbf{\hbox{Intersección de sucesos}}$$ $$A \cap B = \begin{Bmatrix} x / x \in A \wedge x \in B \end{Bmatrix}$$ $$\mathbf{\hbox{Unión de sucesos}}$$ $$A \cup B = \begin{Bmatrix} x / x \in A \vee x \in B \end{Bmatrix}$$ $$\mathbf{\hbox{Diferencia de sucesos}}$$ $$A - B =\begin{Bmatrix} x / x \in A \wedge x \notin B \end{Bmatrix} = A \cap \overline{B}$$ $$\mathbf{\hbox{Contrario o complementario de un suceso}}$$ $$\overline{A} = \begin{Bmatrix} x / x \notin A \end{Bmatrix}$$ $$\overline{A} = X - A$$ $$\overline{\overline{A}} = A$$ $$X = A \cup \overline{A}$$ $$A= (A \cap B) \cup (A \cap \overline{B})$$ $$\mathbf{\hbox{Leyes de Morgan}}$$ $$\left\{\begin{array}{l} \overline{A \cup B} = \overline{A} \cap \overline{B}\\ \overline{A \cap B} = \overline{A} \cup \overline{B}\\ \end{array}\right.$$ $$\mathbf{\hbox{Incompatibilidad de sucesos}}$$ $$\hbox{A y B son incompatibles} \Leftrightarrow A \cap B = \varnothing$$

Cálculo de Probabilidades

$$P(\varnothing)=0, P(X)=1$$ $$\varnothing \subseteq A \subseteq X \Rightarrow 0 \leq P(A) \leq 1$$ $$\mathbf{\hbox{Probabilidad de la unión}}$$ $$\left\{\begin{array}{l} P(A \cup B) = P(A) + P(B) - P(A \cap B) \\ \\ \hbox{Si A y B incompatibles} \Rightarrow P(A \cup B) = P(A) + P(B) \\ \end{array}\right.$$

En general, dados \(n\) sucesos \(A_1\), \(A_2\), \(\cdots\), \(A_n\):

$$P(A_1 \cup \cdots \cup A_n) = \sum_{i=1}^{n}P(A_i) - \sum_{i \neq j}^{}P(A_i \cap A_j) + \sum_{i \neq j \neq k}^{}P(A_i \cap A_j \cap A_k) - \cdots +(-1)^n P(A_1 \cap \cdots \cap A_n)$$ $$\hbox{Si } \forall i \neq j, A_i \hbox{ y } A_j \hbox{ son incompatibles} \Rightarrow P(A_1 \cup \cdots \cup A_n) = \sum_{k=1}^{n}P(A_k)\\$$ $$\mathbf{\hbox{Probabilidad del contrario}}$$ $$P(\overline{A})=1-P(A)$$ $$\mathbf{\hbox{Regla de Laplace}}$$

Si todos los sucesos elementales son equiprobables,

$$P(A)=\frac{\hbox{Casos favorables a A}}{\hbox{Casos posibles}}$$

Experiencias compuestas

$$\mathbf{\hbox{Probabilidad condicionada}}$$

La probabilidad de que ocurra \(A\) sabiendo que ha ocurrido \(B\) es:

$$P(A|B)=\displaystyle{\frac{P(A \cap B)}{P(B)}}$$ $$\mathbf{\hbox{Intersección de sucesos}}$$ $$P(A \cap B)=P(A) \cdot P(B|A)$$ $$P(A \cap B \cap C)=P(A) \cdot P(B|A) \cdot P(C|A \cap B)$$ $$P(A_1 \cap \cdots \cap A_n)=P(A_1) \cdot P(A_2|A_1) \cdots P(A_n|A_1 \cap \cdots \cap A_{n-1})$$ $$\mathbf{\hbox{Independencia de sucesos}}$$

\(A\) y \(B\) son independientes si y sólo si:

$$P(A \cap B)=P(A) \cdot P(B) \Leftrightarrow P(A|B)=P(A) \hbox{ si P(B)} \neq 0$$

Sistema completo de sucesos

Un sistema completo de sucesos \(S_{1}, S_{2}, \cdots, S_{n}\) es un conjunto de sucesos cuya unión es el total, es decir, es el espacio muestral \(X\), e incompatibles dos a dos, es decir, la intersección de cualesquiera dos de ellos es el conjunto vacío.

$$ \left\{\begin{array}{l} S_1 \cup \cdots \cup S_n = X\\ S_i \cap S_j=\varnothing \hbox{ } \forall i,j \end{array}\right.$$

Ejemplo:

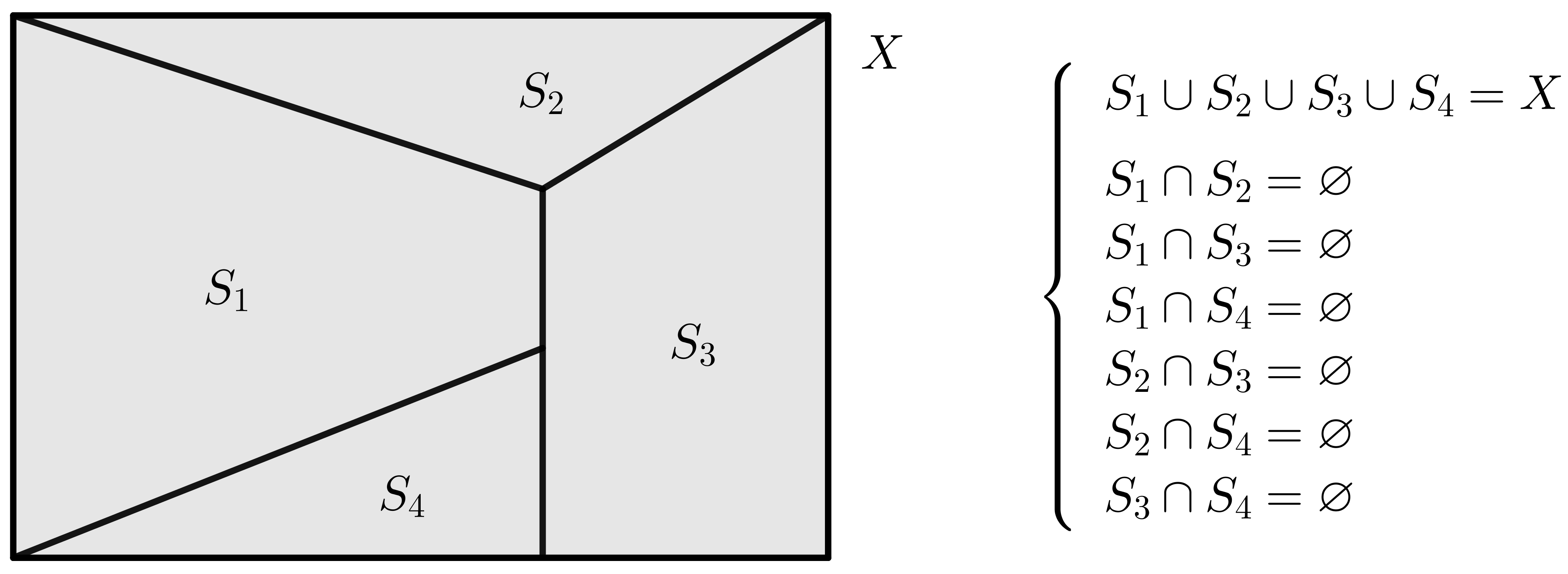
Dado un suceso \(A\), en todo sistema completo de sucesos se cumple:

$$\mathbf{\hbox{Teorema de la Probabilidad Total}}$$ $$P(A)=\displaystyle{\sum_{k=1}^{n}P(S_k)\cdot P(A|S_k)}$$ $$\mathbf{\hbox{Teorema de Bayes}}$$ $$P(S_i|A)=\displaystyle{\frac{P(S_i) \cdot P(A|S_i)}{\displaystyle{\sum_{k=1}^{n}P(S_k)\cdot P(A|S_k)}}}$$

Ejemplo:

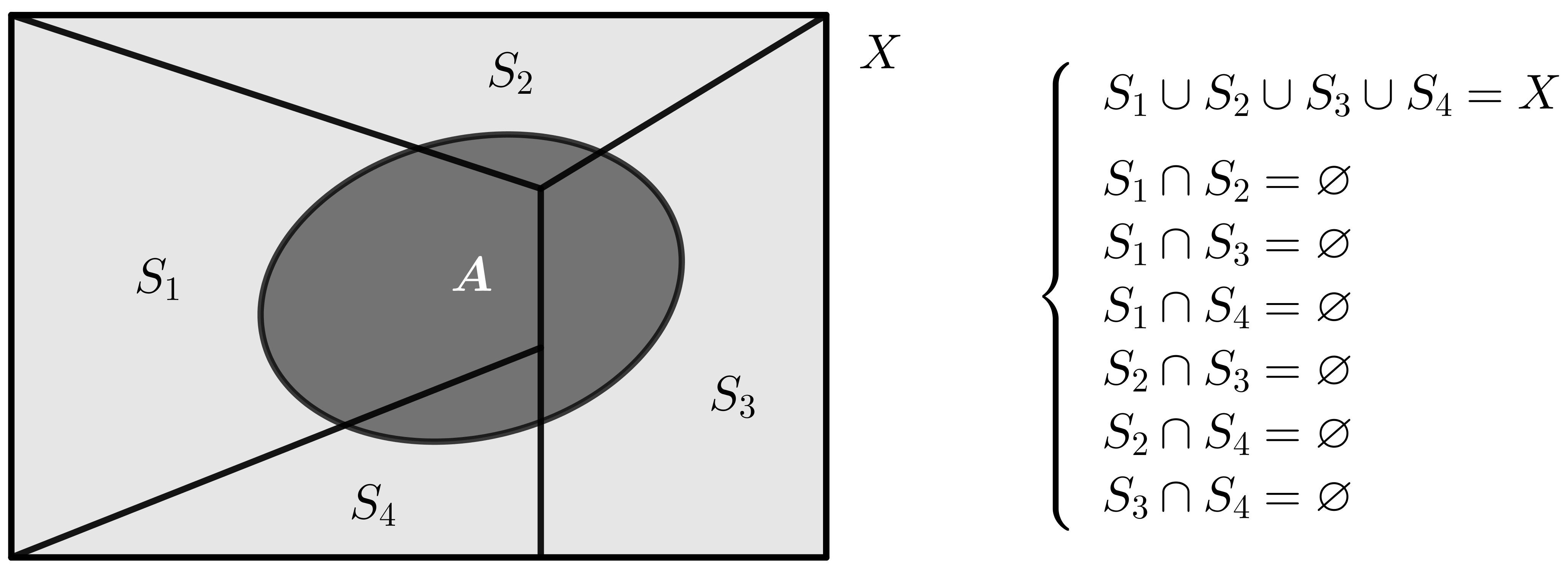
Teorema de la Probabilidad Total:

Teorema de Bayes:

Diagramas de árbol

Ejemplos:

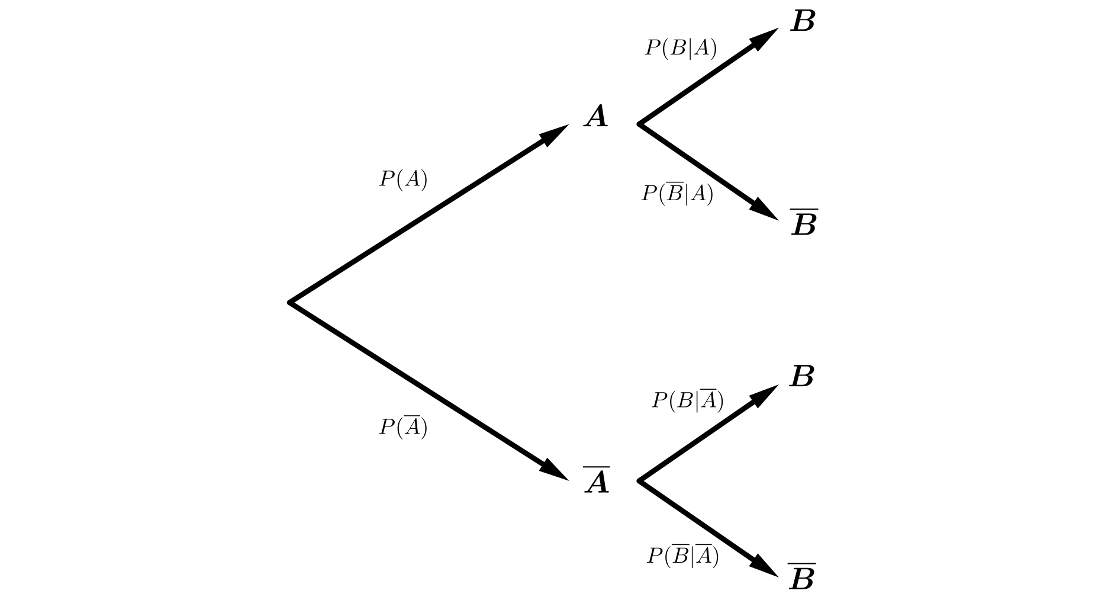
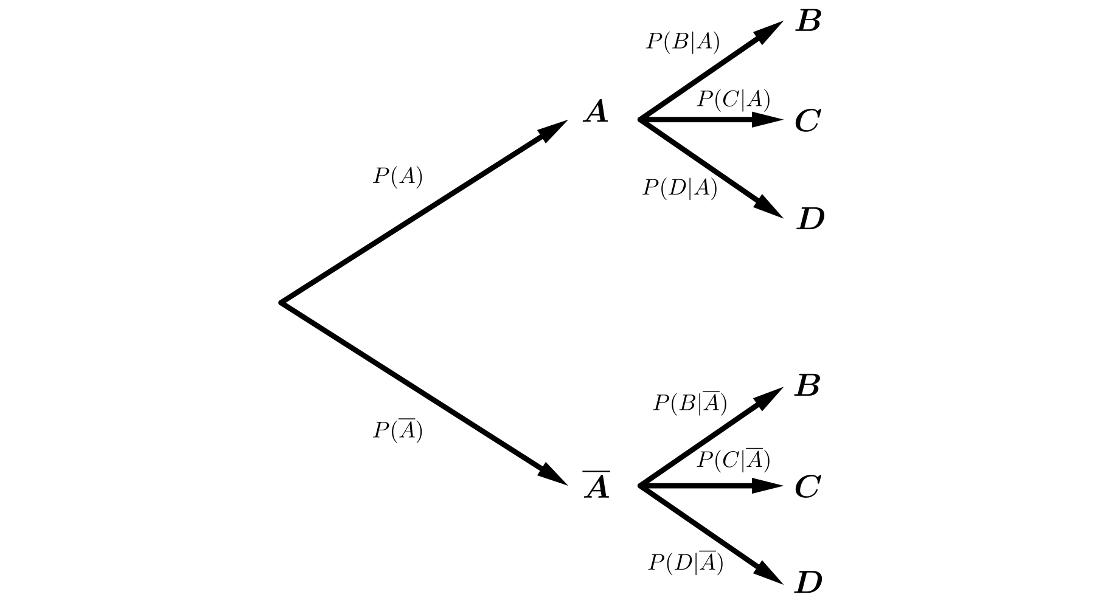
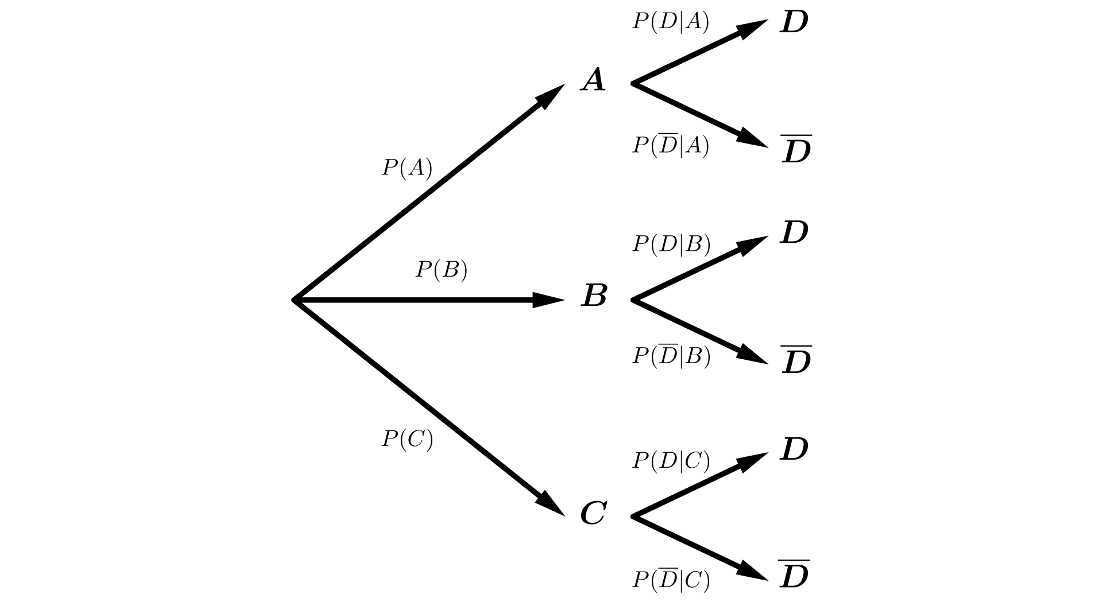
Tablas de contingencia

Ejemplo:

Diagramas de Venn

Dados dos conjuntos A y B:

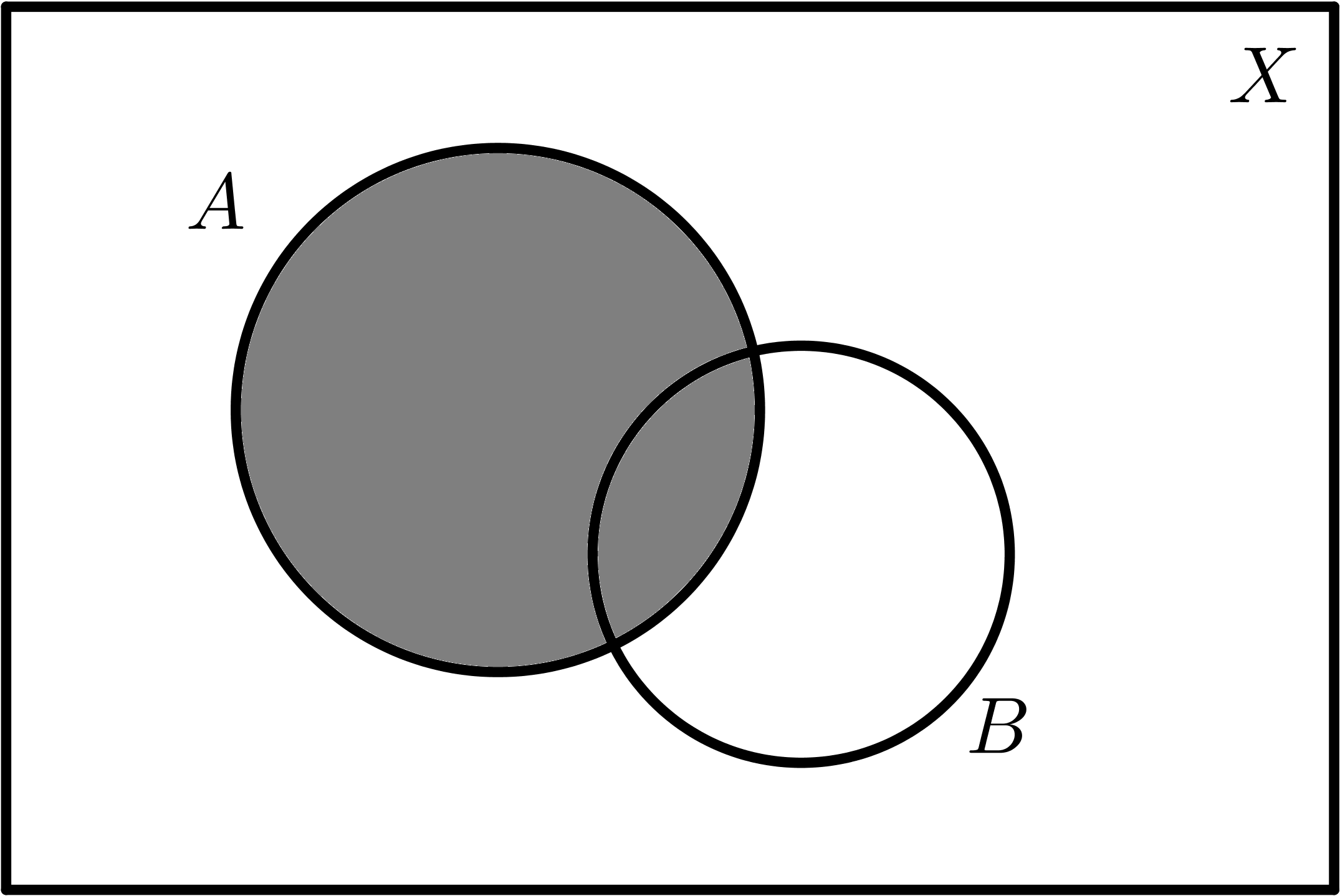
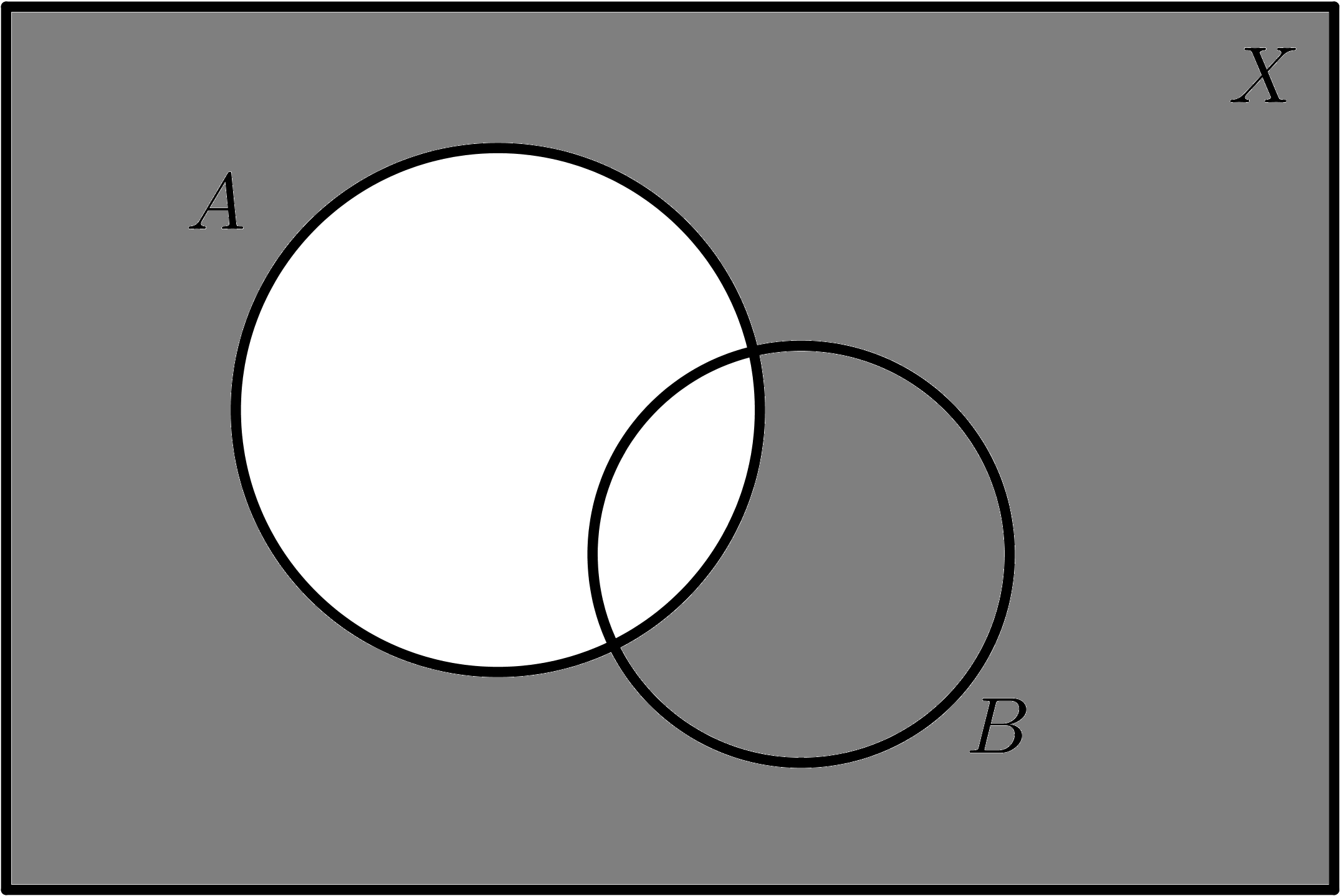
$$A$$	$$\overline{A}$$
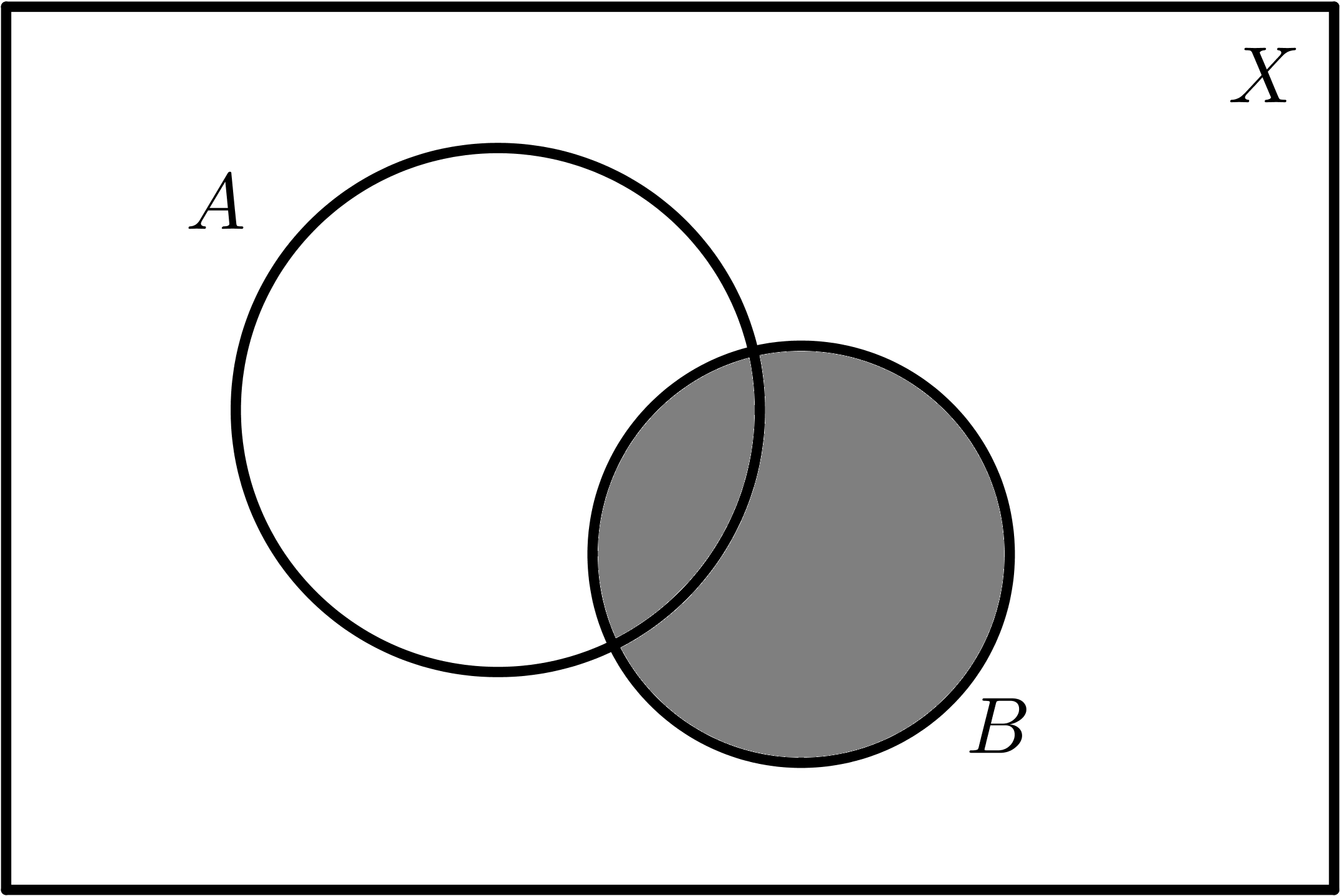
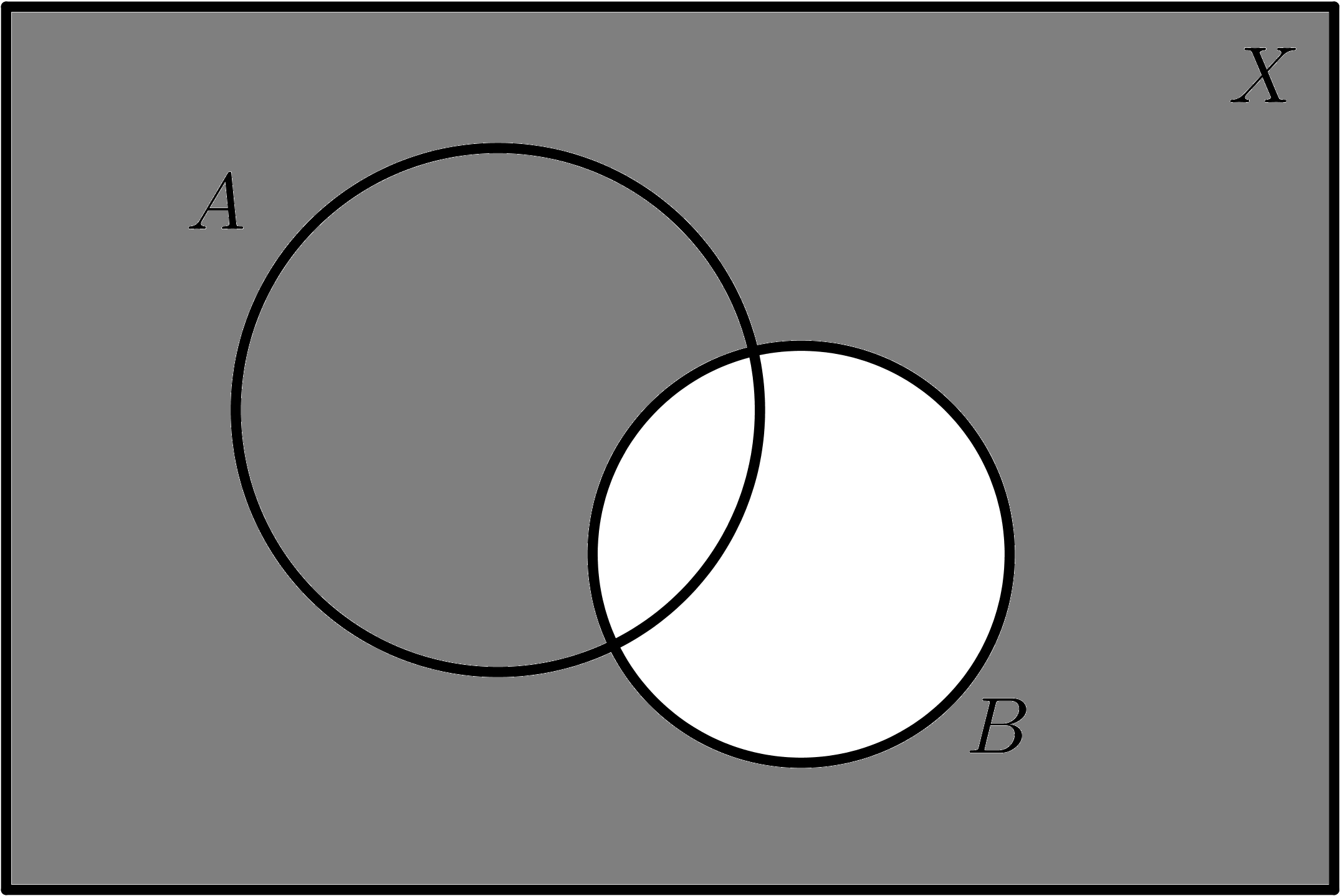
$$B$$	$$\overline{B}$$
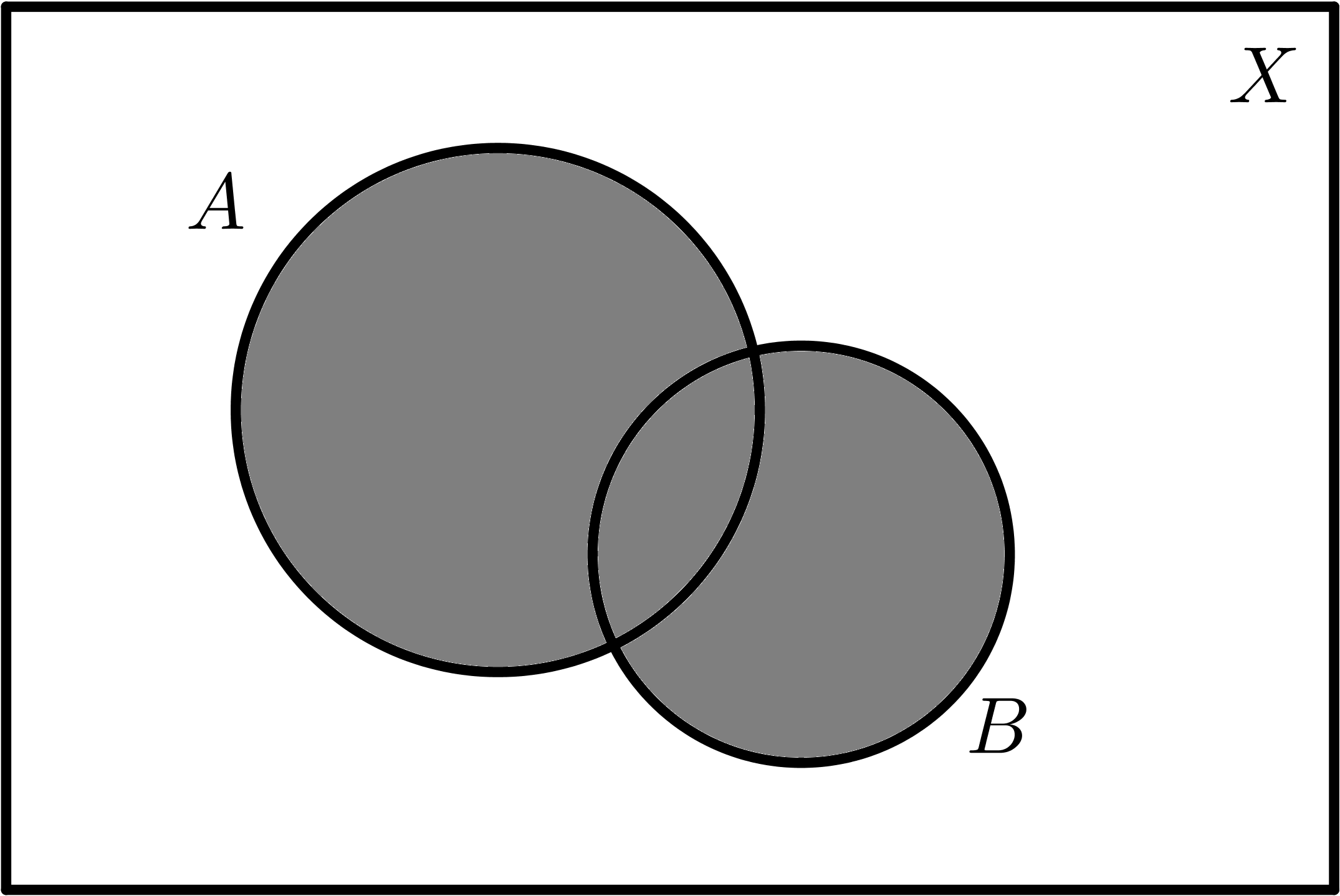
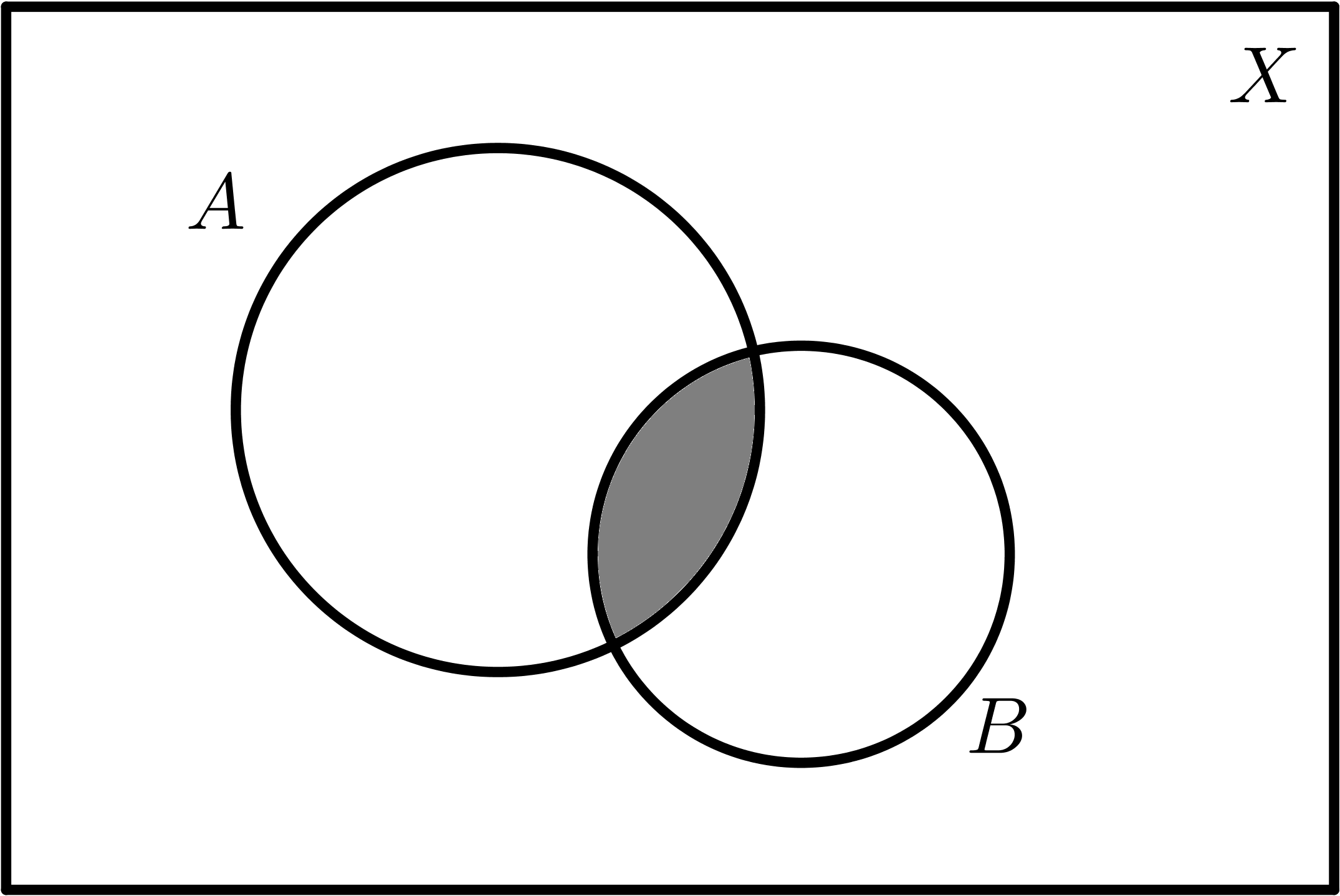
$$A \cup B$$	$$A \cap B$$
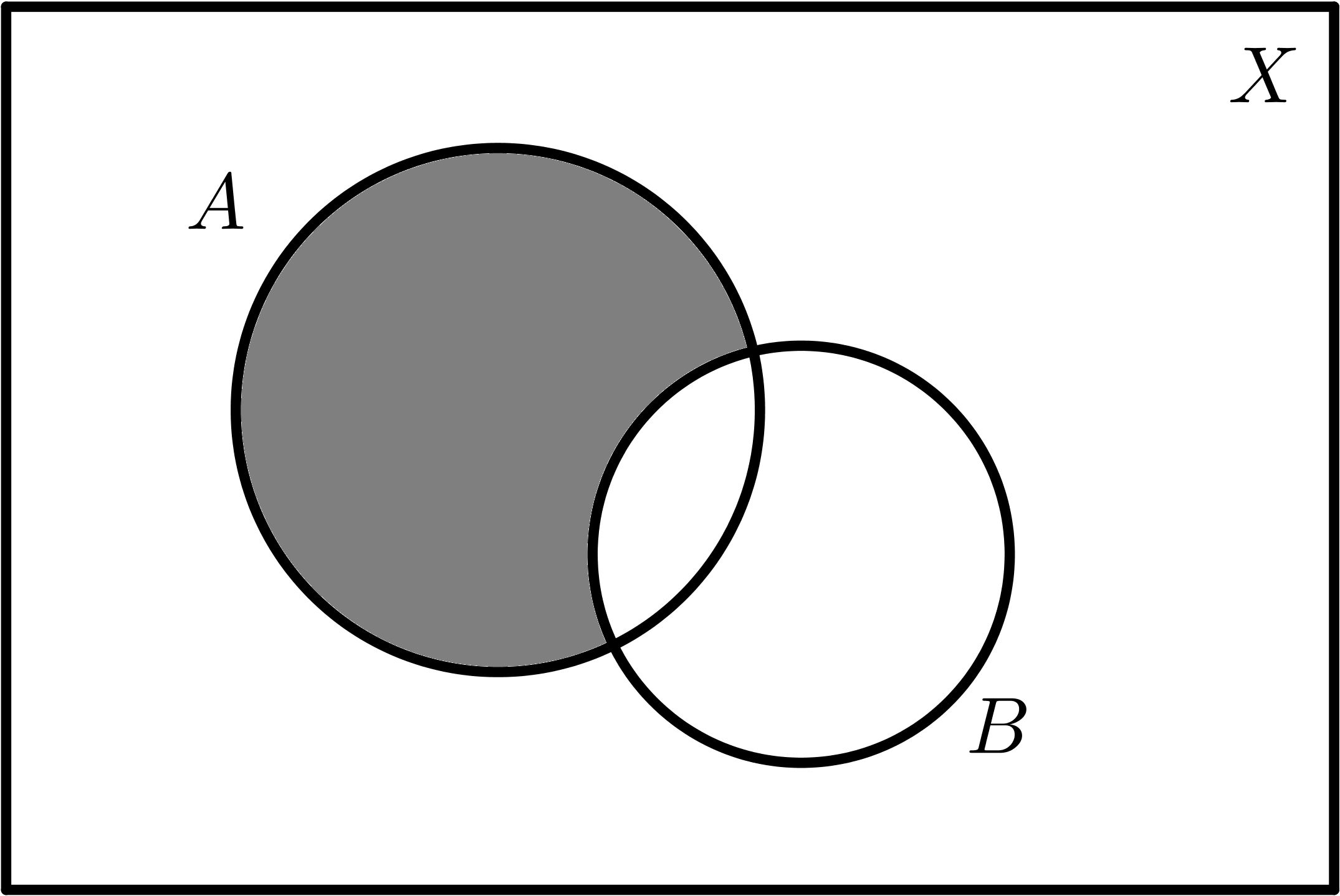
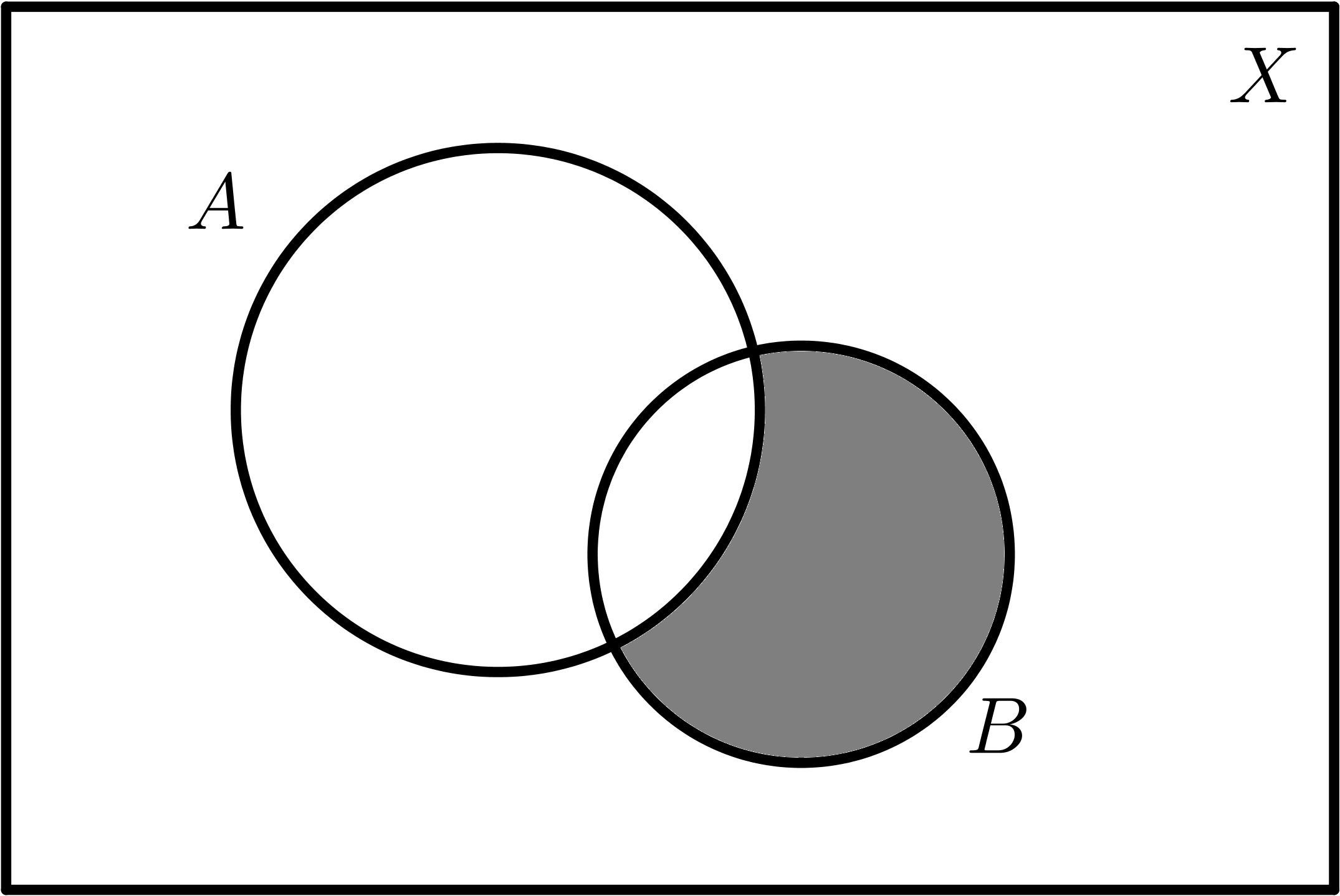
$$A - B$$	$$B - A$$

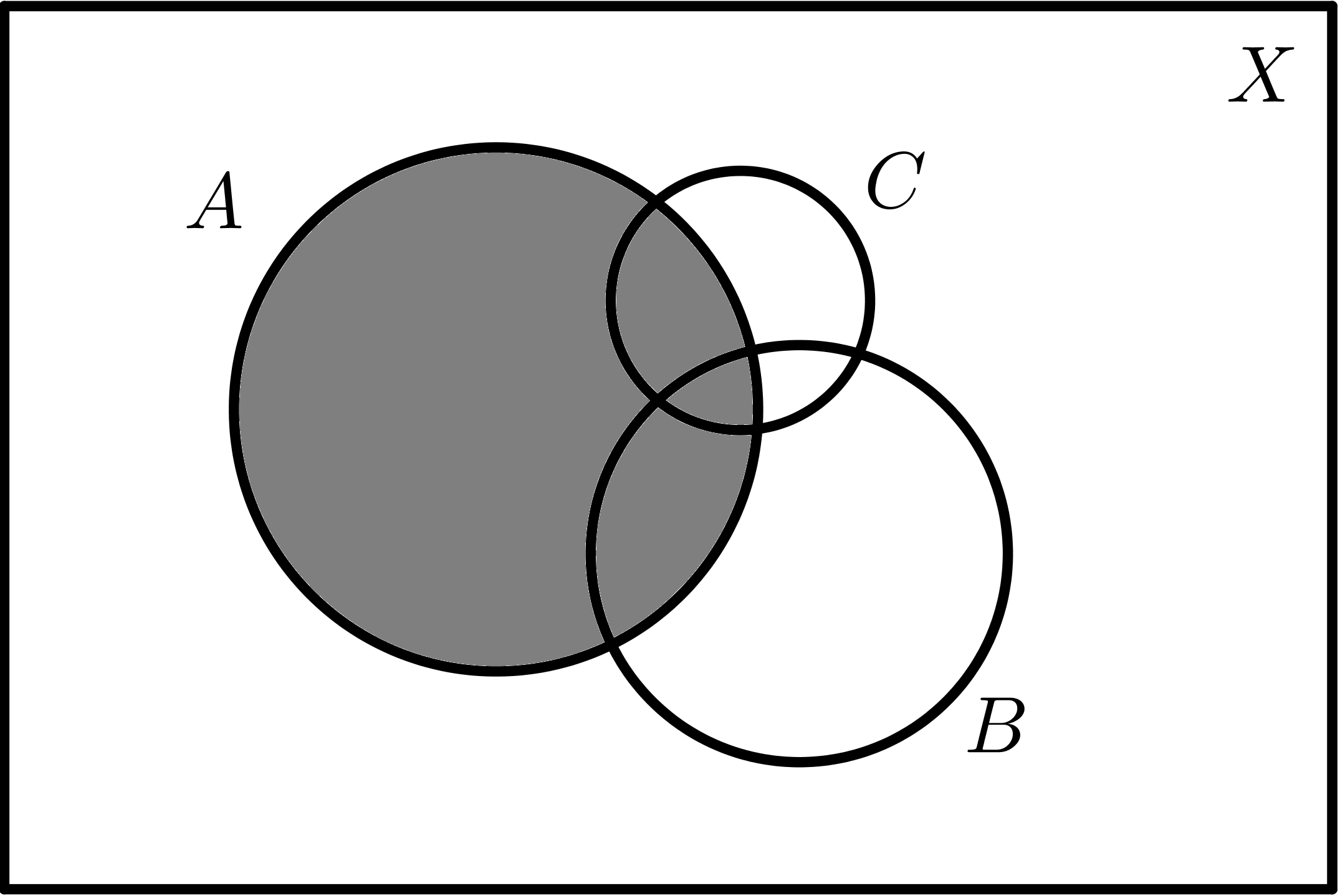
Dados tres conjuntos A, B y C:

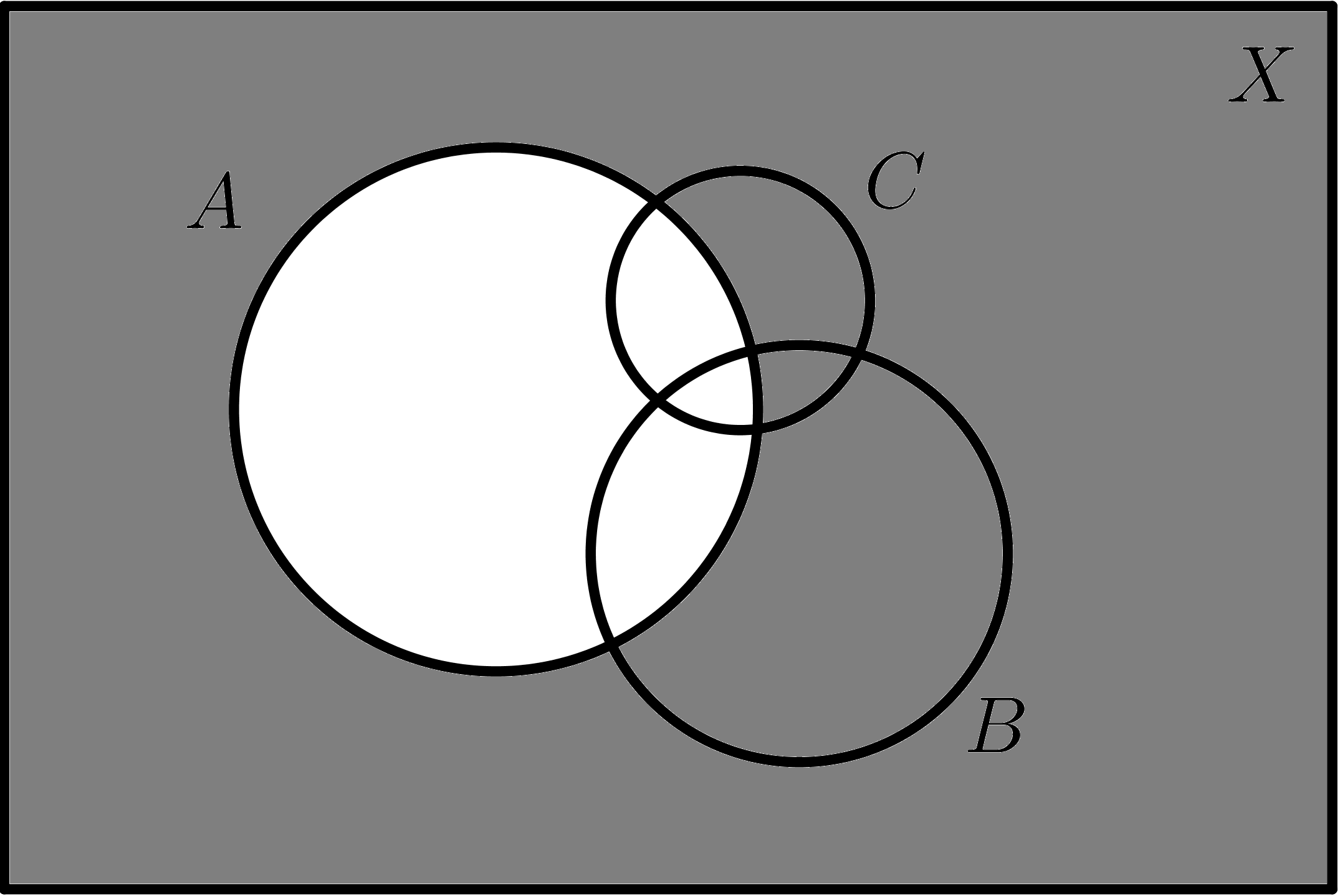
$$A$$	$$\overline{A}$$
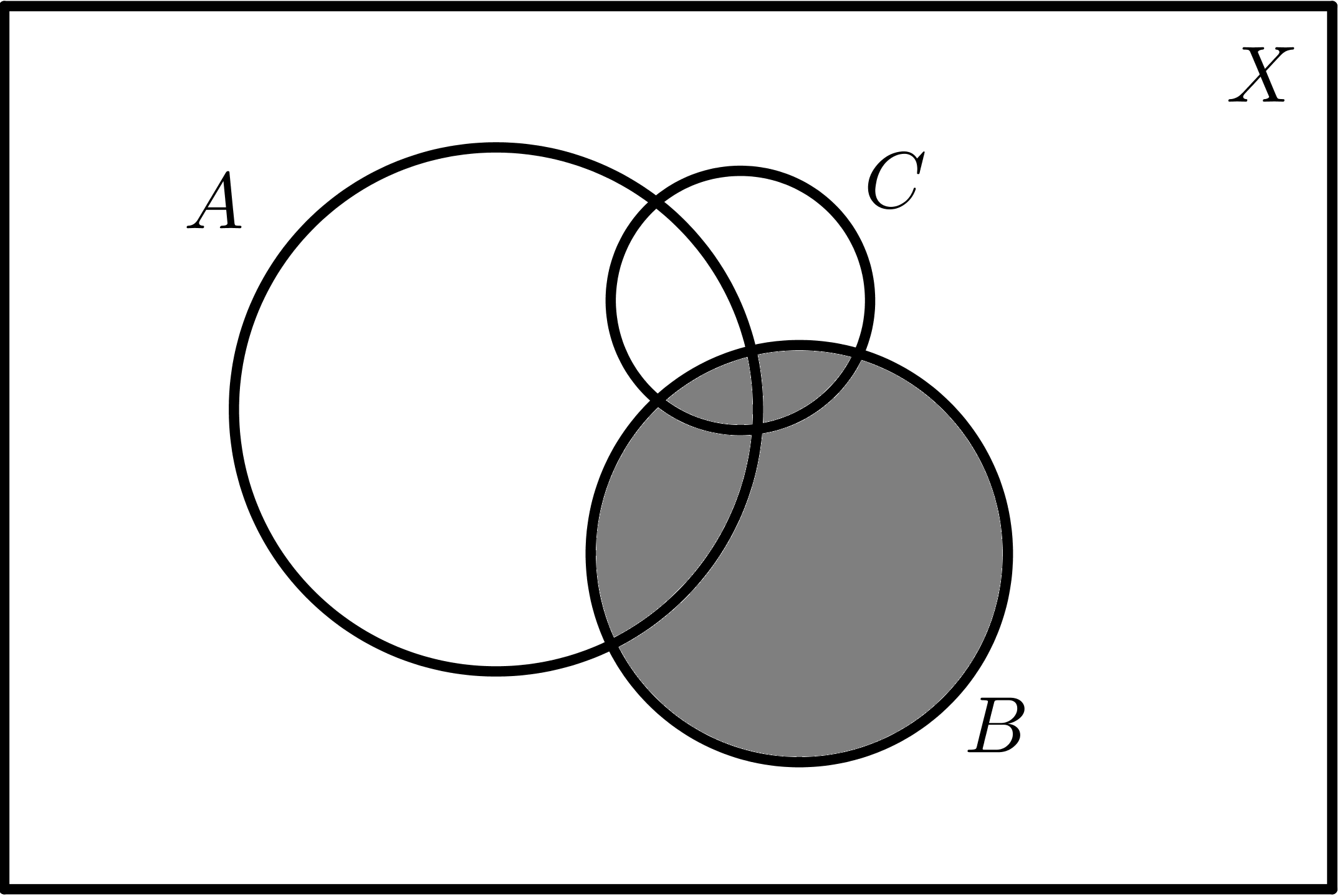
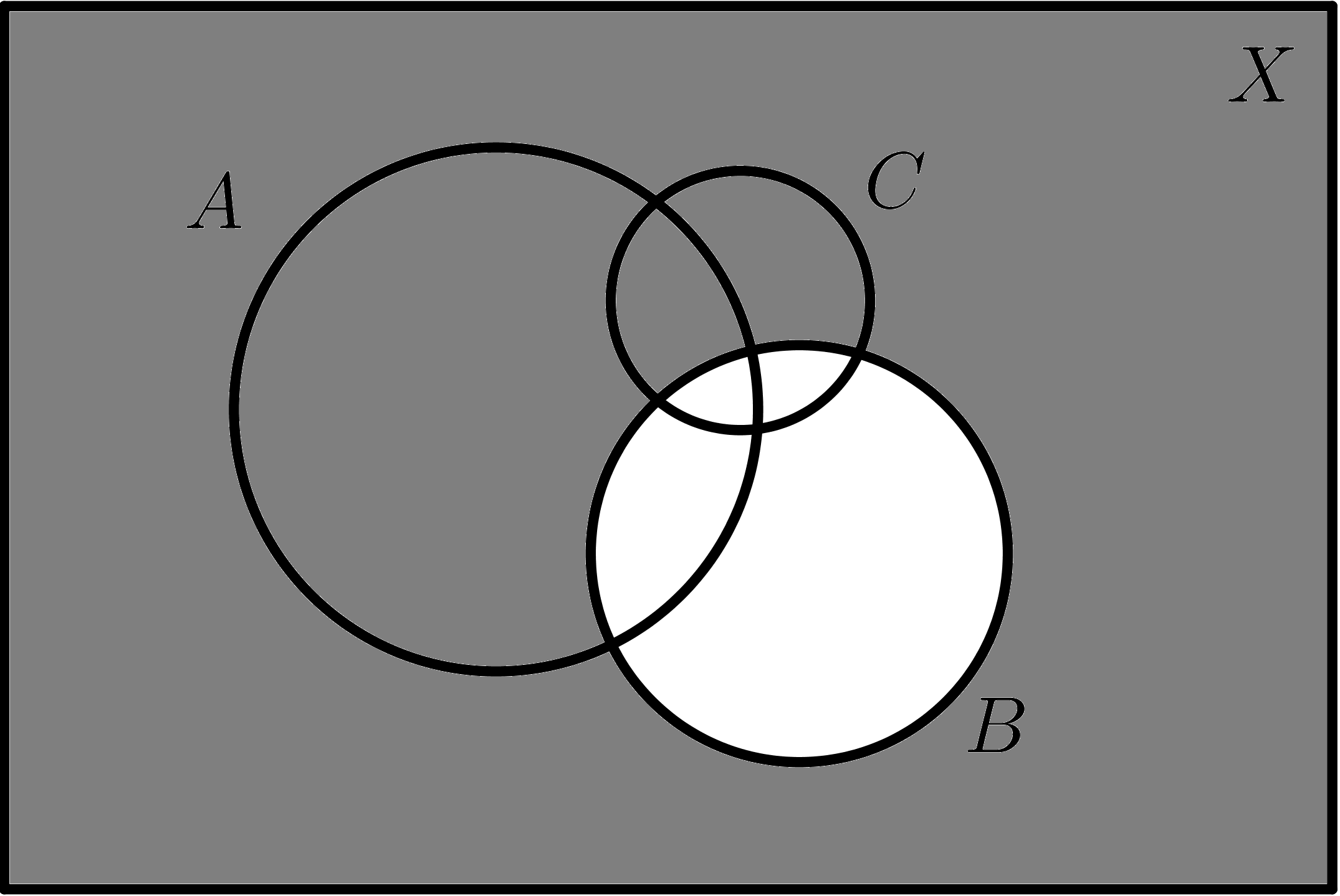
$$B$$	$$\overline{B}$$
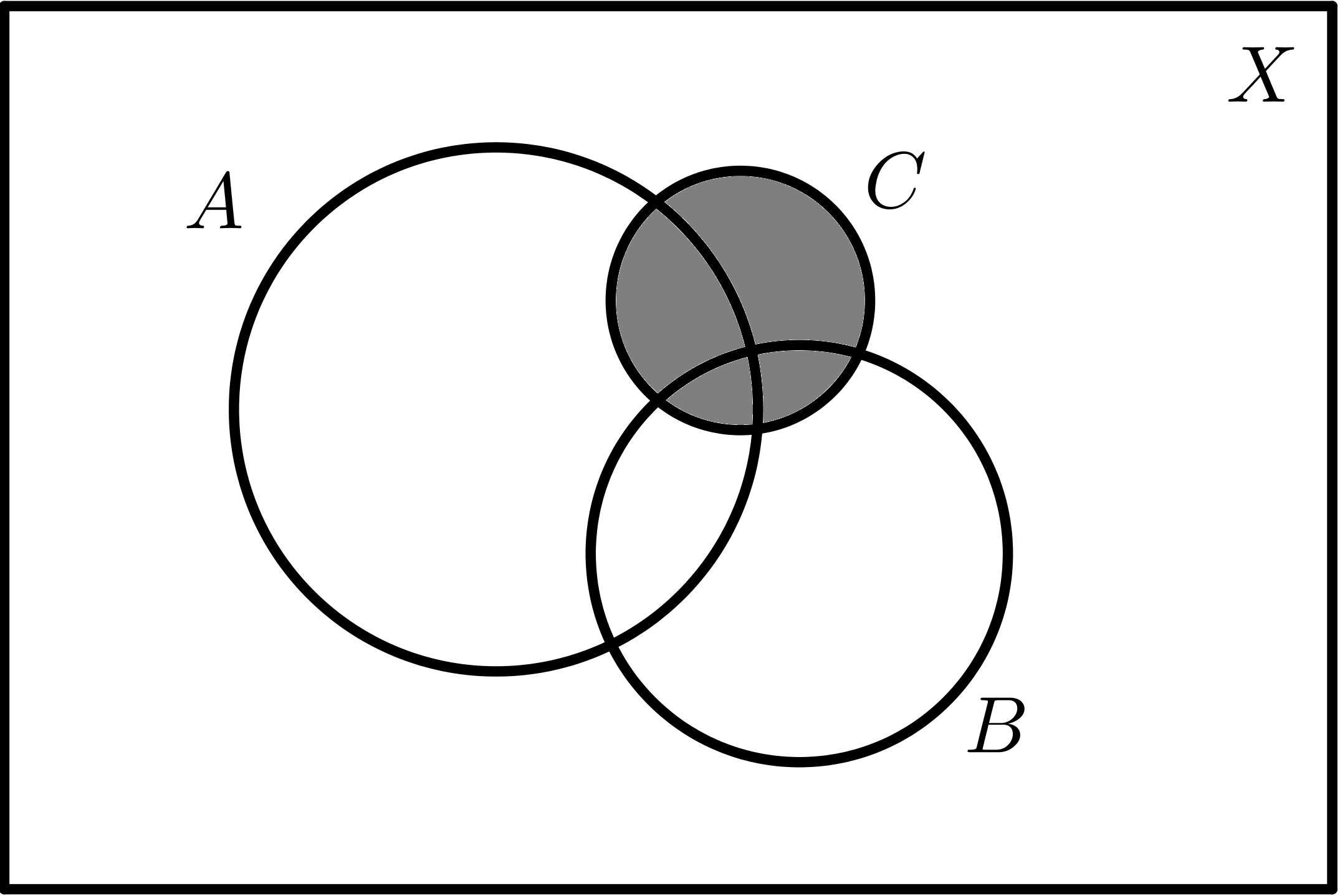
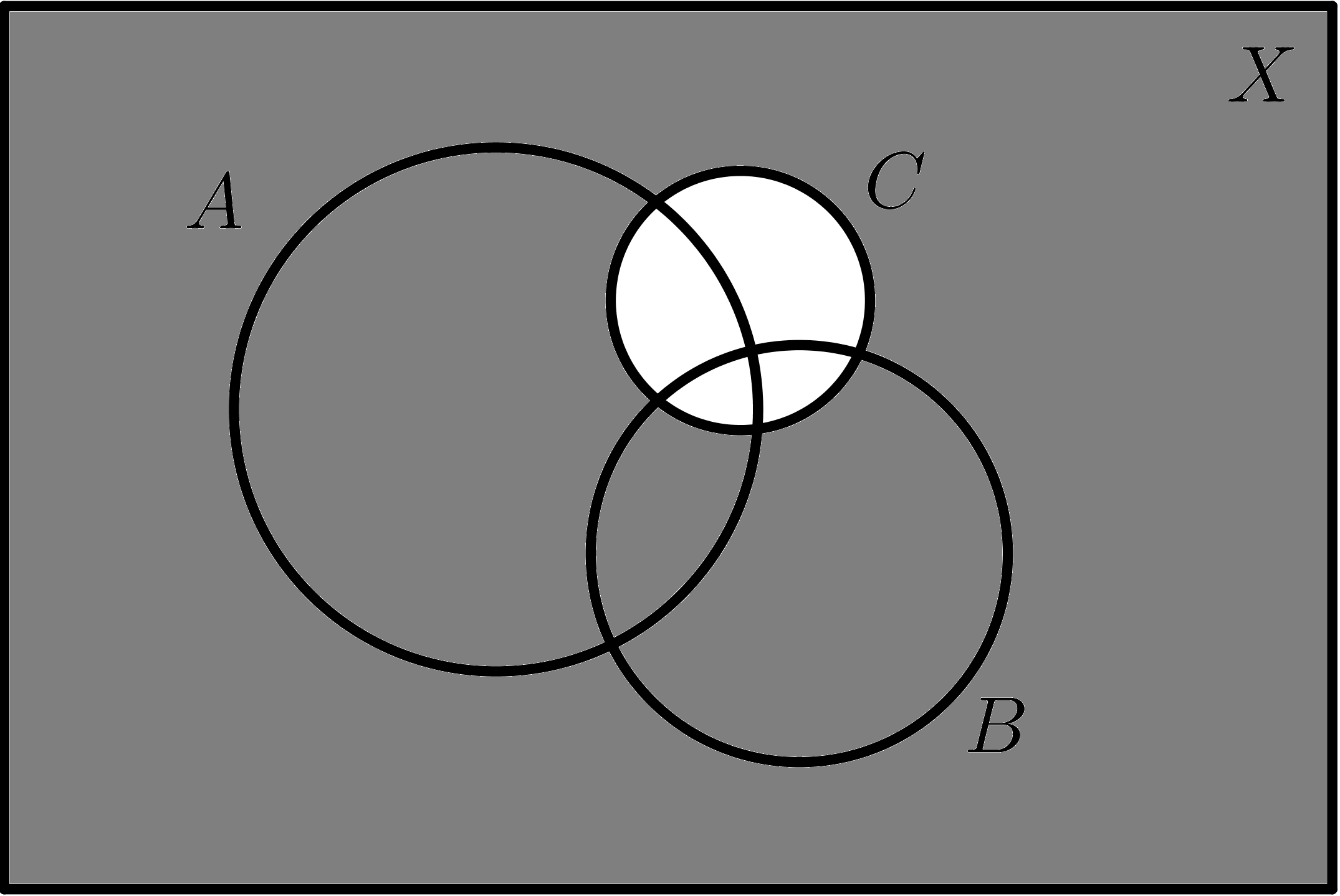
$$C$$	$$\overline{C}$$
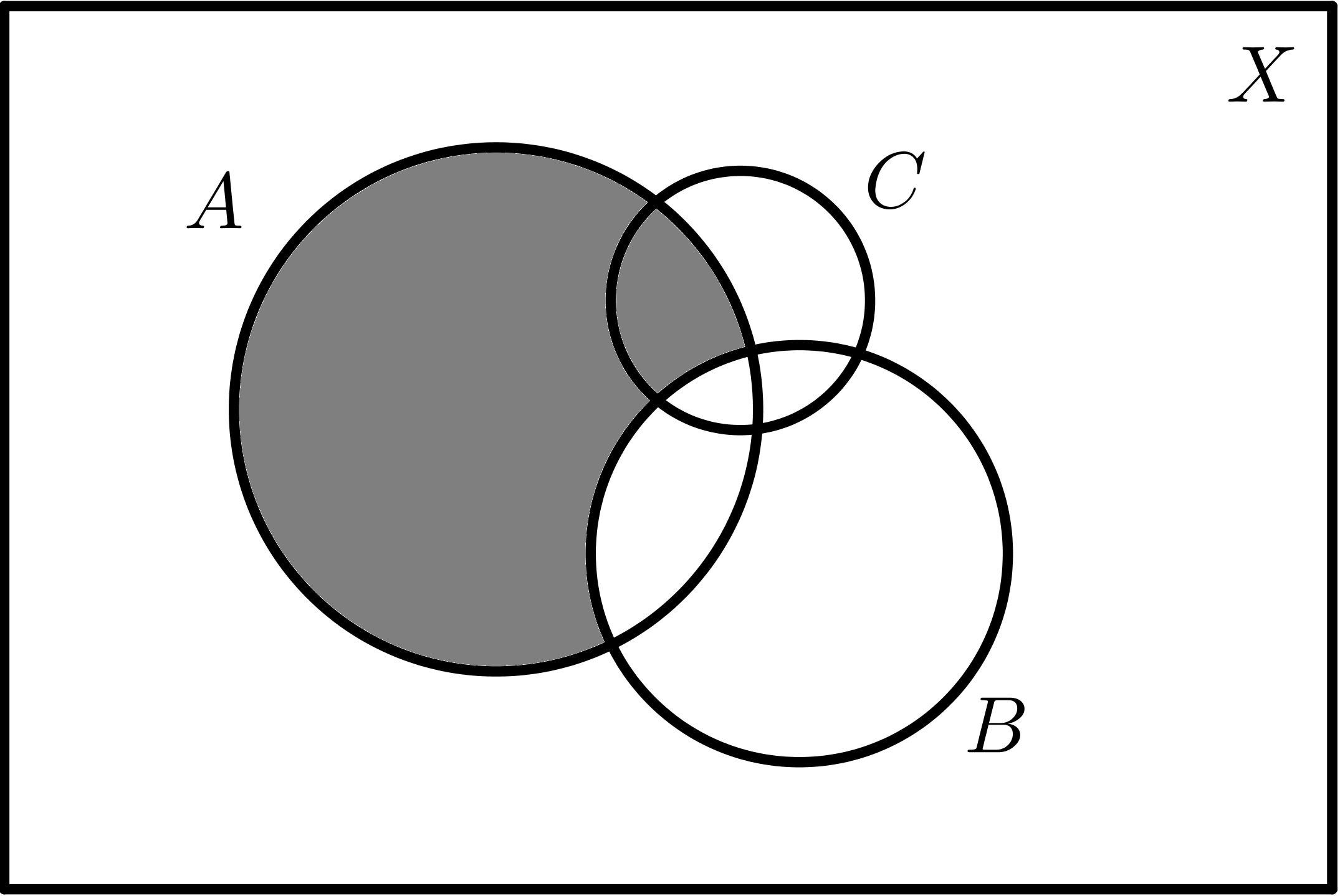
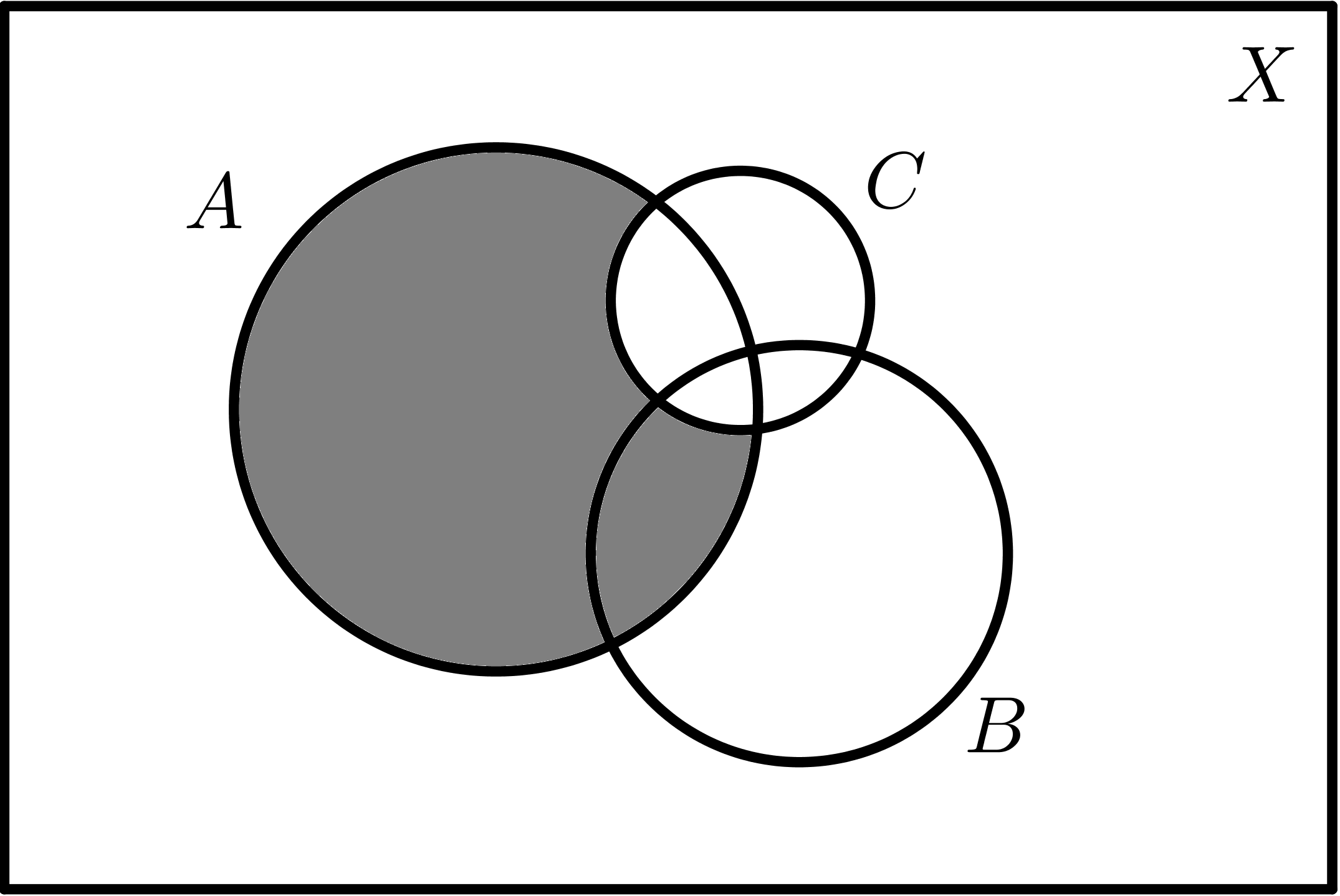
$$A - B$$	$$A - C$$
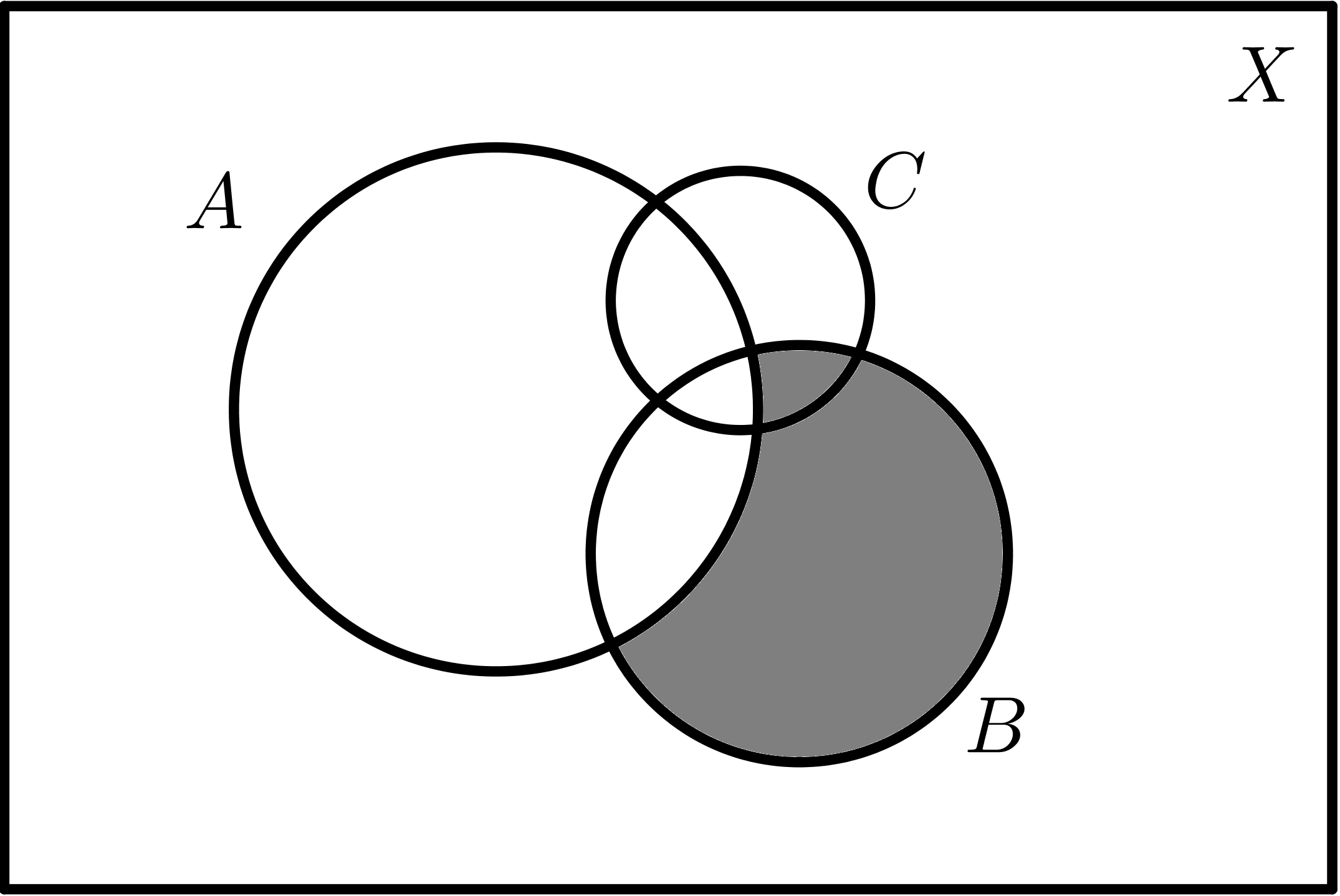
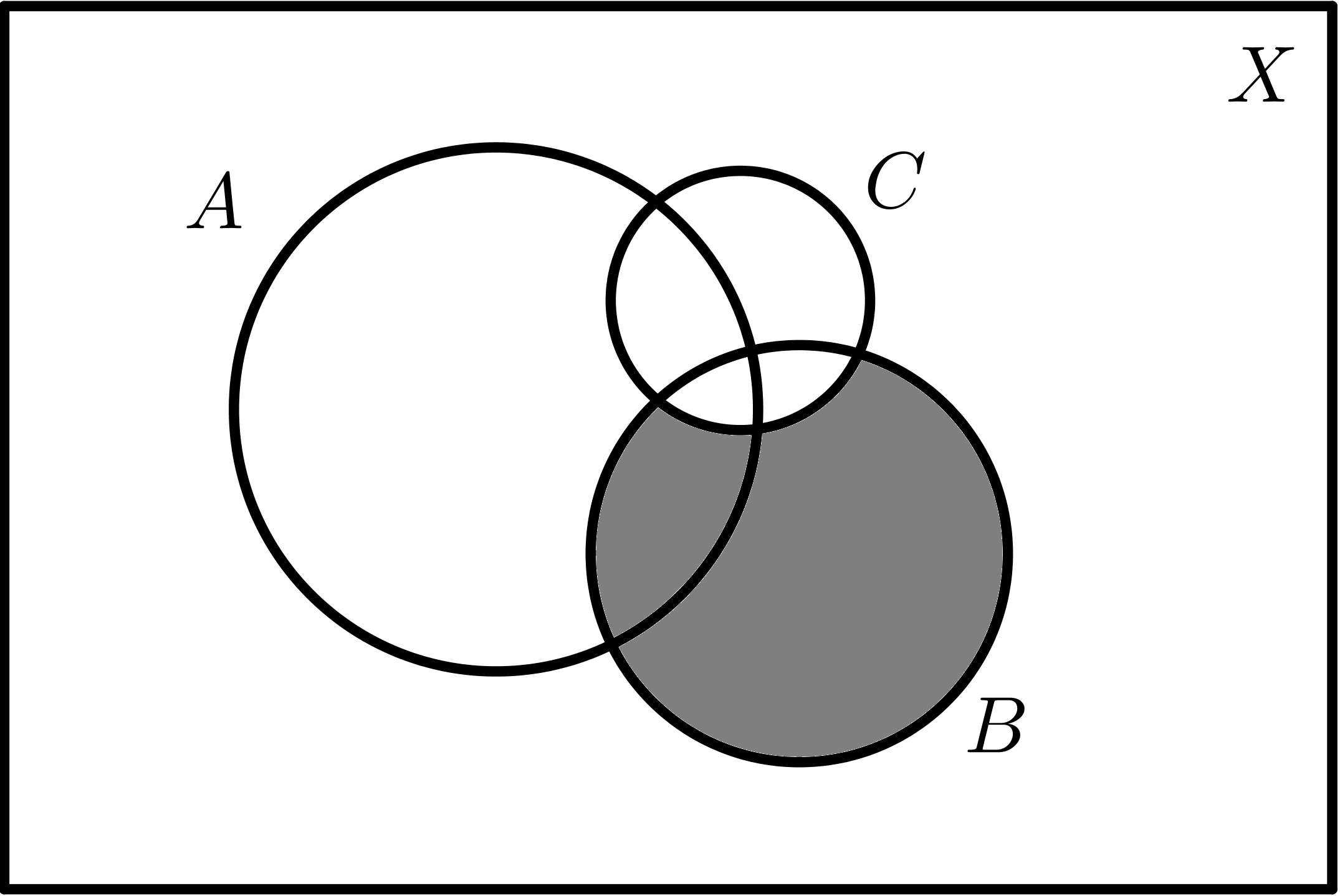
$$B - A$$	$$B - C$$
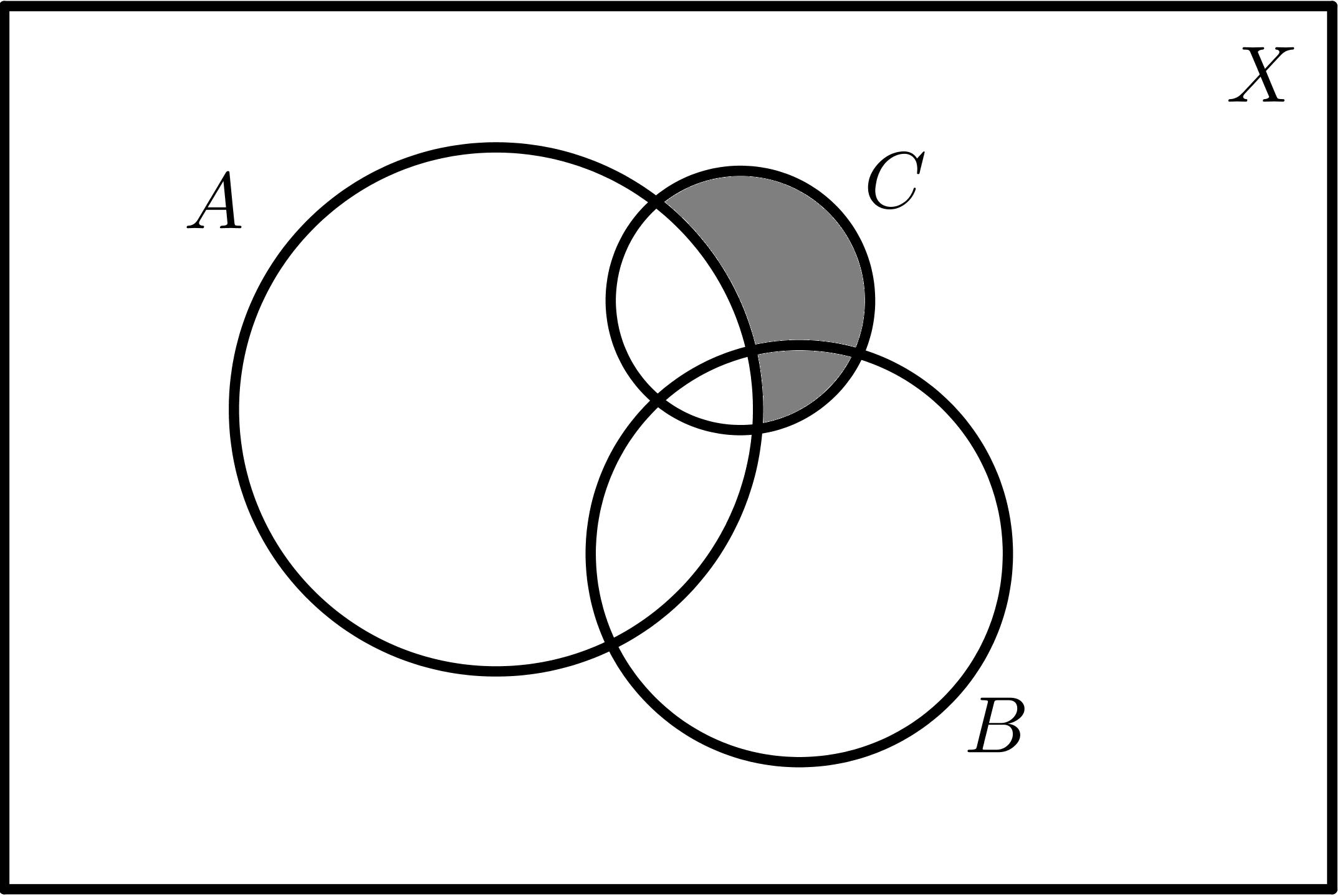
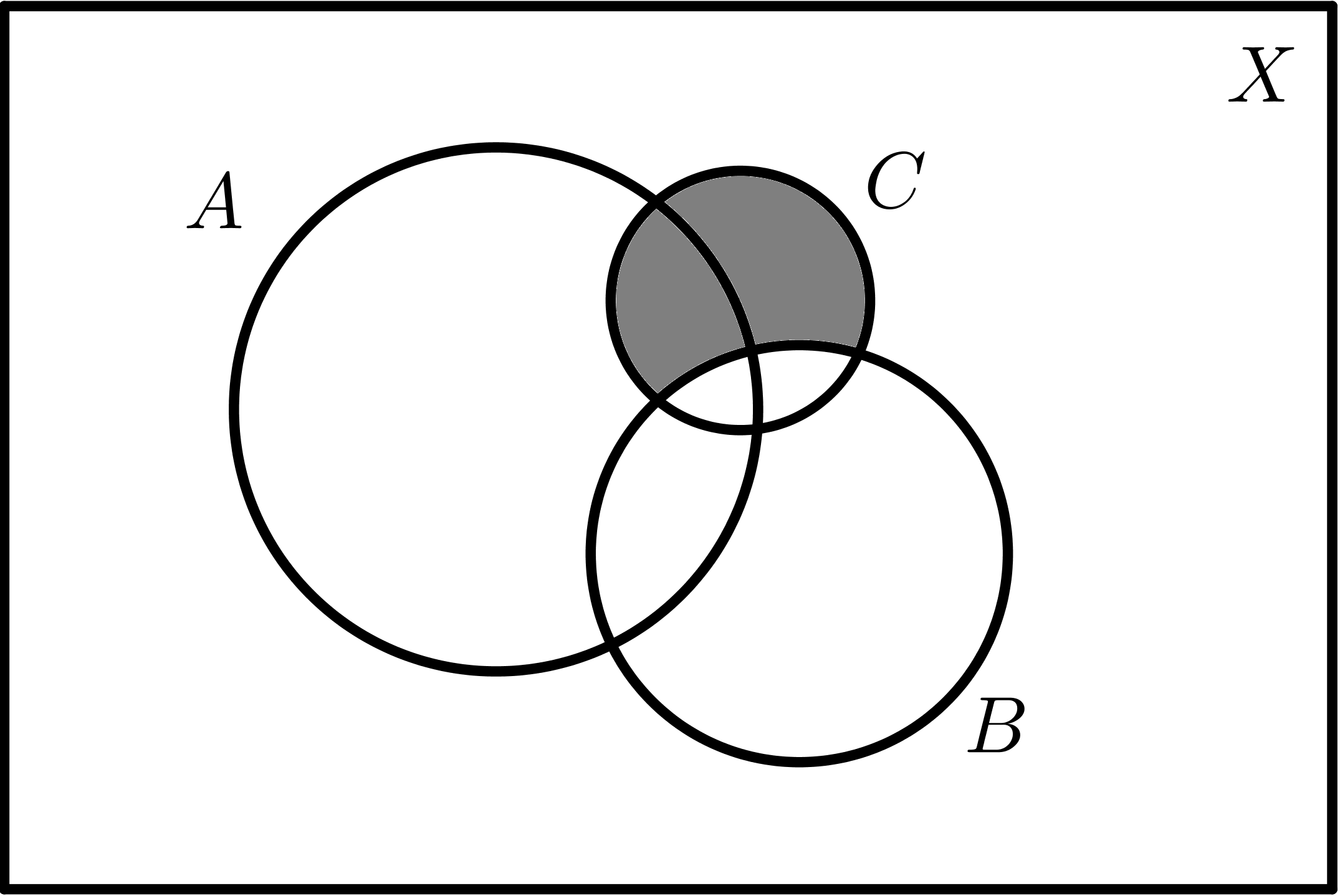
$$C - A$$	$$C - B$$
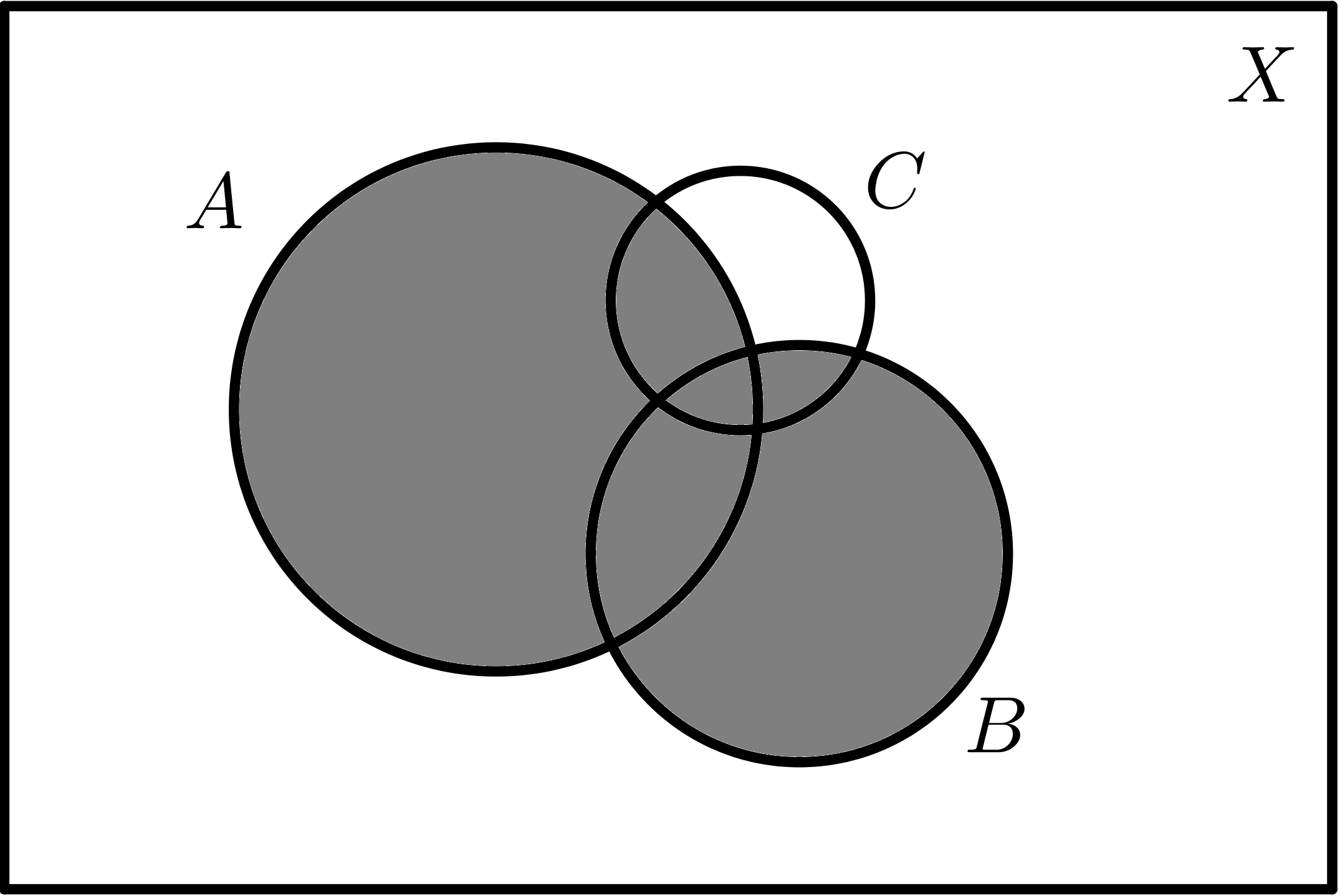
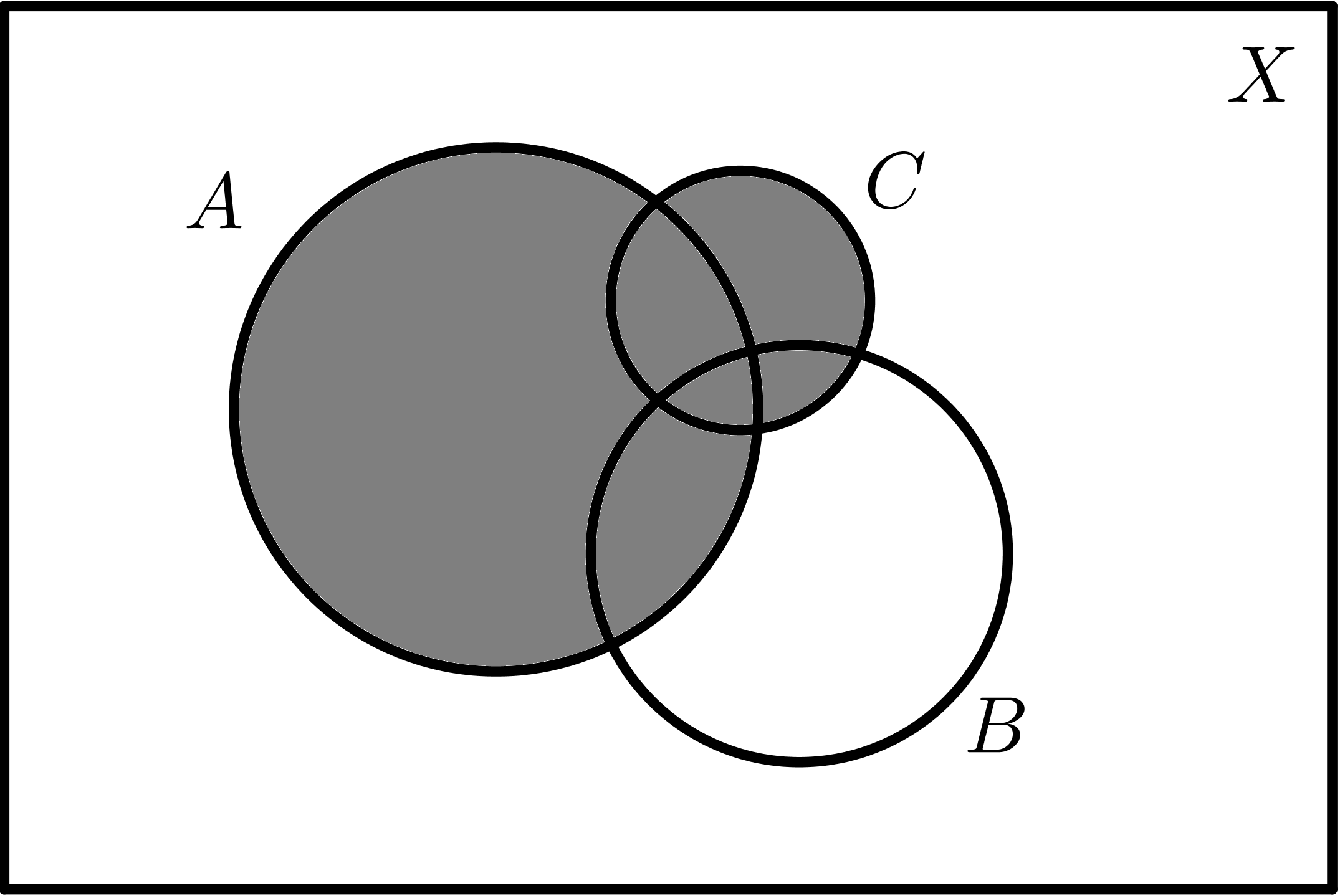
$$A \cup B$$	$$A \cup C$$
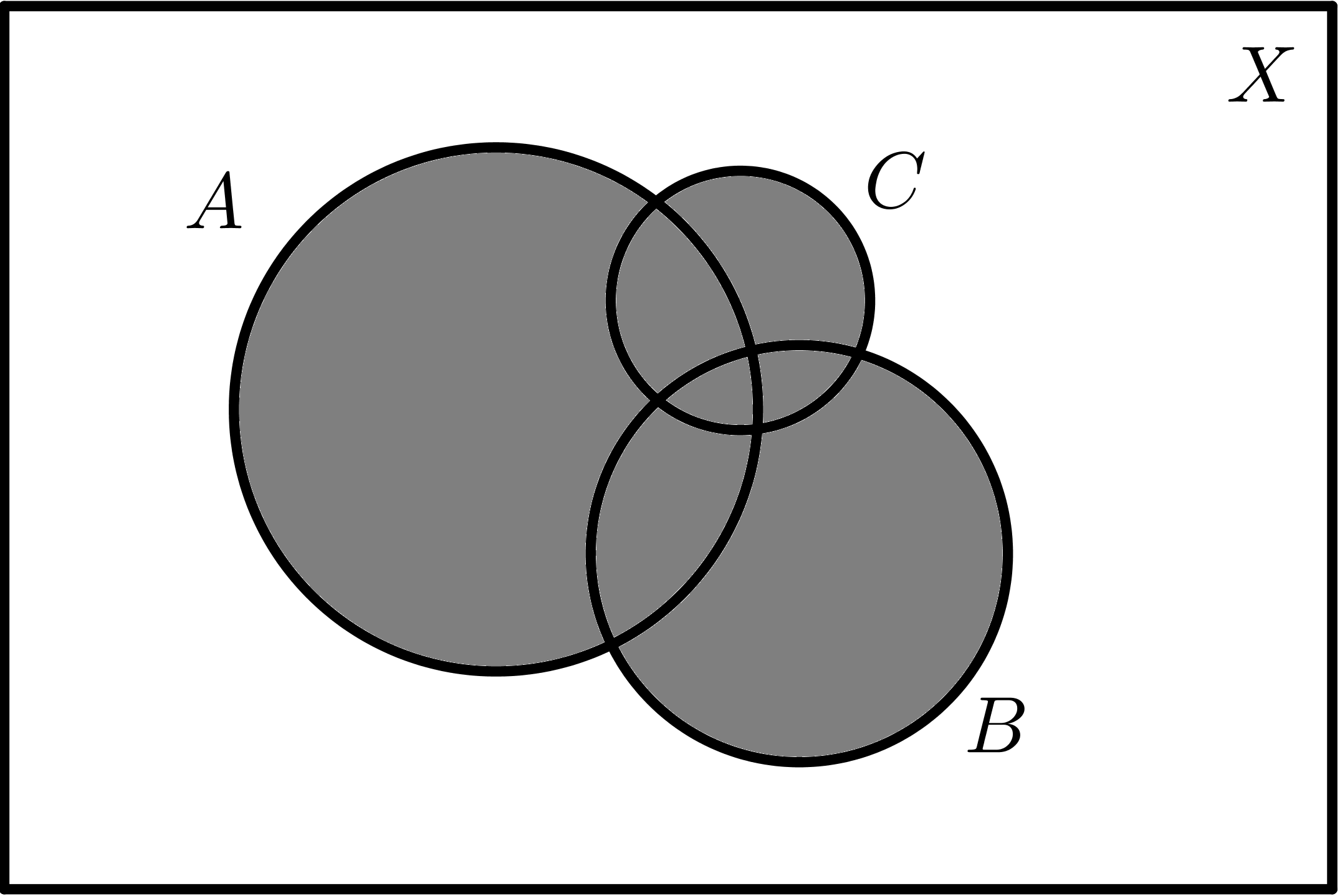
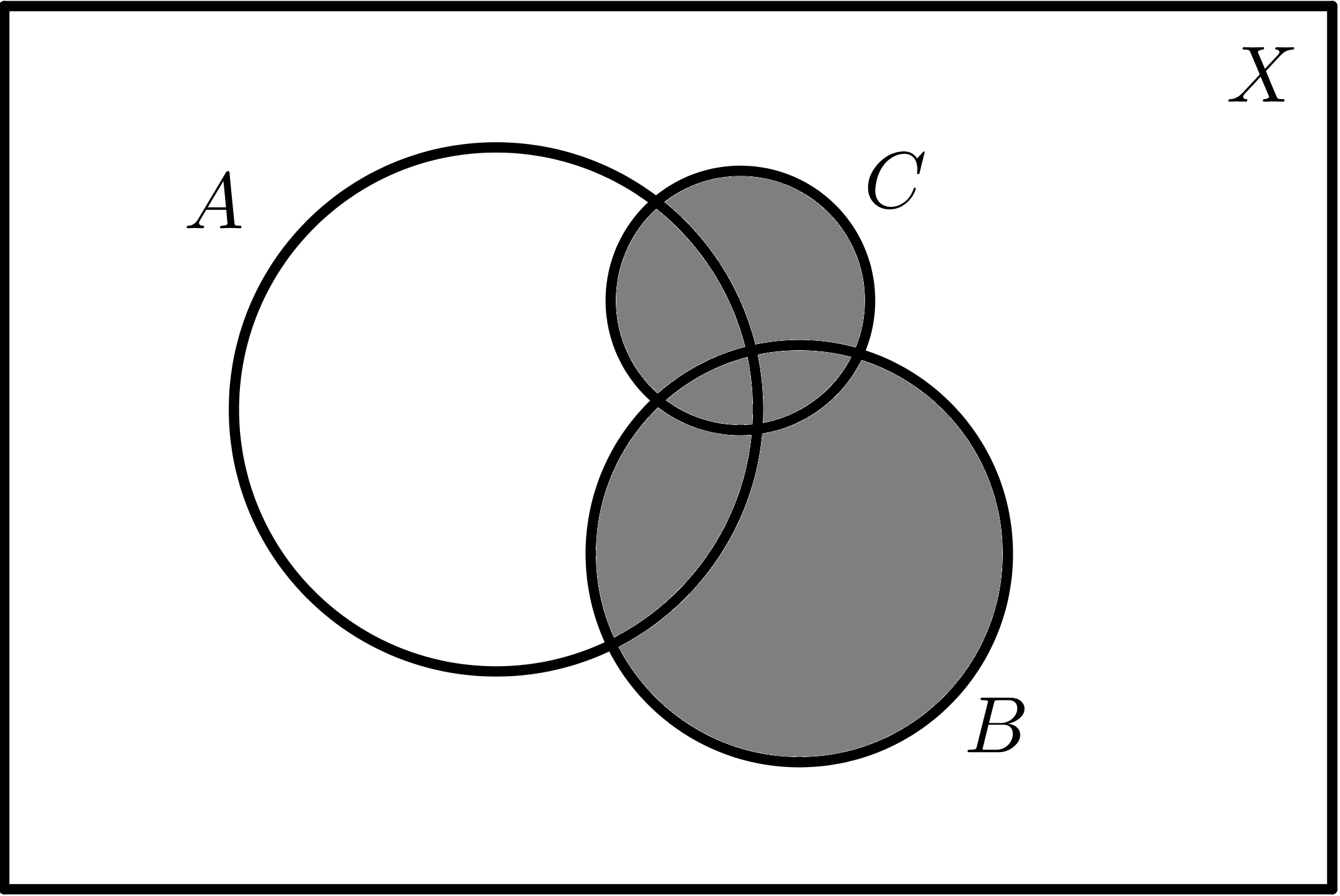
$$B \cup C$$	$$A \cup B \cup C$$
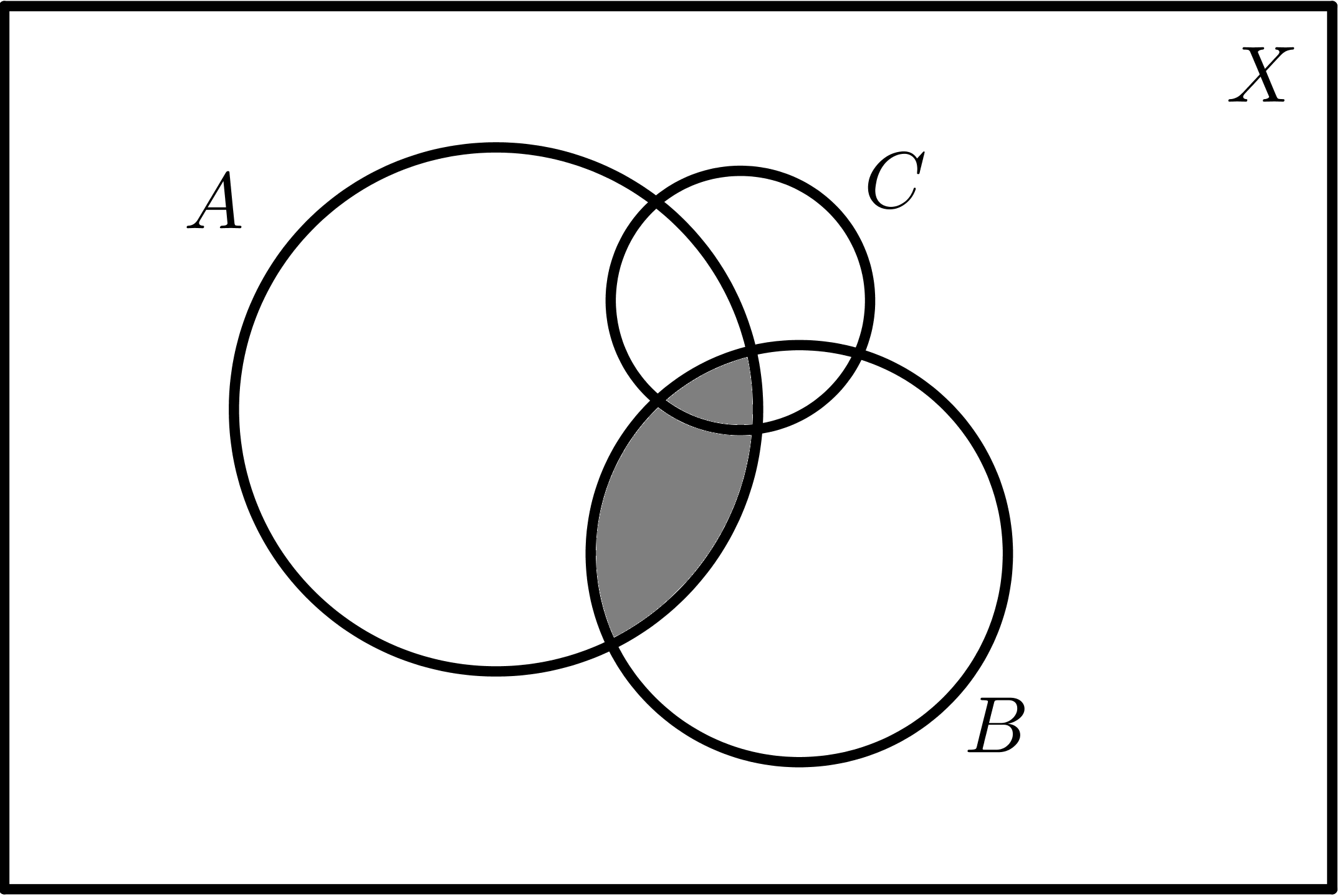
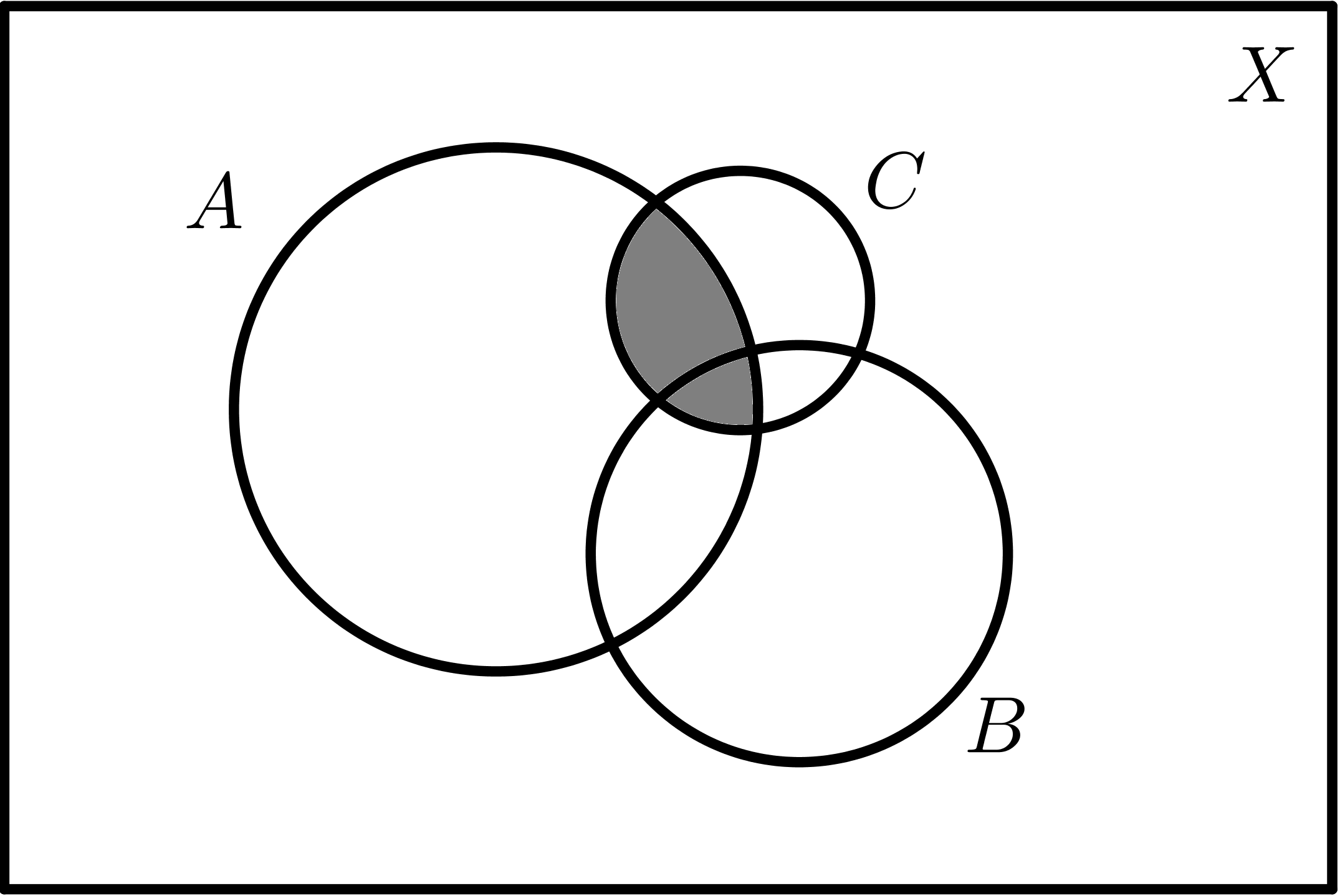
$$A \cap B$$	$$A \cap C$$
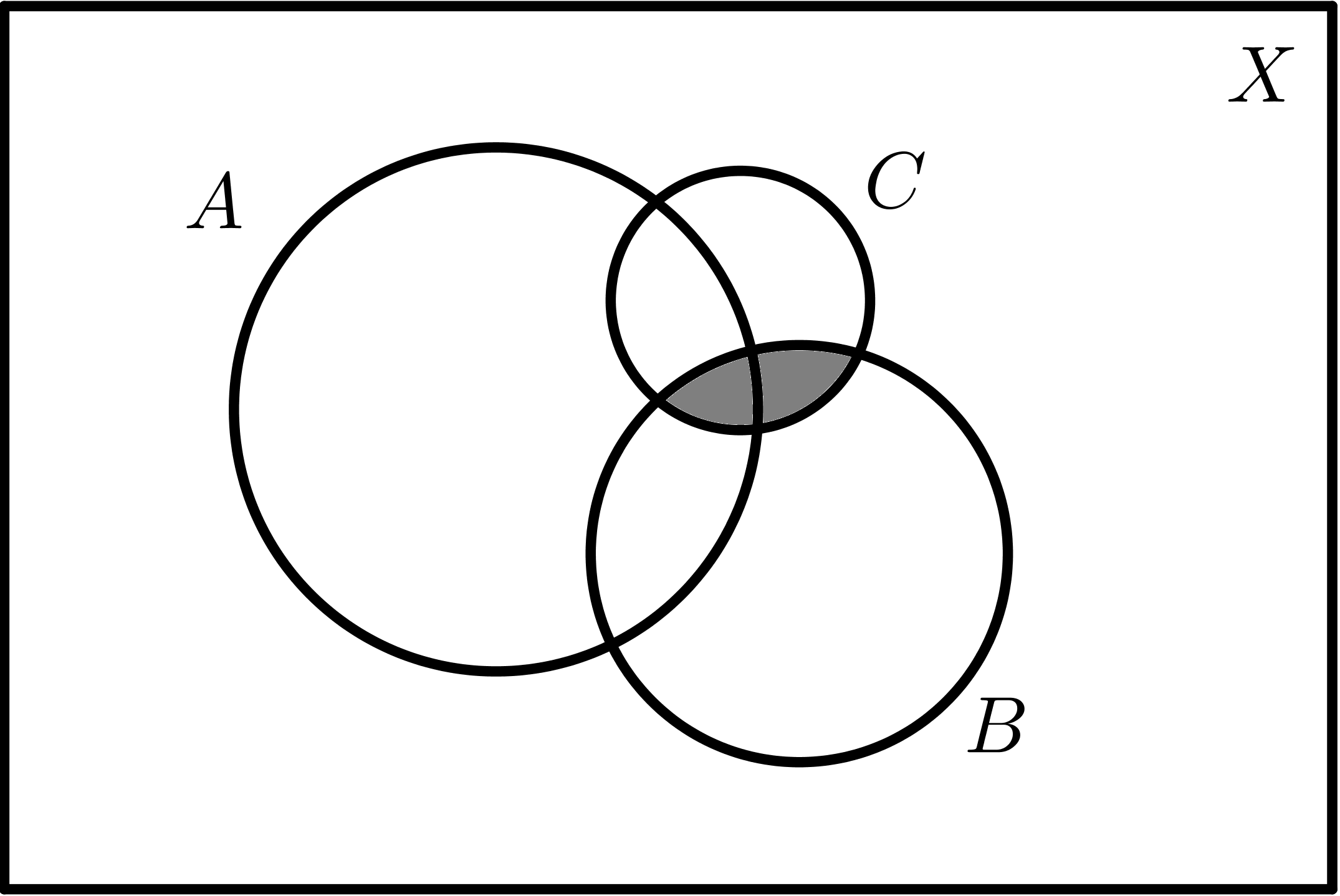
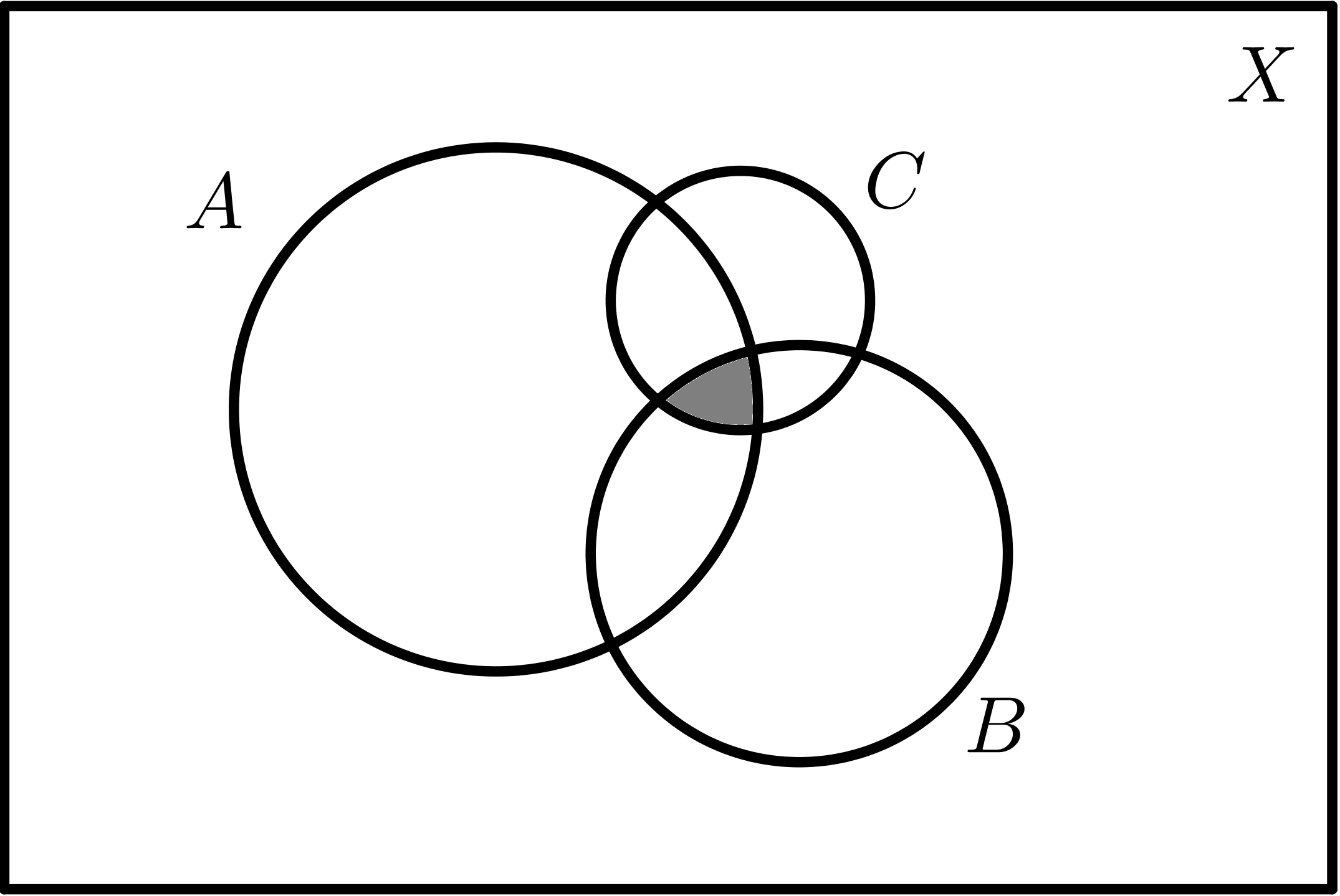
$$B \cap C$$	$$A \cap B \cap C$$