2ºBACH CCSS PROBABILIDAD (PROBLEMAS)
Probabilidad
Problema (#1)
Al lanzar una moneda tres veces se consideran los siguientes sucesos: \(A\):"sacar al menos una cara y una cruz" y \(B\):"sacar a lo sumo una cara".
- Determine el espacio muestral asociado a ese experimento y los sucesos \(A\) y \(B\).
- ¿Son independientes ambos sucesos?
Solución:
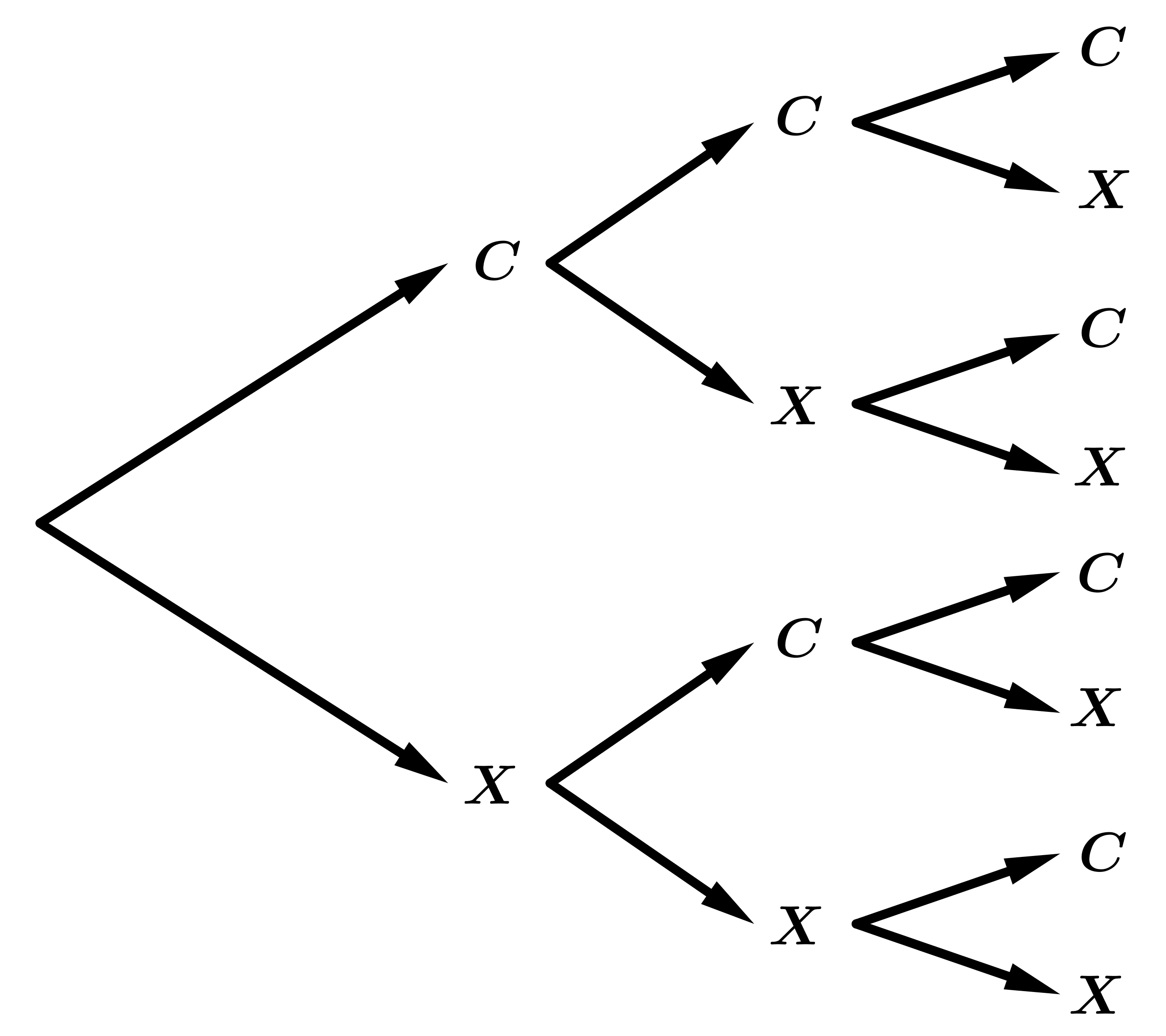
-
A partir del diagrama de árbol, se deduce que:
\(E=\displaystyle{\left\{ccc,ccx,cxc,cxx,xcc,xcx,xxc,xxx\right\}}\)
\(A=\displaystyle{\left\{ccc,ccx,cxc,cxx,xcc,xcx,xxc\right\}}\)
\(B=\displaystyle{\left\{cxx,xcx,xxc,xxx\right\}}\)
-
Para ver si los sucesos \(A\) y \(B\) son independientes, comprobamos si
\(P(A \cap B)=P(A) \cdot P(B)\)
\(A \cap B=\displaystyle{\left\{cxx,xcx,xxc\right\}}\)
Aplicando la regla de Laplace:
\(P(A)=\displaystyle{\frac{7}{8}}\), \(P(B)=\displaystyle{\frac{1}{2}}\) y \(P(A \cap B)=\displaystyle{\frac{3}{8}}\)
\(\left.\begin{array}{c} P(A \cap B)=\displaystyle{\frac{3}{8}}\\ P(A) \cdot P(B)=\displaystyle{\frac{7}{8}} \cdot \displaystyle{\frac{1}{2}}=\displaystyle{\frac{7}{16}}\\ \end{array}\right\} \Rightarrow\)
\( \Rightarrow P(A \cap B) \neq P(A) \cdot P(B)\)
Por tanto, los sucesos \(A\) y \(B\) son dependientes.
Problema (#2)
Dos sucesos \(A\) y \(B\) son tales que \(P(A)=0.30\), \(P\displaystyle{\left(B/A\right)}=0.10\) y \(P\displaystyle{\left(\overline{A \cup B}\right)}=0.63.\)
- ¿Es \(A\) independiente de \(B\)? ¿Es \(B\) independiente de \(A\)?
- Calcule \(P\displaystyle{\left(\overline{A} \cup \overline{B}\right)}\).
Solución:
-
Los sucesos \(A\) y \(B\) son independientes si \(P(A \cap B)=P(A) \cdot P(B)\)
Aplicando la definición de probabilidad condicionada:
\(P(B/A)=0.1\)
\(P(B/A)=\displaystyle{\frac{P(A \cap B)}{P(A)}} \Rightarrow\)
\(\Rightarrow \displaystyle{P(A \cap B)=P(B/A) \cdot P(A)}=\)
\(=0.1 \cdot 0.3 = 0.03 \Rightarrow\)
\(\Rightarrow \displaystyle{P(A \cap B)}=0.03\)
Aplicando la probabilidad del contrario:
\(P\displaystyle{\left(\overline{A \cup B}\right)}=0.63\)
\(P\displaystyle{\left(A \cup B\right)}=1-P\displaystyle{\left(\overline{A \cup B}\right)}=\)
\(=1-0.63=0.37 \Rightarrow\)
\(\Rightarrow P\displaystyle{\left(A \cup B\right)}=0.37\)
De la fórmula de la probabilidad de la unión:
\(P\displaystyle{\left(A \cup B\right)}=P(A)+P(B)-P\displaystyle{\left(A \cap B\right)} \Rightarrow\)
\(\Rightarrow P(B)=P\displaystyle{\left(A \cup B\right)}+P\displaystyle{\left(A \cap B\right)}-P(A) \Rightarrow\)
\(\Rightarrow P(B)=0.37+0.03-0.30=0.10\)
\(\Rightarrow P(B)=0.10\)
Para ver si los sucesos \(A\) y \(B\) son independientes, comprobamos si
\(P(A \cap B)=P(A) \cdot P(B)\):
\(\left.\begin{array}{c} P(A) \cdot P(B)=0.30 \cdot 0.10=0.03\\ P(A \cap B)=0.03\\ \end{array}\right\} \Rightarrow\)
\( \Rightarrow P(A \cap B) = P(A) \cdot P(B)\)
Por tanto, los sucesos \(A\) y \(B\) son independientes.
Aplicando una propiedad de la intersección de conjuntos y la propiedad conmutativa de los números reales:
\(\left.\begin{array}{c} \displaystyle{A \cap B}=\displaystyle{B \cap A}\\ P(A) \cdot P(B)=P(B) \cdot P(A)\\ \end{array}\right\} \Rightarrow\)
\(A\) es independiente de \(B\), si y sólo si \(B\) es independiente de \(A\).
-
Aplicando las leyes de Morgan:
\(P\displaystyle{\left(\overline{A \cup B}\right)}=P\displaystyle{\left(\overline{A} \cap \overline{B}\right)}=0.63\)
\(\left.\begin{array}{c} \displaystyle{P\left(\overline{A}\right)}=1-P(A)=1-0.30=0.70\\ \displaystyle{P\left(\overline{B}\right)}=1-P(B)=1-0.10=0.90 \end{array}\right\} \Rightarrow\)
\(\Rightarrow \left\{\begin{array}{c} \displaystyle{P\left(\overline{A}\right)}=0.70\\ \displaystyle{P\left(\overline{B}\right)}=0.90\\ \end{array}\right.\)
De la fórmula de la probabilidad de la unión:
\(P\displaystyle{\left(\overline{A} \cup \overline{B}\right)}=P\displaystyle{\left(\overline{A}\right)}+P\displaystyle{\left(\overline{B}\right)}-P\displaystyle{\left(\overline{A} \cap \overline{B}\right)}=\)
\(=0.70+0.90-0.63=0.97 \Rightarrow\)
\(\Rightarrow P\displaystyle{\left(\overline{A} \cup \overline{B}\right)}=0.97\)
También podríamos haber resuelto el apartado mediante una tabla de contingencia:
Los datos conocidos de la tabla son los sombreados. Los restantes se obtienen a partir de los otros.
\(\) \(B\) \(\overline{B}\) \(Total\) \(A\) \(0.03\) \(0.27\) \(0.30\) \(\overline{A}\) \(0.07\) \(0.63\) \(0.70\) \(Total\) \(0.10\) \(0.90\) \(1\) Aplicando las leyes de Morgan y la probabilidad del contrario:
\(P\displaystyle{\left(\overline{A} \cup \overline{B}\right)}=P\displaystyle{\left(\overline{A \cap B}\right)}=\)
\(=1-P\displaystyle{\left(A \cap B\right)}=1-0.03=0.97\)
Problema (#3)
Dado el espacio muestral \(E\) se consideran los sucesos \(A\) y \(B\), cuyas probabilidades son \(P(A)=\displaystyle{\frac{2}{3}}\) y \(P(B)=\displaystyle{\frac{1}{2}}.\)
- ¿Pueden ser los sucesos \(A\) y \(B\) incompatibles?
- Suponiendo que los sucesos \(A\) y \(B\) son independientes, calcule \(P\displaystyle{\left(A \cup B\right)}\).
- Suponiendo que \(\displaystyle{A \cup B=E}\), calcule \(P\displaystyle{\left(A \cap B\right)}\).
Solución:
-
Para ver si los sucesos \(A\) y \(B\) son incompatibles, comprobamos si
\(A \cap B=\varnothing \Leftrightarrow P(A \cap B)=0.\)
De la fórmula de la probabilidad de la unión:
\(P\displaystyle{\left(A \cup B\right)}=P(A)+P(B)-P\displaystyle{\left(A \cap B\right)} \Rightarrow\)
\(\left.\begin{array}{c} \varnothing \subseteq \displaystyle{A \cup B} \subseteq X \Rightarrow 0 \leq P\displaystyle{\left(A \cup B\right)} \leq 1\\ P(A)+P(B)=\displaystyle{\frac{2}{3}}+\displaystyle{\frac{1}{2}}=\displaystyle{\frac{7}{6}} \geq 1\\ \end{array}\right\} \Rightarrow\)
\(\Rightarrow P\displaystyle{\left(A \cap B\right)} > 0 \Rightarrow \displaystyle{A \cap B} \neq \varnothing \Rightarrow\)
\(\Rightarrow\) Los sucesos \(A\) y \(B\) son compatibles.
-
Si suponemos que los sucesos \(A\) y \(B\) son independientes:
\(P(A \cap B)=P(A) \cdot P(B) \Rightarrow\)
\(\Rightarrow P(A \cap B)=\displaystyle{\frac{2}{3}} \cdot \displaystyle{\frac{1}{2}}=\displaystyle{\frac{1}{3}} \Rightarrow\)
\(\Rightarrow P(A \cap B)=\displaystyle{\frac{1}{3}}\)
De la fórmula de la probabilidad de la unión:
\(P\displaystyle{\left(A \cup B\right)}=P(A)+P(B)-P\displaystyle{\left(A \cap B\right)} \Rightarrow\)
\(\Rightarrow P\displaystyle{\left(A \cup B\right)}=\displaystyle{\frac{2}{3}}+\displaystyle{\frac{1}{2}}-\displaystyle{\frac{1}{3}}=\displaystyle{\frac{5}{6}} \Rightarrow\)
\(\Rightarrow P\displaystyle{\left(A \cup B\right)}=\displaystyle{\frac{5}{6}}\)
-
Si \(\displaystyle{A \cup B=E} \Rightarrow P\displaystyle{\left(A \cup B\right)}=P(E)=1\)
De la fórmula de la probabilidad de la unión:
\(P\displaystyle{\left(A \cup B\right)}=P(A)+P(B)-P\displaystyle{\left(A \cap B\right)} \Rightarrow\)
\(\Rightarrow P\displaystyle{\left(A \cap B\right)}=P(A)+P(B)-P\displaystyle{\left(A \cup B\right)} \Rightarrow\)
\(\Rightarrow P\displaystyle{\left(A \cap B\right)}=\displaystyle{\frac{2}{3}}+\displaystyle{\frac{1}{2}}-1=\displaystyle{\frac{1}{6}} \Rightarrow\)
\(\Rightarrow P\displaystyle{\left(A \cap B\right)}=\displaystyle{\frac{1}{6}}\)
Problema (#4)
Sean \(A\) y \(B\) dos sucesos tales que \(P(A)=\displaystyle{\frac{1}{2}}\), \(P(B)=\displaystyle{\frac{1}{3}}\) y \(P\displaystyle{\left(A \cap B\right)=\displaystyle{\frac{1}{4}}}\). Calcule:
- \(P\displaystyle{\left(A/B\right)}\) y \(P\displaystyle{\left(B/A\right)}.\)
- Calcule \(P\displaystyle{\left(A \cup B\right)}\).
- Calcule \(P\displaystyle{\left(\overline{A} \cup B\right)}\).
Solución:
-
Aplicando la definición de probabilidad condicionada:
\(P(A/B)=\displaystyle{\frac{P(A \cap B)}{P(B)}}=\displaystyle{\frac{\displaystyle{\frac{1}{4}}}{\displaystyle{\frac{1}{3}}}}=\displaystyle{\frac{3}{4}} \Rightarrow P(A/B)=\displaystyle{\frac{3}{4}}\)
\(P(B/A)=\displaystyle{\frac{P(B \cap A)}{P(A)}}=\displaystyle{\frac{P(A \cap B)}{P(A)}}=\displaystyle{\frac{\displaystyle{\frac{1}{4}}}{\displaystyle{\frac{1}{2}}}}=\displaystyle{\frac{1}{2}} \Rightarrow P(B/A)=\displaystyle{\frac{1}{2}}\)
-
De la fórmula de la probabilidad de la unión:
\(P\displaystyle{\left(A \cup B\right)}=P(A)+P(B)-P\displaystyle{\left(A \cap B\right)}=\displaystyle{\frac{1}{2}}+\displaystyle{\frac{1}{3}}-\displaystyle{\frac{1}{4}}=\displaystyle{\frac{7}{12}} \Rightarrow P\displaystyle{\left(A \cup B\right)}=\displaystyle{\frac{7}{12}}\)
-
\(P\displaystyle{\left(\overline{A} \cup B\right)}=\displaystyle{\frac{1}{12}}\)
Tabla de contingencia: Los datos conocidos de la tabla son los sombreados. Los restantes se obtienen a partir de los otros.
\(\) \(B\) \(\overline{B}\) \(Total\) \(A\) \(\displaystyle{\frac{1}{4}}\) \(\displaystyle{\frac{1}{4}}\) \(\displaystyle{\frac{1}{2}}\) \(\overline{A}\) \(\displaystyle{\frac{1}{12}}\) \(\displaystyle{\frac{5}{12}}\) \(\displaystyle{\frac{1}{2}}\) \(Total\) \(\displaystyle{\frac{1}{3}}\) \(\displaystyle{\frac{2}{3}}\) \(1\)
Problema (#5)
Sean \(A\) y \(B\) dos sucesos del mismo espacio muestral tales que \(P(A)=0.70\), \(P(B)=0.60\) y \(P\displaystyle{\left(A \cup B\right)}=0.90\). Calcule:
- Justifique si \(A\) y \(B\) son independientes.
- Calcule \(P\displaystyle{\left(A/\overline{B}\right)}\) y \(P\displaystyle{\left(B/\overline{A}\right)}.\)
Solución:
-
De la fórmula de la probabilidad de la unión:
\(P\displaystyle{\left(A \cup B\right)}=P(A)+P(B)-P\displaystyle{\left(A \cap B\right)} \Rightarrow\)
\(\Rightarrow P\displaystyle{\left(A \cap B\right)}=P(A)+P(B)-P\displaystyle{\left(A \cup B\right)} \Rightarrow\)
\(\Rightarrow P\displaystyle{\left(A \cap B\right)}=0.70+0.60-0.90=0.40\)
Para ver si los sucesos \(A\) y \(B\) son independientes, comprobamos si
\(P(A \cap B)=P(A) \cdot P(B)\)
\(\left.\begin{array}{c} P(A) \cdot P(B)=0.70 \cdot 0.60=0.42\\ P(A \cap B)=0.40\\ \end{array}\right\} \Rightarrow\) Los sucesos \(A\) y \(B\) son dependientes.
-
Aplicando la definición de probabilidad condicionada:
\(P(A/\overline{B})=\displaystyle{\frac{P(A \cap \overline{B})}{\overline{B}}}=\displaystyle{\frac{0.3}{0.4}}=0.75 \Rightarrow P(A/\overline{B})=0.75\)
\(P(B/\overline{A})=\displaystyle{\frac{P(B \cap \overline{A})}{\overline{A}}}=\displaystyle{\frac{0.2}{0.3}}=0.67 \Rightarrow P(B/\overline{A})=0.67\)
Tabla de contingencia: Los datos conocidos de la tabla son los sombreados. Los restantes se obtienen a partir de los otros.
\(\) \(B\) \(\overline{B}\) \(Total\) \(A\) \(0.40\) \(0.30\) \(0.70\) \(\overline{A}\) \(0.20\) \(0.10\) \(0.30\) \(Total\) \(0.60\) \(0.40\) \(1\)
Problema (#6)
Sean \(A\) y \(B\) dos sucesos aleatorios tales que \(P(A)=0.4\), \(P(B)=0.5\) y \(P\displaystyle{\left(A \cap B\right)}=0.2\).
- Calcule las siguientes probabilidades: \(P\displaystyle{\left(A \cup B\right)}\), \(P\displaystyle{\left(A/B\right)}\) y \(P\displaystyle{\left(B/\overline{A}\right)}.\)
- Razone si \(A\) y \(B\) son sucesos incompatibles.
- Razone si \(A\) y \(B\) son independientes.
Solución:
-
De la fórmula de la probabilidad de la unión:
\(P\displaystyle{\left(A \cup B\right)}=P(A)+P(B)-P\displaystyle{\left(A \cap B\right)} \Rightarrow P\displaystyle{\left(A \cup B\right)}=0.4+0.5-0.2=0.7\)
Aplicando la probabilidad del contrario:
\(P\displaystyle{(A)}=0.40 \Rightarrow P\displaystyle{\left(\overline{A}\right)}=1-P\displaystyle{\left(A\right)}=1-0.40=0.60\)
Aplicando la definición de probabilidad condicionada:
\(P(A/B)=\displaystyle{\frac{P(A \cap B)}{B}}=\displaystyle{\frac{0.20}{0.50}}=0.40 \Rightarrow P(A/B)=0.40\)
\(P(B/\overline{A})=\displaystyle{\frac{P(B \cap \overline{A})}{\overline{A}}}=\displaystyle{\frac{0.30}{0.6}}=0.50 \Rightarrow P(B/\overline{A})=0.50\)
Tabla de contingencia:
Los datos conocidos de la tabla son los sombreados. Los restantes se obtienen a partir de los otros.
\(\) \(B\) \(\overline{B}\) \(Total\) \(A\) \(0.2\) \(0.2\) \(0.4\) \(\overline{A}\) \(0.3\) \(0.3\) \(0.6\) \(Total\) \(0.5\) \(0.5\) \(1\) -
Para ver si los sucesos \(A\) y \(B\) son incompatibles, comprobamos si
\(A \cap B=\varnothing \Leftrightarrow P(A \cap B)=0.\)
\(P(A \cap B)=0.2 \Rightarrow\) Los sucesos \(A\) y \(B\) son compatibles.
-
Para ver si los sucesos \(A\) y \(B\) son independientes, comprobamos si
\(P(A \cap B)=P(A) \cdot P(B)\)
\(\left.\begin{array}{c} P(A) \cdot P(B)=0.40 \cdot 0.50=0.20\\ P(A \cap B)=0.20\\ \end{array}\right\} \Rightarrow\) Los sucesos \(A\) y \(B\) son independientes.
Problema (#7)
Sean dos sucesos, \(A\) y \(B\), tales que \(P(A)=0.5\), \(P(B)=0.4\) y \(P\displaystyle{\left(A/B\right)}=0.5\).
- Halle la probabilidad de que se verifique alguno de los dos sucesos.
- Calcule la probabilidad de que no se verifique \(B\) si se ha verificado \(A\).
- ¿Son independientes los sucesos \(A\) y \(B\)? Razone la respuesta.
Solución:
-
Aplicando la definición de probabilidad condicionada:
\(P(A/B)=0.50 \Rightarrow P(A/B)=\displaystyle{\frac{P(A \cap B)}{P(B)}}=0.50 \Rightarrow\)
\(\Rightarrow \displaystyle{P(A \cap B)=P(B) \cdot P(A/B)}=0.40 \cdot 0.50 = 0.20\)
De la fórmula de la probabilidad de la unión:
\(P\displaystyle{\left(A \cup B\right)}=P(A)+P(B)-P\displaystyle{\left(A \cap B\right)}=0.50+0.40-0.20=0.70 \Rightarrow P\displaystyle{\left(A \cup B\right)}=0.70\)
-
Aplicando la definición de probabilidad condicionada:
\(P(\overline{B}/A)=\displaystyle{\frac{P(\overline{B} \cap A)}{P(A)}}=\displaystyle{\frac{0.30}{0.50}}=0.60 \Rightarrow P(\overline{B}/A)=0.60\)
Tabla de contingencia:
Los datos conocidos de la tabla son los sombreados. Los restantes se obtienen a partir de los otros.
\(\) \(B\) \(\overline{B}\) \(Total\) \(A\) \(0.20\) \(0.30\) \(0.50\) \(\overline{A}\) \(0.20\) \(0.30\) \(0.50\) \(Total\) \(0.40\) \(0.60\) \(1\) -
Para ver si los sucesos \(A\) y \(B\) son independientes, comprobamos si
\(P(A \cap B)=P(A) \cdot P(B)\)
\(\left.\begin{array}{c} P(A) \cdot P(B)=0.50 \cdot 0.40=0.20\\ P(A \cap B)=0.20\\ \end{array}\right\} \Rightarrow\) Los sucesos \(A\) y \(B\) son independientes.
Problema (#8)
En un conjunto de estudiantes, el \(15\%\) estudia alemám, el \(30\%\) estudia francés y el \(10\%\) ambas materias.
- ¿Son independientes los sucesos "estudiar alemán" y "estudiar francés"?
- Si se elige un estudiante al azar, calcule la probabilidad de que no estudie ni francés ni alemán.
Solución:
| \(\) | \(F\) | \(\overline{F}\) | \(Total\) |
|---|---|---|---|
| \(A\) | \(0.10\) | \(0.05\) | \(0.15\) |
| \(\overline{A}\) | \(0.20\) | \(0.65\) | \(0.85\) |
| \(Total\) | \(0.30\) | \(0.70\) | \(1\) |
-
Para ver si los sucesos \(A\) y \(F\) son independientes, comprobamos si
\(P(A \cap F)=P(A) \cdot P(F)\)
\(\left.\begin{array}{c} P(A) \cdot P(F)=0.15 \cdot 0.30=0.45\\ P(A \cap F)=0.10\\ \end{array}\right\} \Rightarrow\)
\( \Rightarrow P(A \cap F) \neq P(A) \cdot P(F)\)
Por tanto, los sucesos \(A\) y \(F\) son dependientes.
- \(P(\overline{A} \cap \overline{F})=0.65\)
Problema (#9)
El \(80\%\) de los alumnos de un I.E.S. son aficionados al fútbol y el \(60\%\) al cine; la mitad de los alumnos de ese I.E.S. lo son a las dos cosas. Se elige un alumno al azar:
- Halle la probabilidad de que no sea aficionado a ninguna de las dos cosas.
- ¿Cuál es la probabilidad de que sea afiniconado al cine sabiendo que no es aficionado al fútbol?
Solución:
| \(\) | \(C\) | \(\overline{C}\) | \(Total\) |
|---|---|---|---|
| \(F\) | \(0.50\) | \(0.30\) | \(0.80\) |
| \(\overline{F}\) | \(0.10\) | \(0.10\) | \(0.20\) |
| \(Total\) | \(0.60\) | \(0.40\) | \(1\) |
- \(P(\overline{F} \cap \overline{C})=0.10\)
- \(\displaystyle{P(C|\overline{F}})=\displaystyle{\frac{P(C \cap \overline{F})}{P(\overline{F})}}=\displaystyle{\frac{0.10}{0.20}}=0.50\)
Problema (#10)
La tabla adjunta muestra los resultados de una encuesta realizada entre varias personas con estudios primarios \((P)\), medios \((M)\) y superiores \((S)\), sobre la pregunta de si fuman \((F)\) o no fuman \((\overline{F})\):
| \(\) | \(P\) | \(M\) | \(S\) |
|---|---|---|---|
| \(F\) | \(190\) | \(120\) | \(12\) |
| \(\overline{F}\) | \(60\) | \(280\) | \(138\) |
- ¿Cuál es la probabilidad de que una persona encuestada con estudios primarios fume? ¿Y si tiene estudios superiores?
- ¿Son independientes los sucesos "tener estudios superiores" y "no fumar"?
- ¿Cuál es la probabilidad de que una persona encuestada que fume no tenga estudios superiores?
Solución:
Calculamos los totales:
| \(\) | \(P\) | \(M\) | \(S\) | \(Total\) |
|---|---|---|---|---|
| \(F\) | \(190\) | \(120\) | \(12\) | \(322\) |
| \(\overline{F}\) | \(60\) | \(280\) | \(138\) | \(478\) |
| \(Total\) | \(250\) | \(400\) | \(150\) | \(n=800\) |
A partir de los datos de la tabla anterior, obtenemos (dividiendo por el total \(n=800\)) la tabla de probabilides:
| \(\) | \(P\) | \(M\) | \(S\) | \(Total\) |
|---|---|---|---|---|
| \(F\) | \(\displaystyle{\frac{190}{800}}\) | \(\displaystyle{\frac{120}{800}}\) | \(\displaystyle{\frac{12}{800}}\) | \(\displaystyle{\frac{322}{800}}\) |
| \(\overline{F}\) | \(\displaystyle{\frac{60}{800}}\) | \(\displaystyle{\frac{280}{800}}\) | \(\displaystyle{\frac{138}{800}}\) | \(\displaystyle{\frac{478}{800}}\) |
| \(Total\) | \(\displaystyle{\frac{250}{800}}\) | \(\displaystyle{\frac{400}{800}}\) | \(\displaystyle{\frac{150}{800}}\) | \(\displaystyle{\frac{800}{800}}\) |
-
\(P(P \cap F)=\displaystyle{\frac{190}{800}}=0.24\) y \(P(S \cap F)=\displaystyle{\frac{12}{800}}=0.02\).
-
Para ver si los sucesos \(S\) y \(\overline{F}\) son independientes, comprobamos si
\(P(S \cap \overline{F})=P(S) \cdot P(\overline{F})\)
\(\left.\begin{array}{c} P(S) \cdot P(\overline{F})=\displaystyle{\frac{150}{800}} \cdot \displaystyle{\frac{478}{800}}=\displaystyle{\frac{717}{6400}}=0.11\\ P(S \cap \overline{F})=\displaystyle{\frac{12}{800}}=0.02\\ \end{array}\right\} \Rightarrow\)
\( \Rightarrow P(S \cap \overline{F}) \neq P(S) \cdot P(\overline{F})\)
Por tanto, los sucesos \(S\) y \(\overline{F}\) son dependientes.
-
Se observa que \(\left.\begin{array}{l} \overline{S}=P \cup M\\ P \cap M=\varnothing\\ \end{array}\right\} \Rightarrow P(P \cup M)=P(P)+P(M)\)
Agrupando los datos en una nueva tabla:
\(\) \(\overline{S}\) \(S\) \(Total\) \(F\) \(\displaystyle{\frac{310}{800}}\) \(\displaystyle{\frac{12}{800}}\) \(\displaystyle{\frac{322}{800}}\) \(\overline{F}\) \(\displaystyle{\frac{340}{800}}\) \(\displaystyle{\frac{138}{800}}\) \(\displaystyle{\frac{478}{800}}\) \(Total\) \(\displaystyle{\frac{650}{800}}\) \(\displaystyle{\frac{150}{800}}\) \(\displaystyle{\frac{800}{800}}\) \(\displaystyle{P(\overline{S}|F})=\displaystyle{\frac{P(\overline{S} \cap F)}{P(F)}}=\displaystyle{\frac{\displaystyle{\frac{310}{800}}}{\displaystyle{\frac{322}{800}}}}=\displaystyle{\frac{310}{322}}=0.96\)
Problema (#11)
De entre los alumnos que cursan 2º curso del Bachillerato de Ciencias de la Salud, el \(80\%\) elige Estadística como optativa y el resto Matemáticas. No hay alumnos que cursen las dos materias a la vez. El \(40\%\) de los alumnos que eligen Estadística supera el curso, mientras de los que eligen Matemáticas el \(55\%\) supera el curso.
- Elegido un alumno al azar, calcule la probabilidad de que supere el curso.
- Si un alumno ha superado el curso, calcule la probabilidad de que haya elegido Estadística.
Solución:
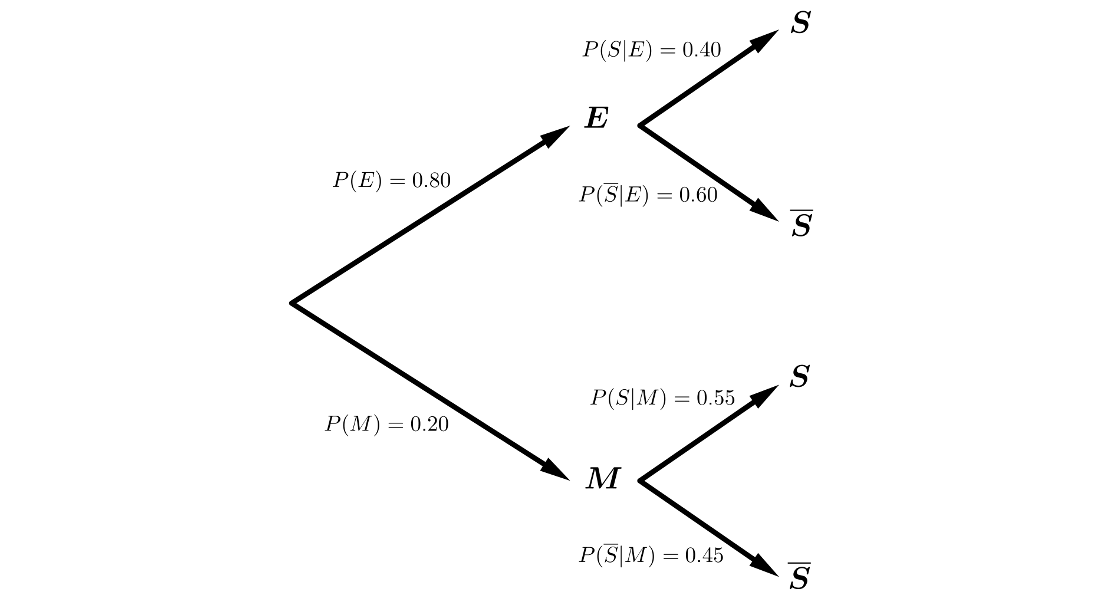
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
-
Aplicando el Teorema de la Probabilidad Total:
\(P(S)=P(E \cap S) + P(M \cap S) =\)
\(= P(E) \cdot P(S|E)+P(M) \cdot P(S|M)=\)
\(=0.80 \cdot 0.40 + 0.20 \cdot 0.55 = 0.43\)
-
Aplicando el Teorema de Bayes:
\(P(E|S)=\displaystyle{\frac{P(E \cap S)}{P(S)}}=\)
\(=\displaystyle{\frac{P(E) \cdot P(S|E)}{P(E) \cdot P(S|E)+P(M) \cdot P(S|M)}}=\)
\(=\displaystyle{\frac{0.80 \cdot 0.40}{0.80 \cdot 0.40 + 0.20 \cdot 0.55}}=\displaystyle{\frac{0.32}{0.43}}=0.74\)
Problema (#12)
En un instituto se ofertan tres modalidades excluyentes \(A\), \(B\) y \(C\) y dos idiomas excluyentes: Inglés y Francés. La modalidad \(A\) es elegida por un \(50\%\) de alumnos, la \(B\) por un \(30\%\) y la \(C\) por un \(20\%\). También se conoce que han elegido Inglés el \(80\%\) de los alumnos de la modalidad \(A\), el \(90\%\) de la modalidad \(B\) y el \(75\%\) de la \(C\), habiendo elegido Francés el resto de los alumnos.
- ¿Qué porcentaje de estudiantes del instituto ha elegido Francés?
- Si se elige al azar un estudiandte de Francés, ¿cuál es la probabilidad de que sea de la modalidad \(A\)?
Solución:
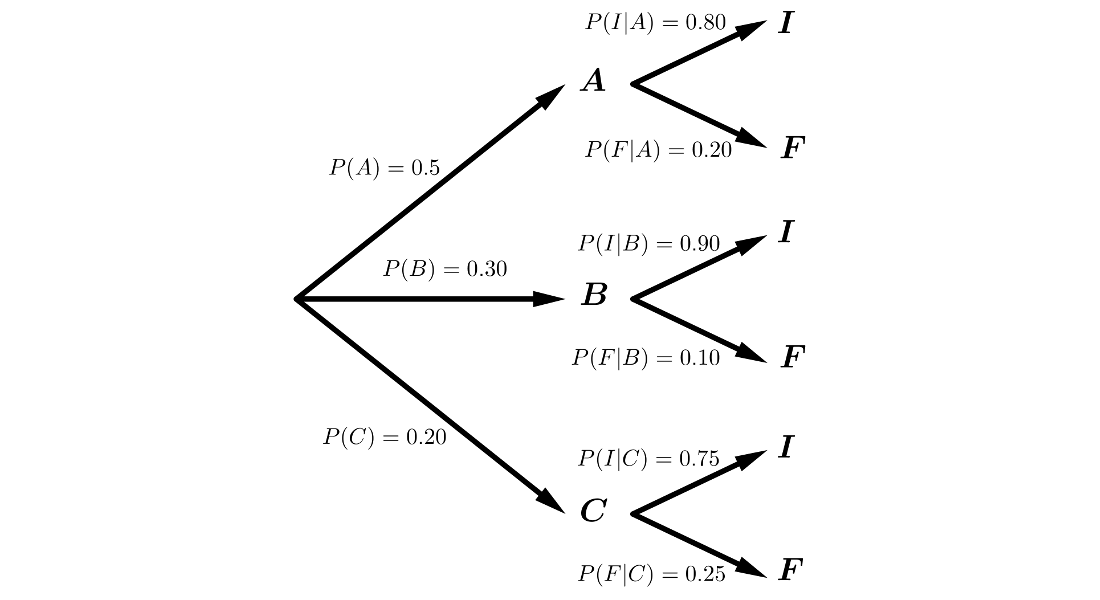
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
-
Aplicando el Teorema de la Probabilidad Total:
\(P(F)=P(A \cap F) + P(B \cap F) + P(C \cap F) =\)
\(=P(A) \cdot P(F|A) + P(B) \cdot P(F|B) + P(C) \cdot P(F|C)=\)
\(=0.50 \cdot 0.20 + 0.30 \cdot 0.10 + 0.20 \cdot 0.25= 0.18\)
-
Aplicando el Teorema de Bayes:
\(P(A|F)=\displaystyle{\frac{P(A \cap F)}{P(F)}}=\)
\(=\displaystyle{\frac{P(A) \cdot P(F|A)}{P(A) \cdot P(F|A) + P(B) \cdot P(F|B) + P(C) \cdot P(F|C)}}=\)
\(=\displaystyle{\frac{0.50 \cdot 0.20}{0.50 \cdot 0.20 + 0.30 \cdot 0.10 + 0.20 \cdot 0.25}}=\)
\(=\displaystyle{\frac{0.10}{0.18}}=0.56\)
Problema (#13)
Un ladrón, al huir de un policia, puede hacerlo por las calles \(A\), \(B\) ó \(C\), con las siguientes probabilidades \(P(A)=0.25\), \(P(B)=0.6\) y \(P(C)=0.15\). La probabilidad de ser alcanzado si huye por la calle \(A\) es \(0.4\), si huye por la calle \(B\) es \(0.5\), y si huye por la \(C\) es 0.6.
- Halle la probabilidad de que el policia alcance al ladrón.
- Si el ladrón ha sido alcanzado, ¿cuál es la probabilidad de que haya sido alcanzado en la calle \(A\)?
Solución:
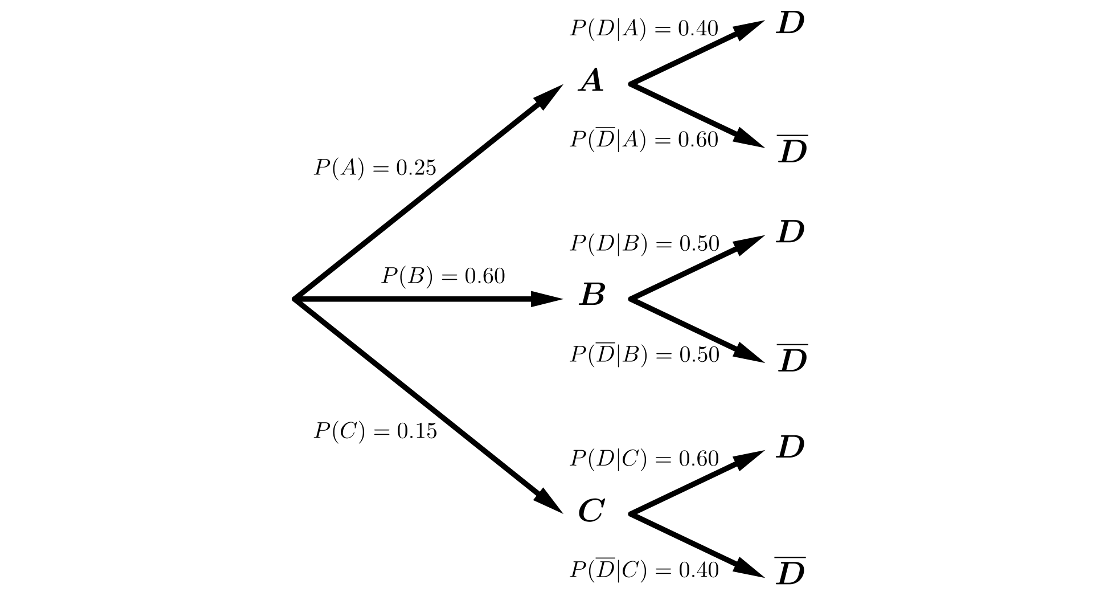
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
Consideremos los sucesos \(D=\)"Ser alcanzado por la policia" y \(\overline{D}=\)"No ser alcanzado por la policia".
-
Aplicando el Teorema de la Probabilidad Total:
\(P(D)=P(A \cap D) + P(B \cap D) + P(C \cap D) =\)
\(=P(A) \cdot P(D|A) + P(B) \cdot P(D|B) + P(C) \cdot P(D|C)=\)
\(=0.25 \cdot 0.40 + 0.60 \cdot 0.50 + 0.15 \cdot 0.60= 0.49\)
-
Aplicando el Teorema de Bayes:
\(P(A|D)=\displaystyle{\frac{P(A \cap D)}{P(D)}}=\)
\(=\displaystyle{\frac{P(A) \cdot P(D|A)}{P(A) \cdot P(D|A) + P(B) \cdot P(D|B) + P(C) \cdot P(D|C)}}=\)
\(=\displaystyle{\frac{0.25 \cdot 0.40}{0.25 \cdot 0.40 + 0.60 \cdot 0.50 + 0.15 \cdot 0.60}}=\displaystyle{\frac{0.10}{0.49}}=0.20\)
Problema (#14)
La población española está compuesta por un \(55\%\) de mujeres, de las que un \(8\%\) ha realizado en alguna ocasión una compra por Internet. Se sabe que la probabilidad de que una persona haya comprado alguna vez usando Internet es 0.3.
- Halle la probabilidad de que un hombre, elegido al azar, haya comprado alguna vez por Internet.
Solución:
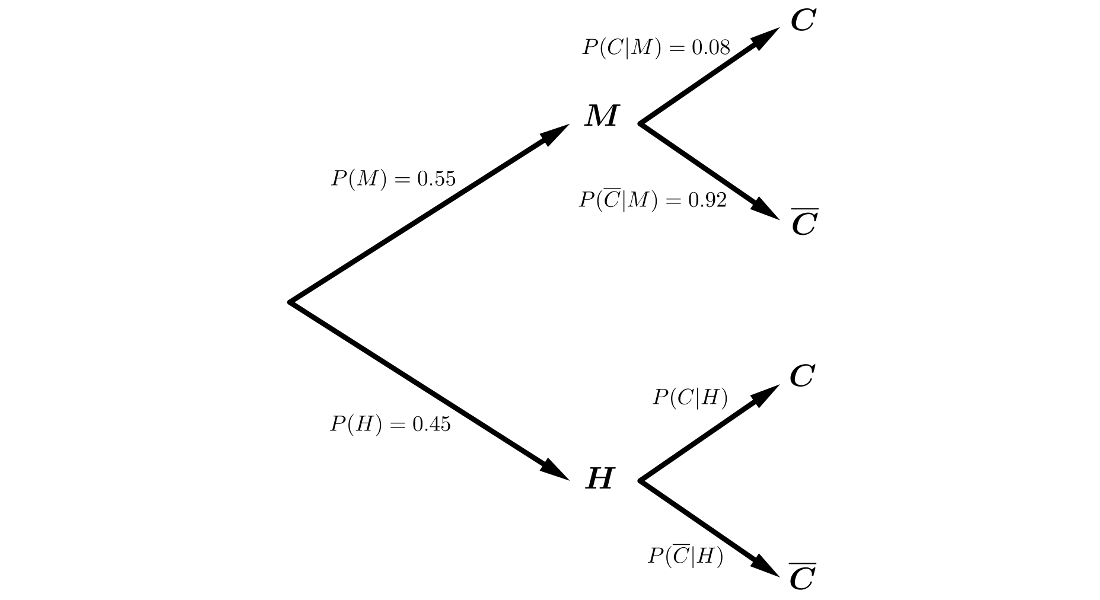
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
-
Aplicando el Teorema de la Probabilidad Total:
\(P(C)=P(M \cap C) + P(H \cap C) =\)
\(= P(M) \cdot P(C|M)+P(H) \cdot P(C|H) \Rightarrow\)
\(\Rightarrow 0.3=0.55 \cdot 0.08 + 0.45 \cdot P(C|H) \Rightarrow\)
\(\Rightarrow P(C|H) = \displaystyle{\frac{0.3 - 0.55 \cdot 0.08}{0.45}}=\displaystyle{\frac{0.26}{0.45}}=0.57\)
Aplicando el Teorema de Bayes:
\(P(C|H)=\displaystyle{\frac{P(C \cap H)}{P(H)}}=\)
\(=\displaystyle{\frac{P(H) \cdot P(C|H)}{P(M) \cdot P(C|M)+P(H) \cdot P(C|H)}}=\)
\(=\displaystyle{\frac{0.45 \cdot 0.57}{0.55 \cdot 0.08 + 0.45 \cdot 0.57}}=\)
\(=\displaystyle{\frac{0.26}{0.30}}=0.87\)
Problema (#15)
Tenemos dos urnas \(A\) y \(B\) que contienen las siguientes bolas: A (5 blancas, 3 negras y 2 rojas) y B (4 blancas y 6 negras). También tenemos un dado que tiene 4 caras marcadas con la letra A y las otras dos con la letra B. Tiramos el dado y sacamos una bola al azar de la urna que indica el dado.
- ¿Cuál es la probabilidad de que esa bola sea blanca?
- ¿Cuál es la probabilidad de que esa bola sea roja?
- La bola extraída ha resultado ser blanca: ¿cuál es la probabilidad de que proceda de la urna B?
Solución:
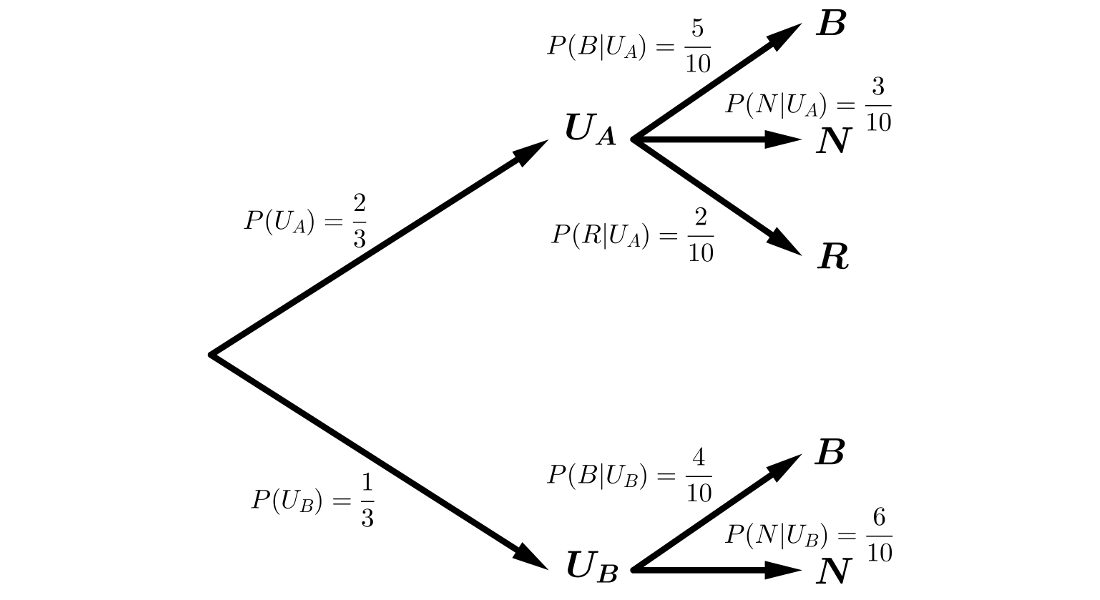
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
Teniendo en cuenta el número de caras del dado con la letra \(A\) y con la letra \(B\), aplicando la regla de Laplace:
$$\left\{\begin{array}{l} P(U_{A})=\displaystyle{\frac{4}{6}}=\displaystyle{\frac{2}{3}}\\ P(U_{B})=\displaystyle{\frac{2}{6}}=\displaystyle{\frac{1}{3}}\\ \end{array}\right.$$
-
Aplicando el Teorema de la Probabilidad Total:
\(P(B)=P(U_{A} \cap B) + P(U_{B} \cap B) = P(U_{A}) \cdot P(B|U_{A}) + P(U_{B}) \cdot P(B|U_{B})=\)
\(=\displaystyle{\frac{2}{3}} \cdot \displaystyle{\frac{5}{10}} + \displaystyle{\frac{1}{3}} \cdot \displaystyle{\frac{4}{10}} = \displaystyle{\frac{10}{30}} + \displaystyle{\frac{4}{30}} = \displaystyle{\frac{14}{30}} = \displaystyle{\frac{7}{15}} = 0.47\)
-
Aplicando el Teorema de la Probabilidad Total:
\(P(R)=P(U_{A} \cap R) = P(U_{A}) \cdot P(R|U_{A}) = \displaystyle{\frac{2}{3}} \cdot \displaystyle{\frac{2}{10}} = \displaystyle{\frac{4}{30}} = \displaystyle{\frac{2}{15}} = 0.13\)
-
Aplicando el Teorema de Bayes:
\(P(U_{B}|B)=\displaystyle{\frac{P(U_{B} \cap B)}{P(B)}}=\displaystyle{\frac{P(U_{B}) \cdot P(B|U_{B})}{P(U_{A}) \cdot P(B|U_{A}) + P(U_{B}) \cdot P(B|U_{B})}}=\)
\(=\displaystyle{\frac{\displaystyle{\frac{1}{3}} \cdot \displaystyle{\frac{4}{10}}}{\displaystyle{\frac{2}{3}} \cdot \displaystyle{\frac{5}{10}} + \displaystyle{\frac{1}{3}} \cdot \displaystyle{\frac{4}{10}}}}=\displaystyle{\frac{\displaystyle{\frac{4}{30}}}{\displaystyle{\frac{10}{30}} + \displaystyle{\frac{4}{30}}}}=\displaystyle{\frac{\displaystyle{\frac{4}{30}}}{\displaystyle{\frac{14}{30}}}}=\displaystyle{\frac{4}{14}}=0.29\)
Problema (#16)
Disponemos de dos dados, uno de los cuales está trucado. La probabilidad de sacar un cinco en el trucado es 0.25, siendo los otros resultados equiprobables. Se elige un dado al azar y se realiza un lanzamiento con él.
- Determine la probabilidad de obtener un dos.
- Dado que ha salido un dos, ¿cuál es la probabilidad de que hayamos elegido el dado trucado?
Solución:
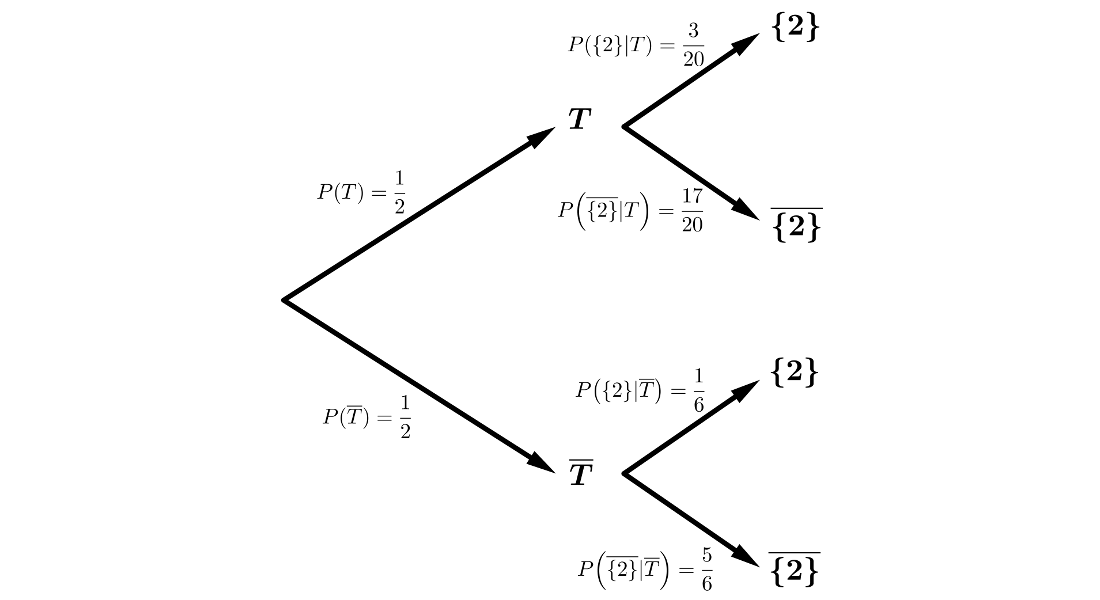
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
Consideremos los sucesos \(T=\)"Dado trucado" y \(\overline{T}=\)"Dado no trucado".
En el dado trucado, la \(P\displaystyle{\left(\{5\}\right)}=0.25=\displaystyle{\frac{1}{4}}\), siendo la del resto de sucesos elementales equiprobables. Por tanto:
Aplicando la probabilidad del contrario:
En el dado trucado, la \(P\displaystyle{\left(\overline{\{5\}}\right)}=1-\displaystyle{P\left(\{5\}\right)}=1-\displaystyle{\frac{1}{4}}=\displaystyle{\frac{3}{4}}\)
Como el resto de sucesos elementales son equiprobables:
\(P(\{1\})=P(\{2\})=P(\{3\})=P(\{4\})=P(\{6\})=\displaystyle{\frac{\displaystyle{\frac{3}{4}}}{5}}=\displaystyle{\frac{3}{20}}\)
En el dado no trucado, todos los sucesos elementales equiprobables. Por tanto:
\(P(\{1\})=P(\{2\})=P(\{3\})=P(\{4\})=P(\{5\})=P(\{6\})=\displaystyle{\frac{1}{6}}\)
-
Aplicando el Teorema de la Probabilidad Total:
\(P(\{2\})=P(T \cap \{2\}) + P(\overline{T} \cap \{2\}) = P(T) \cdot P(T|\{2\})+P(\overline{T}) \cdot P(\overline{T}|\{2\})=\)
\(=\displaystyle{\frac{1}{2}} \cdot \displaystyle{\frac{3}{20}} + \displaystyle{\frac{1}{2}} \cdot \displaystyle{\frac{1}{6}} = \displaystyle{\frac{19}{120}}=0.16\)
-
Aplicando el Teorema de Bayes:
\(P(T|\{2\})=\displaystyle{\frac{P(T \cap \{2\})}{P(\{2\})}}=\displaystyle{\frac{P(T) \cdot P(\{2\}|T)}{P(T) \cdot P(\{2\}|T)+P(\overline{T}) \cdot P(\{2\}|\overline{T})}}=\)
\(=\displaystyle{\frac{\displaystyle{\frac{1}{2}} \cdot \displaystyle{\frac{3}{20}}}{\displaystyle{\frac{1}{2}} \cdot \displaystyle{\frac{3}{20}} + \displaystyle{\frac{1}{2}} \cdot \displaystyle{\frac{1}{6}}}}=\displaystyle{\frac{\displaystyle{\frac{3}{40}}}{\displaystyle{\frac{3}{40}} + \displaystyle{\frac{1}{12}}}}=\displaystyle{\frac{\displaystyle{\frac{3}{40}}}{\displaystyle{\frac{19}{120}}}}=\displaystyle{\frac{9}{19}}=0.47\)
Problema (#17)
De una lista de \(10\) personas, de las que \(7\) son hombres, seleccionamos \(2\) personas al azar. Calcula la probabilidad de que sean de distinto sexo en los siguientes casos:
- Se eligen sin reemplazo.
- Se eligen con reemplazo.
Solución:
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
Consideremos los sucesos \(D=\)"Ser de distinto sexo".
-
Se eligen sin reemplazo.
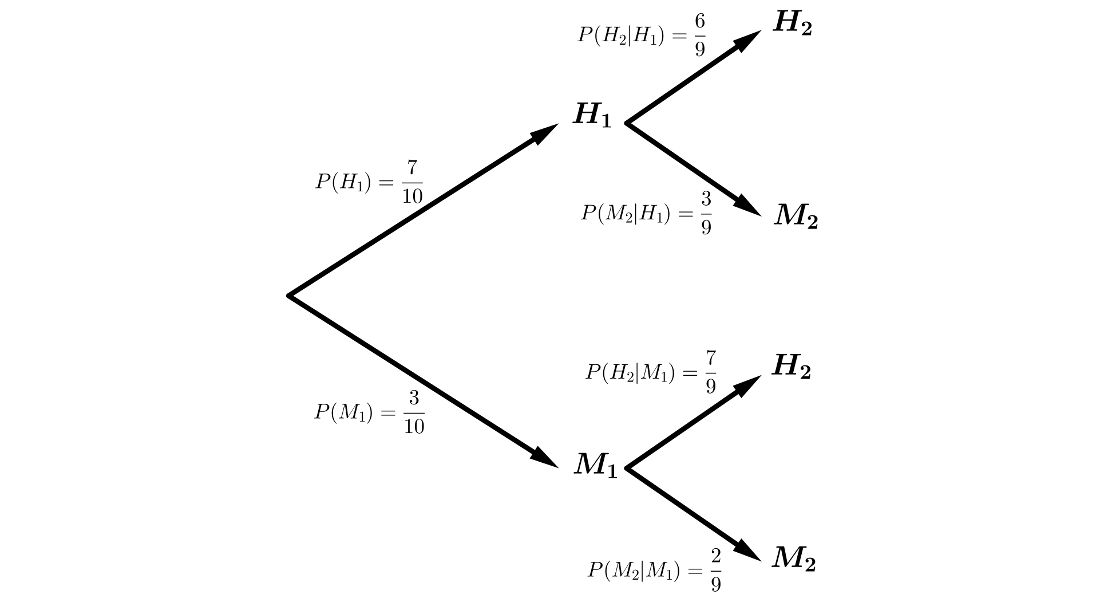
Aplicando el Teorema de la Probabilidad Total:
\(P(D)=P(H_1 \cap M_2) + P(M_1 \cap H_2) = P(H_1) \cdot P(M_2|H_1)+P(M_1) \cdot P(H_2|M_1)=\)
\(=\displaystyle{\frac{7}{10}} \cdot \displaystyle{\frac{3}{9}} + \displaystyle{\frac{3}{10}} \cdot \displaystyle{\frac{6}{9}} = \displaystyle{\frac{39}{90}}= \displaystyle{\frac{13}{30}}=0.43\)
-
Se eligen con reemplazo.
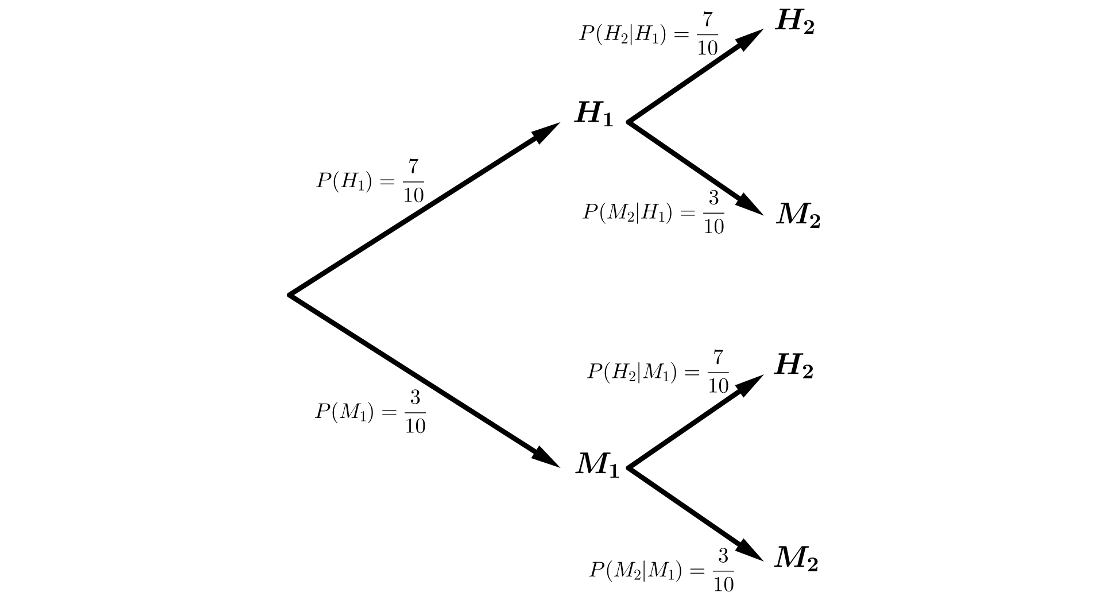
Aplicando el Teorema de la Probabilidad Total:
\(P(D)=P(H_1 \cap M_2) + P(M_1 \cap H_2) = P(H_1) \cdot P(M_2|H_1)+P(M_1) \cdot P(H_2|M_1)=\)
\(=\displaystyle{\frac{7}{10}} \cdot \displaystyle{\frac{3}{10}} + \displaystyle{\frac{3}{10}} \cdot \displaystyle{\frac{7}{10}} = \displaystyle{\frac{42}{100}}= \displaystyle{\frac{21}{50}}=0.42\)
Problema (#18)
En un famoso concurso de televisión basta con responder acertadamente a \(15\) preguntas para ganar \(50\) millones de pesetas. Cada pregunta tiene \(4\) posibles respuestas, de las que sólo una es verdadera.
- Determine la probabilidad de que un concursante que no sabe ninguna pregunta y responde al azar pueda ganar los \(50\) millones.
- Determine la probabilidad de que un concursante con cultura media que sólo conoce las respuestas correctas de las \(5\) primeras, acierte las respuestas de las \(10\) últimas, si éstas las contesta al azar.
Solución:
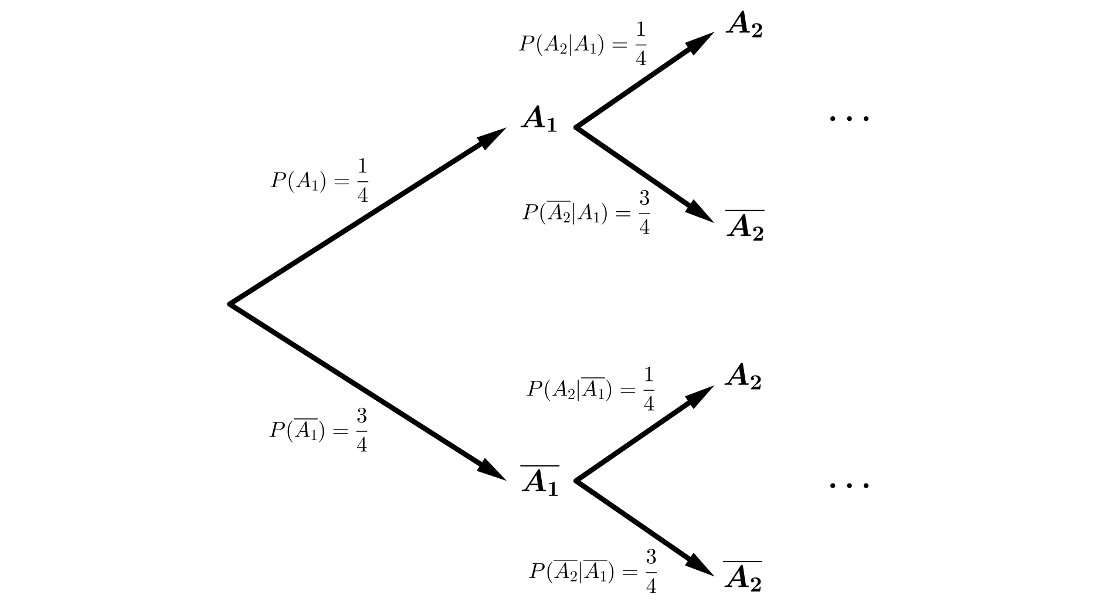
Como cada pregunta tiene 4 posibles respuestas de las que sólo 1 es correcta, aplicando la regla de Laplace:
$$\left.\begin{array}{l} P(A_1)= \cdots = P(A_{15})=\displaystyle{\frac{1}{4}}\\ P(\overline{A_1})= \cdots = P(\overline{A_{15}})=\displaystyle{\frac{3}{4}}\\ \end{array}\right\}$$
-
Aplicando la probabilidad de la intersección:
\(P(A_1 \cap A_2 \cap \cdots \cap A_{15})=\)
\(=P(A_1) \cdot P(A_2|A_1) \cdots P(A_{15}|A_1 \cap A_2 \cap \cdots \cap A_{14})=\)
\(=\displaystyle{\left(\frac{1}{4}\right)^{15}}=9.31 \cdot 10^{-10}\)
-
Aplicando la definición de probabilidad condicionada:
\(P(A_6 \cap \cdots \cap A_{15}|A_1 \cap \cdots \cap A_5) =\)
\(=\displaystyle{\frac{P(A_1 \cap \cdots \cap A_{15})}{P(A_1 \cap \cdots \cap A_5)}}=\)
\(=\displaystyle{\frac{\displaystyle{\left(\frac{1}{4}\right)^{15}}}{\displaystyle{\left(\frac{1}{4}\right)^{5}}}}=\displaystyle{\left(\frac{1}{4}\right)^{10}}=9.54 \cdot 10^{-7}\)
Problema (#19)
En una primera bolsa se han colocado \(4\) bolas blancas y \(3\) negras, y en una segunda bolsa \(3\) blancas y \(5\) negras. Se saca una bola de la primera y, sin verla, se introduce en la segunda. A continuación se saca una bola de la segunda. Halle la probabilidad de que:
- La bola extraída de la segunda bolsa sea negra.
- La bola extraída de la primera bolsa sea negra, si sabemos que la bola extraída de la segunda ha sido blanca.
Solución:
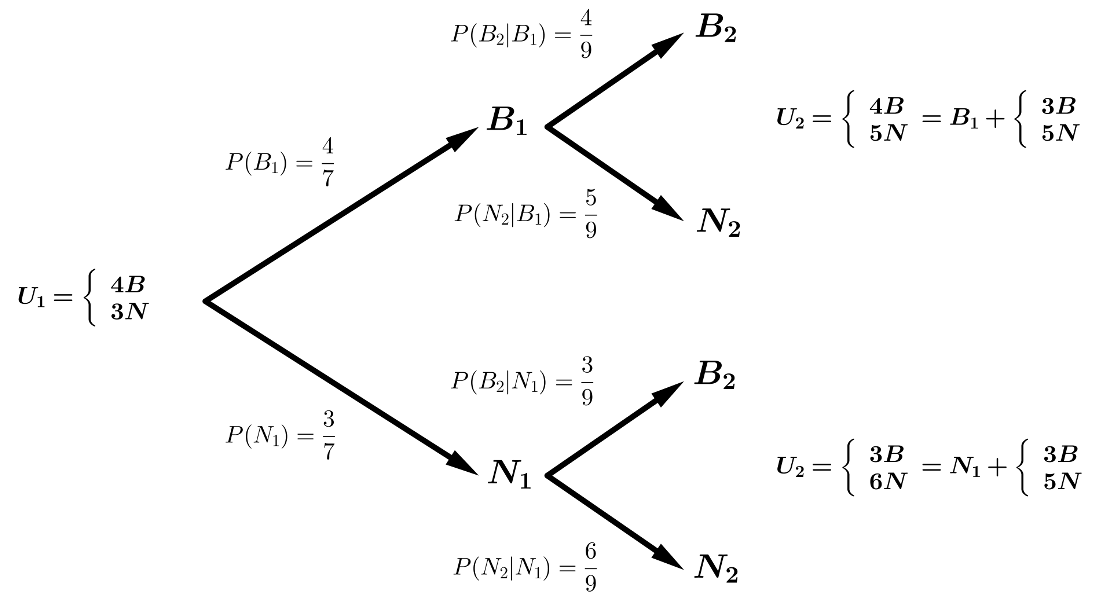
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
-
Aplicando el Teorema de la Probabilidad Total:
\(P(N_2)=P(B_1 \cap N_2) + P(N_1 \cap N_2) = \)
\(=P(B_1) \cdot P(N_2|B_1)+P(N_1) \cdot P(B_2|N_1)=\)
\(=\displaystyle{\frac{4}{7}} \cdot \displaystyle{\frac{5}{9}} + \displaystyle{\frac{3}{7}} \cdot \displaystyle{\frac{6}{9}} = \displaystyle{\frac{38}{63}} = 0.60\)
-
Aplicando el Teorema de Bayes:
\(P(N_1|B_2)=\displaystyle{\frac{P(N_1 \cap B_2)}{P(B_2)}}=\)
\(=\displaystyle{\frac{P(B_1) \cdot P(B_2|N_1)}{P(B_1) \cdot P(B_2|B_1)+P(N_1) \cdot P(B_2|N_1)}}=\)
\(=\displaystyle{\frac{\displaystyle{\frac{3}{7}} \cdot \displaystyle{\frac{3}{9}}}{\displaystyle{\frac{4}{7}} \cdot \displaystyle{\frac{4}{9}} + \displaystyle{\frac{3}{7}} \cdot \displaystyle{\frac{3}{9}}}}=\displaystyle{\frac{\displaystyle{\frac{9}{63}}}{\displaystyle{\frac{25}{63}}}}=\displaystyle{\frac{9}{25}} = 0.36\)
Obtenemos la \(P(B_2)\) aplicando el Teorema de la Probabilidad Total:
\(P(B_2)=P(B_1 \cap B_2) + P(N_1 \cap B_2) =\)
\(= P(B_1) \cdot P(B_2|B_1)+P(N_1) \cdot P(B_2|N_1) =\)
\(= \displaystyle{\frac{4}{7}} \cdot \displaystyle{\frac{4}{9}} + \displaystyle{\frac{3}{7}} \cdot \displaystyle{\frac{3}{9}} = \displaystyle{\frac{25}{63}} = 0.40\)
También podemos obtener la \(P(B_2)\) aplicando la probabilidad del contrario:
\(P(B_2)=1-P(N_2)=1-0.60=0.40\)
Problema (#20)
En una clase el \(60\%\) de los alumnos aprobó Historia y la mitad de la clase aprobó Inglés. Se sabe que el \(70\%\) de los alumnos que aprobaron Historia aprobó Inglés.
- Halle la probabilidad de que un alumno cualquiera de la citada clase apruebe al menos una de las dos asignaturas.
- Calcule el porcentaje de los alumnos que, habiendo aprobado Inglés, aprueban Historia.
- ¿Son independientes los sucesos “aprobar Historia” y “aprobar Inglés”? Razone la respuesta.
Solución:
Los datos de los que disponemos son la \(P(H)=0.60, P(I)=0.50\) y \(P(I|H)=0.70\)
-
Aplicando la probabilidad de la intersección:
\(P(H \cap I)=P(H) \cdot P(I|H)=0.60 \cdot 0.70 = 0.42\)
Aplicando la probabilidad de la unión:
\(P(H \cup I)=P(H)+P(I)-P(H \cap I) =\)
\(=0.60+0.50-0.42=0.68 \Rightarrow\)
\(\Rightarrow P(H \cup I)=0.68\)
-
Aplicando la definición de probabilidad condicionada:
\(P(H|I)=\displaystyle{\frac{P(H \cap I)}{P(I)}}=\displaystyle{\frac{0.42}{0.50}}=0.84 \Rightarrow\)
\(\Rightarrow\) El \(84\%\) de los alumnos que han aprobado Inglés, aprueban también Historia.
-
Para ver si los sucesos \(H\) y \(I\) son independientes, comprobamos si
\(P(H \cap I)=P(H) \cdot P(I)\)
\(\left.\begin{array}{c} P(H) \cdot P(I)=0.60 \cdot 0.50=0.30\\ P(H \cap I)=0.42\\ \end{array}\right\} \Rightarrow\)
\(\Rightarrow\) Los sucesos \(H\) y \(I\) son dependientes.
Dependiendo de lo que nos preguntan en cada problema y de los datos que nos proporcionan, nos interesará más resolverlo mediante una tabla de contingencia o mediante un diagrama de árbol. En este problema en concreto, para rellenar las probabilidades del diagrama de árbol necesitamos hacer uso del Teorema de la Probabilidad Total, mientras que para rellenar las probabilidades de la tabla de contingencia, necesitamos hacer uso de la probabilidad de la intersección.
Resolución mediante diagrama de árbol:
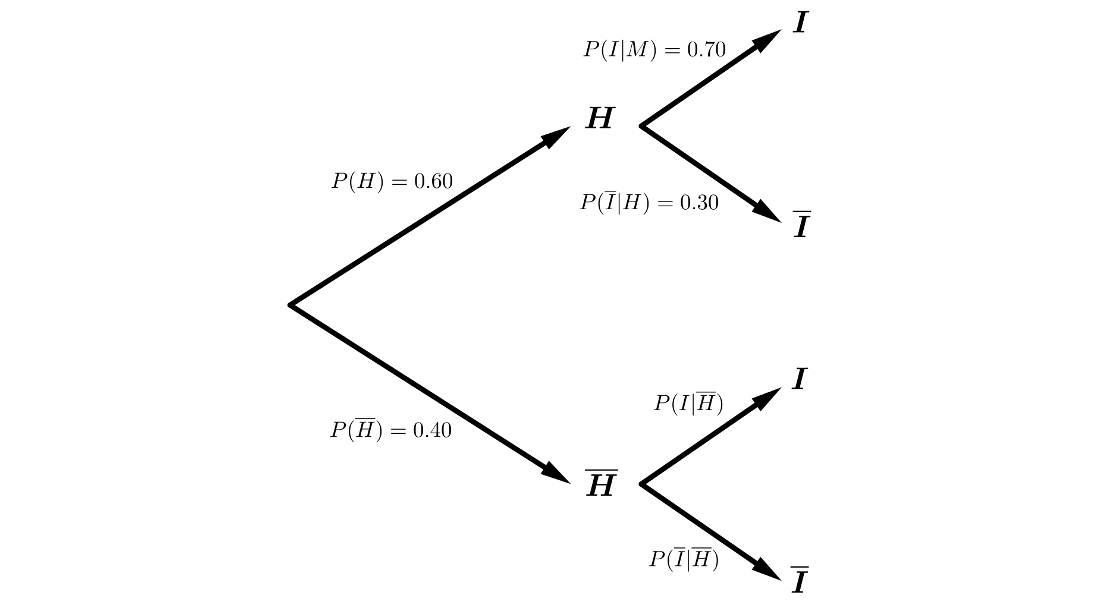
Estamos en un sistema completo de sucesos, por lo que, aplicando el Teorema de la Probabilidad Total:
\(P(I)=P(H \cap I) + P(\overline{H} \cap I) =\)
\(= P(H) \cdot P(I|H)+P(\overline{H}) \cdot P(I|\overline{H}) \Rightarrow\)
\(\Rightarrow 0.75=0.60 \cdot 0.70 + 0.40 \cdot P(I|\overline{H}) \Rightarrow\)
\(\Rightarrow P(I|\overline{H}) = \displaystyle{\frac{0.50 - 0.60 \cdot 0.70}{0.40}}=\displaystyle{\frac{0.08}{0.40}}=0.2\)
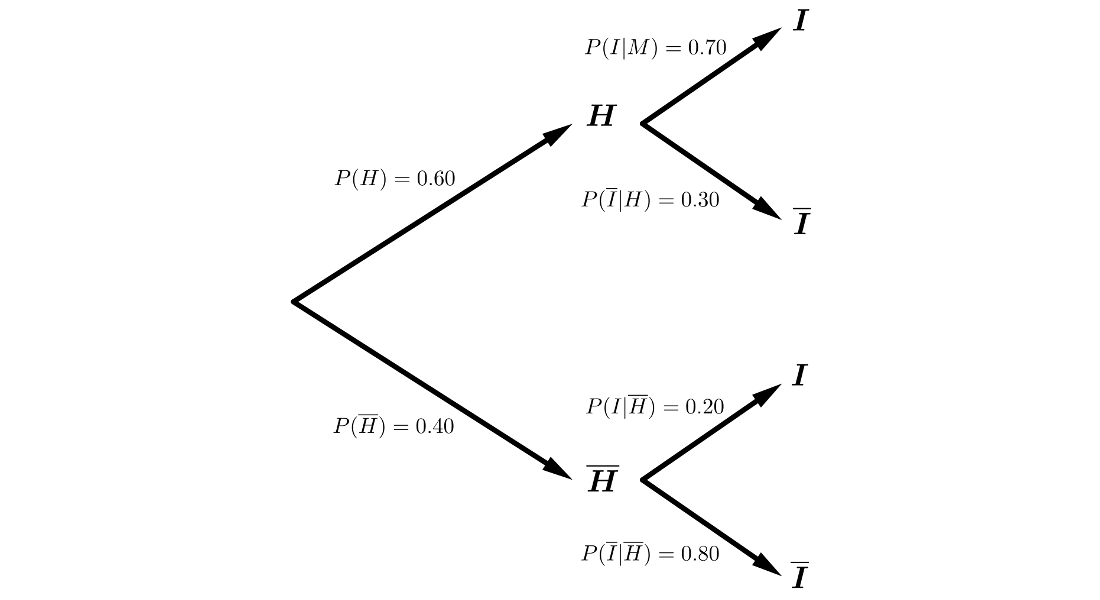
Resolución mediante tabla de contingencia:
Los datos conocidos de la tabla son los sombreados. Los restantes se obtienen a partir de los otros.
| \(\) | \(I\) | \(\overline{I}\) | \(Total\) |
|---|---|---|---|
| \(H\) | \(0.42\) | \(0.18\) | \(0.60\) |
| \(\overline{H}\) | \(0.08\) | \(0.32\) | \(0.40\) |
| \(Total\) | \(0.50\) | \(0.50\) | \(1\) |
Problema (#21)
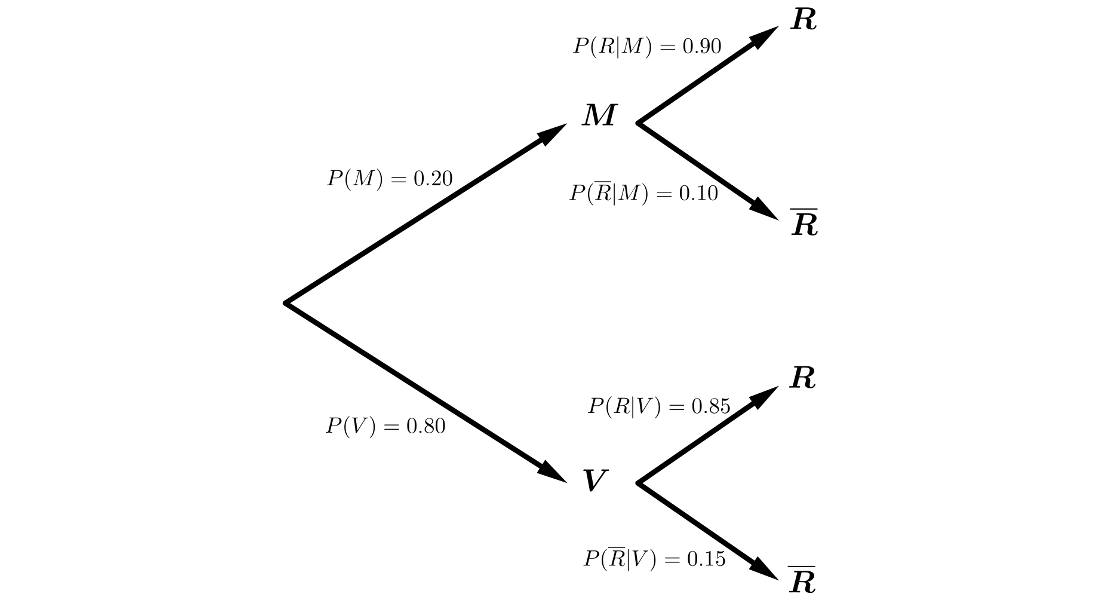
Una compañía aseguradora realiza operaciones de seguros médicos y de seguros de vida. El \(20\%\) de las operaciones corresponde a seguros médicos y el resto a seguros de vida. El porcentaje de operaciones en las que no se producen retrasos en los pagos es del \(10\%\) en los seguros médicos y del \(15\%\) en seguros de vida.
- Halle el porcentaje de operaciones en las que no se producen retrasos en los pagos.
- De las operaciones que han sufrido retrasos en los pagos, ¿qué porcentaje corresponde a los seguros de vida?
Solución:
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
-
Aplicando el Teorema de la Probabilidad Total:
\(P(\overline{R})=P(M \cap \overline{R}) + P(V \cap \overline{R}) =\)
\(=P(M) \cdot P(\overline{R}|M)+P(V) \cdot P(\overline{R}|V)=\)
\(=0.20 \cdot 0.10 + 0.80 \cdot 0.15 = 0.14 \Rightarrow\)
\(\Rightarrow\) En el \(14\%\) de las operaciones no se producen retrasos en los pagos.
-
Aplicando el Teorema de Bayes:
\(P(V|R)=\displaystyle{\frac{P(V \cap R)}{P(R)}}=\)
\(=\displaystyle{\frac{P(V) \cdot P(R|V)}{P(M) \cdot P(R|M)+P(V) \cdot P(R|V)}}=\)
\(=\displaystyle{\frac{0.80 \cdot 0.85}{0.20 \cdot 0.90 + 0.80 \cdot 0.85}}=\displaystyle{\frac{0.68}{0.86}}=0.79\)
El \(79\%\) de las operaciones que han sufrido retrasos en los pagos, se corresponde a los seguros de vida.
Obtenemos la \(P(R)\) aplicando el Teorema de la Probabilidad Total:
\(P(R)=P(M \cap R) + P(V \cap R) =\)
\(=P(M) \cdot P(R|M)+P(V) \cdot P(R|V)=\)
\(=0.20 \cdot 0.90 + 0.80 \cdot 0.85 = 0.86\)
También podemos obtener la \(P(R)\) aplicando la probabilidad del contrario:
\(P(R)=1-P(\overline{R})=1-0.14=0.86\)
Problema (#22)
Una bolsa contiene 5 bolas blancas, 3 rojas y 4 negras. Ana y Manolo practican el siguiente juego: Ana saca una bola, anota su color y la devuelve a la bolsa, a continuación Manolo extrae una bola y anota su color. Si las dos bolas extraídas tienen el mismo color gana Ana, si sólo hay una bola blanca gana Manolo, y en otro caso hay empate.
- Calcule la probabilidad de que gane Ana.
- Calcule la probabilidad de que gane Manolo.
- Calcule la probabilidad de que haya empate.
Solución:
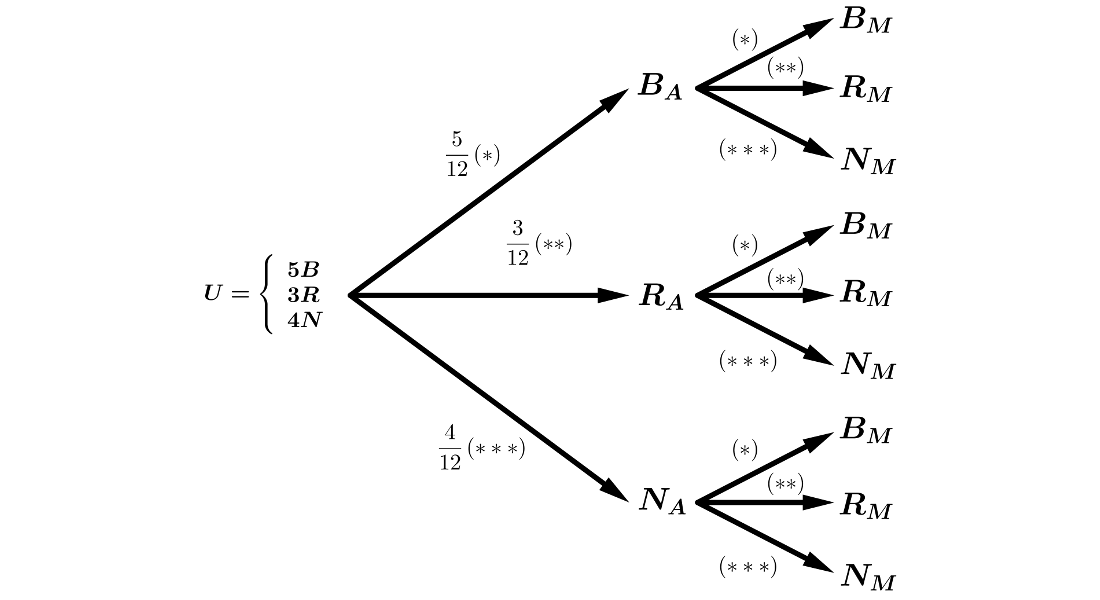
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
Consideremos los sucesos \(G_A=\)"Gana Ana", \(G_M=\)"Gana Manolo" y \(E=\)"Se produce un empate".
-
Aplicando el Teorema de la Probabilidad Total:
\(P(G_A)=P(B_A \cap B_M) + P(R_A \cap R_M) + P(N_A \cap N_M) = \)
\(= P(B_A) \cdot P(B_M|B_A) + P(R_A) \cdot P(R_M|R_A) + P(N_A) \cdot P(N_M|N_A) =\)
\(=\displaystyle{\frac{5}{12}} \cdot \displaystyle{\frac{5}{12}} + \displaystyle{\frac{3}{12}} \cdot \displaystyle{\frac{3}{12}} + \displaystyle{\frac{4}{12}} \cdot \displaystyle{\frac{4}{12}} =\)
\(=\displaystyle{\frac{25}{144}} + \displaystyle{\frac{9}{144}} + \displaystyle{\frac{16}{144}} = \displaystyle{\frac{50}{144}} = \displaystyle{\frac{25}{72}} = 0.35\)
-
Aplicando el Teorema de la Probabilidad Total:
\(P(G_M)=P(B_A \cap R_M) + P(B_A \cap R_M) + P(R_A \cap B_M) + P(N_A \cap B_M) =\)
\(=P(B_A) \cdot P(R_M|B_A) + P(B_A) \cdot P(R_M|B_A) + P(R_A) \cdot P(B_M|R_A) + P(N_A) \cdot P(N_M|N_A) =\)
\(=\displaystyle{\frac{5}{12}} \cdot \displaystyle{\frac{3}{12}} + \displaystyle{\frac{5}{12}} \cdot \displaystyle{\frac{4}{12}} + \displaystyle{\frac{3}{12}} \cdot \displaystyle{\frac{5}{12}} + \displaystyle{\frac{4}{12}} \cdot \displaystyle{\frac{5}{12}} =\)
\(=\displaystyle{\frac{15}{144}} + \displaystyle{\frac{20}{144}} + \displaystyle{\frac{15}{144}} + \displaystyle{\frac{20}{144}} = \displaystyle{\frac{70}{144}} = \displaystyle{\frac{35}{72}} = 0.49\)
-
Aplicando el Teorema de la Probabilidad Total:
\(P(E)=P(R_A \cap N_M) + P(N_A \cap R_M) =\)
\(= P(R_A) \cdot P(N_M|R_A) + P(N_A) \cdot P(R_M|N_A) =\)
\(=\displaystyle{\frac{3}{12}} \cdot \displaystyle{\frac{4}{12}} + \displaystyle{\frac{4}{12}} \cdot \displaystyle{\frac{3}{12}} = \displaystyle{\frac{12}{144}} + \displaystyle{\frac{12}{144}} =\)
\(=\displaystyle{\frac{24}{144}} = \displaystyle{\frac{1}{6}} = 0.17\)
También podemos obtener la \(P(E)\) aplicando la probabilidad del contrario:
\(E=\)"Se produce un empate" = "No gane Ana ni Manolo"
Aplicando las leyes de Morgan:
\(P(E)=P(\overline{G_A} \cap \overline{G_M})=P(\overline{G_A \cup G_M})=\)
\(=1-P(G_A \cup G_M)=1-0.84=0.16\)
\(P(G_A \cap G_M)=0\) al ser \(G_A\) y \(G_M\) sucesos incompatibles.
Por tanto, aplicando la probabilidad de la unión:
\(P(G_A \cup G_M)=P(G_A)+P(G_M)-P(G_A \cap G_M)=\)
\(=0.35+0.49-0=0.84\)
Problema (#23)
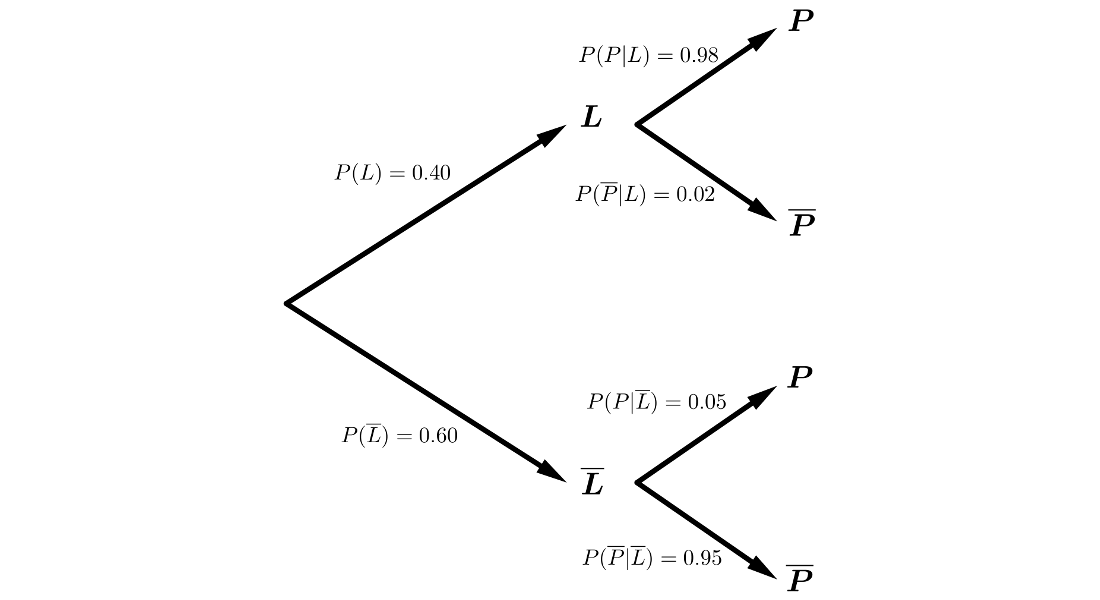
Pedro vive en una ciudad donde el \(40\%\) de los días del año hay riesgo de lluvia y el resto no lo hay. Cuando hay riesgo de lluvia, Pedro coge el paraguas un \(98\%\) de las veces y cuando no lo hay, un \(5\%\) de las veces. Si se selecciona un día del año al azar:
- ¿Cuál es la probabilidad de que Pedro no haya cogido el paraguas ese día?
- ¿Cuál es la probabilidad de que exista riesgo de lluvia, si sabemos que ese día Pedro ha cogido el paraguas?
Solución:
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
-
Aplicando el Teorema de la Probabilidad Total:
\(P(\overline{P})=P(L \cap \overline{P}) + P(\overline{L} \cap \overline{P}) =\)
\(=P(L) \cdot P(\overline{P}|L)+P(\overline{L}) \cdot P(\overline{P}|\overline{L})=\)
\(=0.40 \cdot 0.02 + 0.60 \cdot 0.95 = 0.58\)
-
Aplicando el Teorema de Bayes:
\(P(L|P)=\displaystyle{\frac{P(L \cap P)}{P(P)}}=\)
\(=\displaystyle{\frac{P(L) \cdot P(P|L)}{P(L) \cdot P(P|L)+P(\overline{L}) \cdot P(P|\overline{L})}}=\)
\(=\displaystyle{\frac{0.40 \cdot 0.98}{0.40 \cdot 0.98 + 0.60 \cdot 0.05}}=\displaystyle{\frac{0.39}{0.42}}=0.16\)
Obtenemos la \(P(R)\) aplicando el Teorema de la Probabilidad Total:
\(P(P)=P(L \cap P) + P(\overline{L} \cap P) =\)
\(= P(L) \cdot P(P|L)+P(\overline{L}) \cdot P(P|\overline{L})=\)
\(=0.40 \cdot 0.98 + 0.60 \cdot 0.05 = 0.42\)
También podemos obtener la \(P(R)\) aplicando la probabilidad del contrario:
\(P(P)=1-P(\overline{P})=1-0.58=0.42\)
Problema (#24)
Un jugador lanza a la vez un dado y una moneda.
- Construya el espacio muestral de este experimento aleatorio.
- Determine la probabilidad del suceso A: “El jugador obtiene un número par en el dado y cruz en la moneda”.
- Si sabemos que en la moneda ha salido cara, ¿cuál es la probabilidad de que en el dado haya salido más de 3 puntos?
Solución:
-
\(E=\displaystyle{\left\{1c,1x,2c,2x,3c,3x,4c,4x,5c,5x,6c,6x\right\}}\)
-
\(A=\displaystyle{\left\{2x,4x,6x\right\}}\)
Aplicando la regla de Laplace: \(P(A)=\displaystyle{\frac{3}{12}}=\displaystyle{\frac{1}{4}}=0.25\)
-
\(B=\)"Obtener número mayor que 3"\(=\displaystyle{\left\{4c,4x,5c,5x,6c,6x\right\}}\)
Aplicando la regla de Laplace: \(P(B)=\displaystyle{\frac{6}{12}}=\displaystyle{\frac{1}{2}}=0.50\)
\(C=\)"Obtener cara"\(=\displaystyle{\left\{1c,2c,3c,4c,5c,6c\right\}}\)
Aplicando la regla de Laplace: \(P(C)=\displaystyle{\frac{6}{12}}=\displaystyle{\frac{1}{2}}=0.50\)
\(B \cap C=\displaystyle{\left\{4c,5c,6c\right\}}\)
Aplicando la regla de Laplace: \(P(B \cap C)=\displaystyle{\frac{3}{12}}=\displaystyle{\frac{1}{4}}=0.25\)
Aplicando la definición de probabilidad condicionada:
\(P(B|C)=\displaystyle{\frac{P(B \cap C)}{P(C)}}=\displaystyle{\frac{0.25}{0.50}}=0.50\)
Problema (#25)
Un libro tiene cuatro capítulos. El primer capítulo tiene \(140\) páginas, el segundo \(100\), el tercero \(150\) y el cuarto \(50\). El \(5\%\) de las páginas del primer capítulo, el \(4\%\) del segundo y el \(2\%\) del tercero tienen algún error. Las páginas del cuarto capítulo no tienen errores.
- ¿Cuál es la probabilidad de que, al elegir una página al azar, tenga algún error?
- Supongamos que elegimos una página al azar y observamos que no tiene ningún error, ¿cuál es la probabilidad de que sea del segundo capítulo?
Solución:
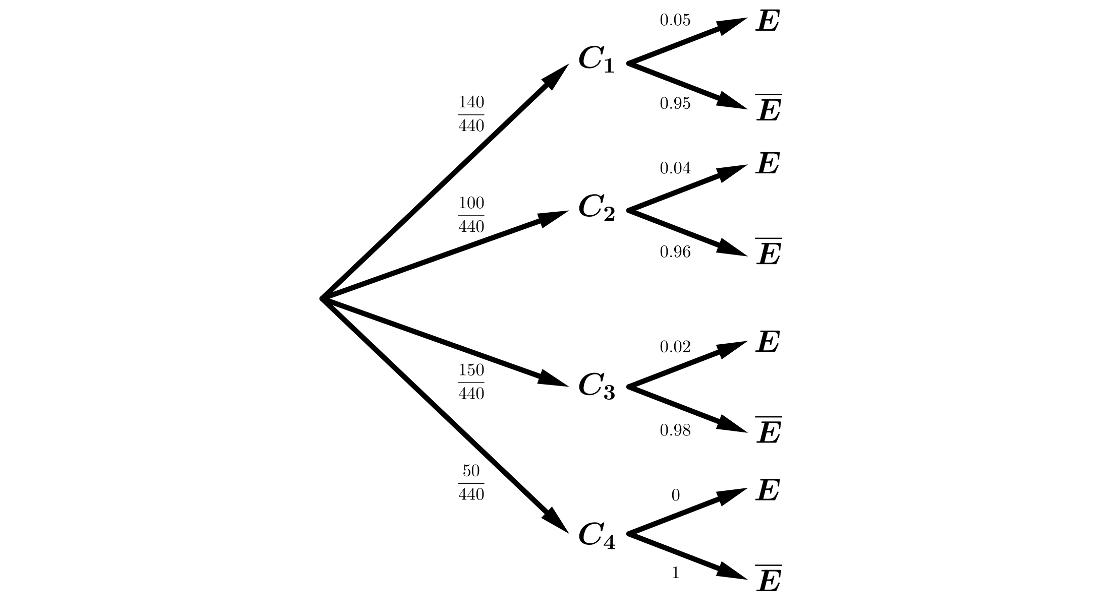
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
-
Aplicando el Teorema de la Probabilidad Total:
\(P(E)=P(C_1 \cap E) + P(C_2 \cap E) + P(C_3 \cap E) + P(C_4 \cap E) = \)
\(=P(C_1) \cdot P(E|C_1)+P(C_2) \cdot P(E|C_2)+P(C_3) \cdot P(E|C_3)+P(C_4) \cdot P(E|C_4)=\)
\(=\displaystyle{\frac{140}{440}} \cdot 0.05 + \displaystyle{\frac{100}{440}} \cdot 0.04 + \displaystyle{\frac{150}{440}} \cdot 0.02 + \displaystyle{\frac{50}{440}} \cdot 0 = 0.03\)
-
Aplicando el Teorema de Bayes:
\(P(C_2|\overline{E})=\displaystyle{\frac{P(C_2 \cap \overline{E})}{P(\overline{E})}}=\)
\(=\displaystyle{\frac{P(C_2) \cdot P(\overline{E}|C_2)}{P(C_1) \cdot P(\overline{E}|C_1)+P(C_2) \cdot P(\overline{E}|C_2)+P(C_3) \cdot P(\overline{E}|C_3)+P(C_4) \cdot P(\overline{E}|C_4)}}=\)
\(=\displaystyle{\frac{\displaystyle{\frac{100}{440}} \cdot 0.96}{\displaystyle{\frac{140}{440}} \cdot 0.95 + \displaystyle{\frac{100}{440}} \cdot 0.96 + \displaystyle{\frac{150}{440}} \cdot 0.98 + \displaystyle{\frac{50}{440}} \cdot 1}}=\)
\(=\displaystyle{\frac{0.22}{0.97}}= 0.23\)
Obtenemos la \(P(B_2)\) aplicando el Teorema de la Probabilidad Total:
\(P(\overline{E})=P(C_1) \cdot P(\overline{E}|C_1)+P(C_2) \cdot P(\overline{E}|C_2)+P(C_3) \cdot P(\overline{E}|C_3)+P(C_4) \cdot P(\overline{E}|C_4) =\)
\(=\displaystyle{\frac{140}{440}} \cdot 0.95 + \displaystyle{\frac{100}{440}} \cdot 0.96 + \displaystyle{\frac{150}{440}} \cdot 0.98 + \displaystyle{\frac{50}{440}} \cdot 1 = 0.97\)
También podemos obtener la \(P(\overline{E})\) aplicando la probabilidad del contrario:
\(P(\overline{E})=1-P(E)=1-0.03=0.97\)
Problema (#26)
La probabilidad de que un jugador A marque un gol de penalti es de \(\displaystyle{\frac{5}{6}}\), mientras que la de otro jugador B es \(\displaystyle{\frac{4}{5}}\). Si cada uno lanza un penalti,
- Halle la probabilidad de que marque gol uno solo de los dos jugadores.
- Halle la probabilidad de que al menos uno marque gol.
Solución:
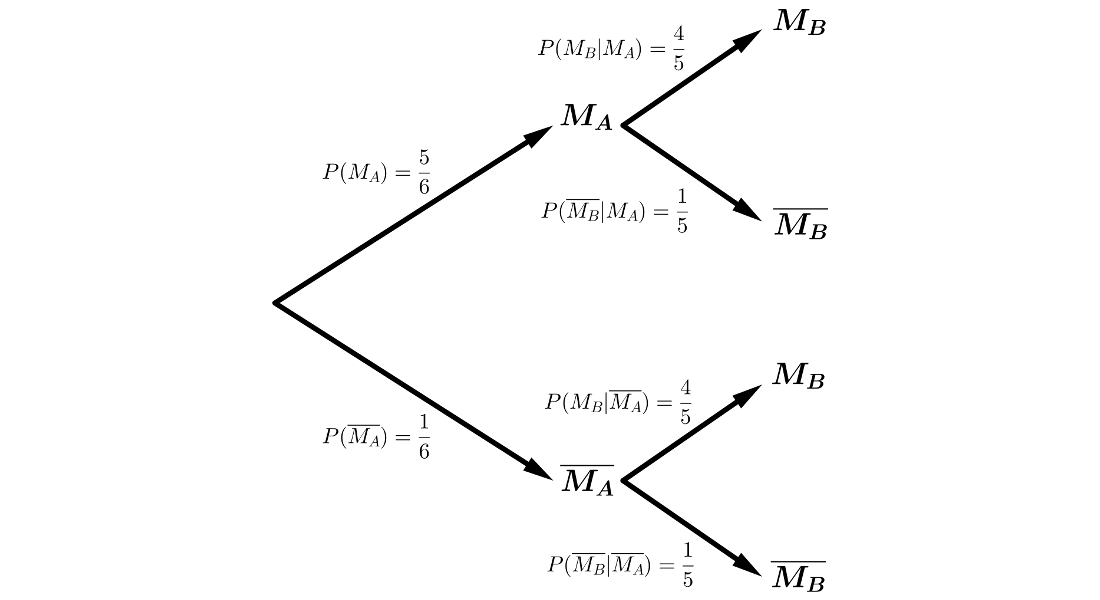
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
-
Consideremos el suceso \(C=\) "Marque gol uno solo de los dos jugadores"
Aplicando el Teorema de la Probabilidad Total:
\(P(C)=P(M_A \cap \overline{M_B}) + P(\overline{M_A} \cap M_B) =\)
\(=P(M_A) \cdot P(\overline{M_B}|M_A)+P(\overline{M_A}) \cdot P(M_B|\overline{M_A})=\)
\(=\displaystyle{\frac{5}{6}} \cdot \displaystyle{\frac{1}{5}} + \displaystyle{\frac{1}{6}} \cdot \displaystyle{\frac{4}{5}} = \displaystyle{\frac{9}{30}}=\displaystyle{\frac{3}{10}}=0.30\)
-
Consideremos el suceso \(D=\) "Al menos uno marque gol" y \(\overline{D}=\) "Ninguno de los dos marque gol"
Aplicando la probabilidad de la intersección:
\(P(\overline{D})=P(\overline{M_A} \cap \overline{M_B})=P(\overline{M_A}) \cdot P(\overline{M_B}|\overline{M_A})=\)
\(=\displaystyle{\frac{1}{6}} \cdot \displaystyle{\frac{1}{5}}=\displaystyle{\frac{1}{30}}=0.03\)
Obtenemos la \(P(D)\) aplicando la probabilidad del contrario:
\(P(D)=1-P(\overline{D})=1-\displaystyle{\frac{1}{30}}=\displaystyle{\frac{29}{30}}=0.97\)
También podríamos obtener \(P(D)\) aplicando el Teorema de la Probabilidad Total:
\(P(D)=P(M_A \cap M_B)+P(M_A \cap \overline{M_B})+P(\overline{M_A} \cap M_B)=\)
\(=P(M_A) \cdot P(M_B|M_A)+P(M_A) \cdot P(\overline{M_B}|M_A)+P(\overline{M_A}) \cdot P(M_B|\overline{M_A})=\)
\(=\displaystyle{\frac{5}{6}} \cdot \displaystyle{\frac{4}{5}}+\displaystyle{\frac{5}{6}} \cdot \displaystyle{\frac{1}{5}}+\displaystyle{\frac{1}{6}} \cdot \displaystyle{\frac{4}{5}}=\)
\(=\displaystyle{\frac{4}{6}}+\displaystyle{\frac{1}{6}}+\displaystyle{\frac{4}{30}}=\displaystyle{\frac{29}{30}}=0.97\)
Problema (#27)
Una caja contiene diez tornillos, de los que dos son defectuosos.
- Si vamos extrayendo tornillos, uno tras otro, hasta localizar los dos defectuosos, ¿cuál es la probabilidad de necesitar exactamente tres extracciones para localizarlos?
- Si extraemos sólo dos tornillos, y el segundo ha resultado ser defectuoso, ¿cuál es la probabilidad de que el primero también lo haya sido?
Solución:
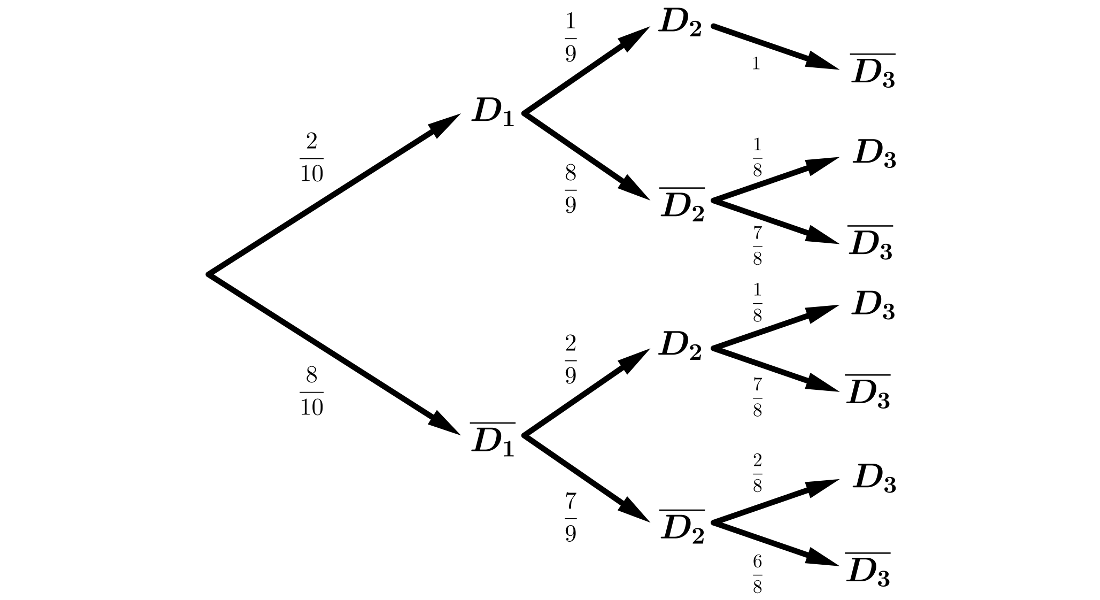
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
-
Consideremos los sucesos \(T=\)"Necesitar exactamente tres extracciones para localizarlos" y \(\overline{T}=\)"Necesitar menos de tres extracciones para localizarlos".
Aplicando el Teorema de la Probabilidad Total:
\(P(T)=P(D_1 \cap \overline{D_2} \cap D_3) + P(\overline{D_1} \cap D_2 \cap D_3) = \)
\(= P(D_1) \cdot P(\overline{D_2}|D_1) \cdot P(D_3|D_1 \cap \overline{D_2}) + P(\overline{D_1}) \cdot P(D_2|\overline{D_1}) \cdot P(D_3|\overline{D_1} \cap D_2) = \)
\(=\displaystyle{\frac{2}{10}} \cdot \displaystyle{\frac{1}{9}} \cdot \displaystyle{\frac{1}{8}} + \displaystyle{\frac{8}{10}} \cdot \displaystyle{\frac{2}{9}} \cdot \displaystyle{\frac{1}{8}} = \displaystyle{\frac{2}{90}} + \displaystyle{\frac{2}{90}} =\)
\(=\displaystyle{\frac{4}{90}} = \displaystyle{\frac{2}{45}} = 0.04\)
-
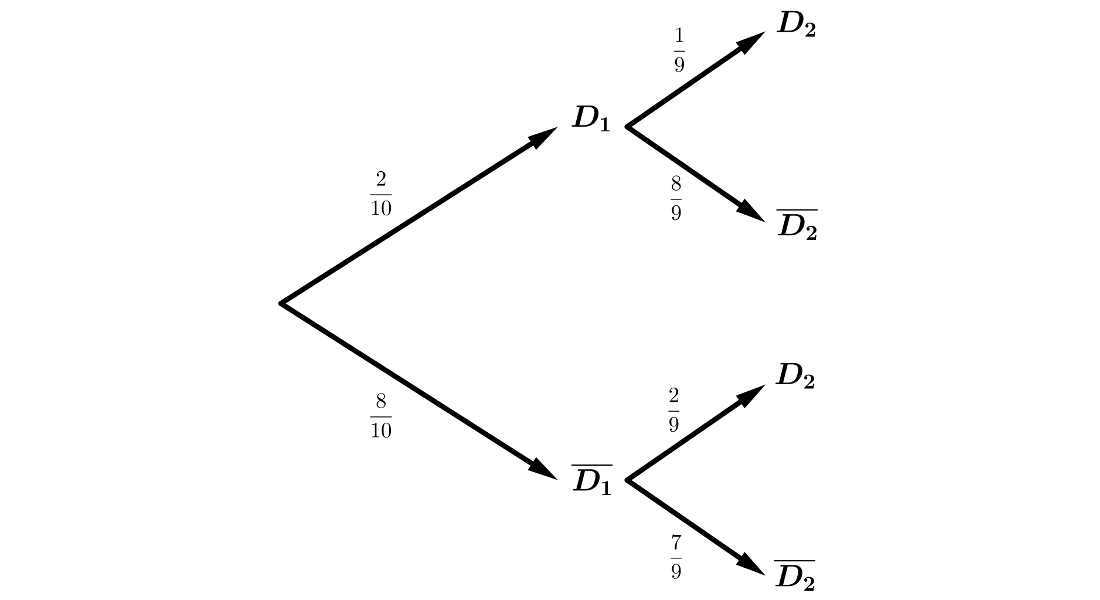
Aplicando el Teorema de Bayes:
\(P(D_1|D_2)=\displaystyle{\frac{P(D_1 \cap D_2)}{P(D_2)}}=\)
\(=\displaystyle{\frac{P(D_1) \cdot P(D_2|D_1)}{P(D_1) \cdot P(D_2|D_1)+P(\overline{D_1}) \cdot P(D_2|\overline{D_1})}}=\)
\(=\displaystyle{\frac{\displaystyle{\frac{2}{10}} \cdot \displaystyle{\frac{1}{9}}}{\displaystyle{\frac{2}{10}} \cdot \displaystyle{\frac{1}{9}} + \displaystyle{\frac{8}{10}} \cdot \displaystyle{\frac{2}{9}}}}=\displaystyle{\frac{\displaystyle{\frac{2}{90}}}{\displaystyle{\frac{18}{90}}}}=\)
\(=\displaystyle{\frac{2}{18}} =\displaystyle{\frac{1}{9}} = 0.11\)
Obtenemos la \(P(D_2)\) aplicando el Teorema de la Probabilidad Total:
\(P(D_2)=P(D_1 \cap D_2) + P(\overline{D_1} \cap D_2) =\)
\(= P(D_1) \cdot P(D_2|D_1)+P(\overline{D_1}) \cdot P(D_2|\overline{D_1}) = \)
\(=\displaystyle{\frac{2}{10}} \cdot \displaystyle{\frac{1}{9}} + \displaystyle{\frac{8}{10}} \cdot \displaystyle{\frac{2}{9}} = \displaystyle{\frac{18}{90}} = \displaystyle{\frac{1}{5}} = 0.20\)
Problema (#28)
Un examen consta de una parte teórica y una parte práctica. La probabilidad de que se apruebe la parte teórica es \(0.7\) y la de que se apruebe la parte práctica \(0.75\). Se sabe que el \(50\%\) de los alumnos ha aprobado ambas.
- Calcule la probabilidad de aprobar alguna de las dos partes.
- Calcule la probabilidad de aprobar la parte práctica sabiendo que no se ha aprobado la parte teórica.
- ¿Son independientes los sucesos “aprobar parte teórica” y “aprobar parte práctica”?
Solución:
| \(\) | \(P\) | \(\overline{P}\) | \(Total\) |
|---|---|---|---|
| \(T\) | \(0.50\) | \(0.20\) | \(0.70\) |
| \(\overline{T}\) | \(0.25\) | \(0.05\) | \(0.30\) |
| \(Total\) | \(0.75\) | \(0.25\) | \(1\) |
-
Aplicando la probabilidad de la unión:
\(P(T \cup P)=P(T)+P(P)-P(T \cap P)=\)
\(=0.70+0.75-0.50=0.95 \Rightarrow\)
\(\Rightarrow P(T \cup P)=0.95\)
-
Aplicando la definición de probabilidad condicionada:
\(P(P|\overline{T})=\displaystyle{\frac{P(P \cap \overline{T})}{P(\overline{T})}}=\displaystyle{\frac{0.25}{0.30}}=0.83\)
-
Para ver si los sucesos \(T\) y \(P\) son independientes, comprobamos si
\(P(T \cap P)=P(T) \cdot P(P)\)
\(\left.\begin{array}{c} P(T) \cdot P(P)=0.70 \cdot 0.75=0.53\\ P(T \cap P)=0.50\\ \end{array}\right\} \Rightarrow\)
\(\Rightarrow\) Los sucesos \(T\) y \(P\) son dependientes.
Problema (#29)
En un sistema de alarma, la probabilidad de que haya un incidente es \(0,1\). Si éste se produce, la probabilidad de que la alarma suene es \(0,95\). La probabilidad de que suene la alarma sin que haya incidente es de \(0,03\).
- ¿Cuál es la probabilidad de que suene la alarma?
- Si ha sonado la alarma, calcule la probabilidad de que no haya habido incidente.
Solución:
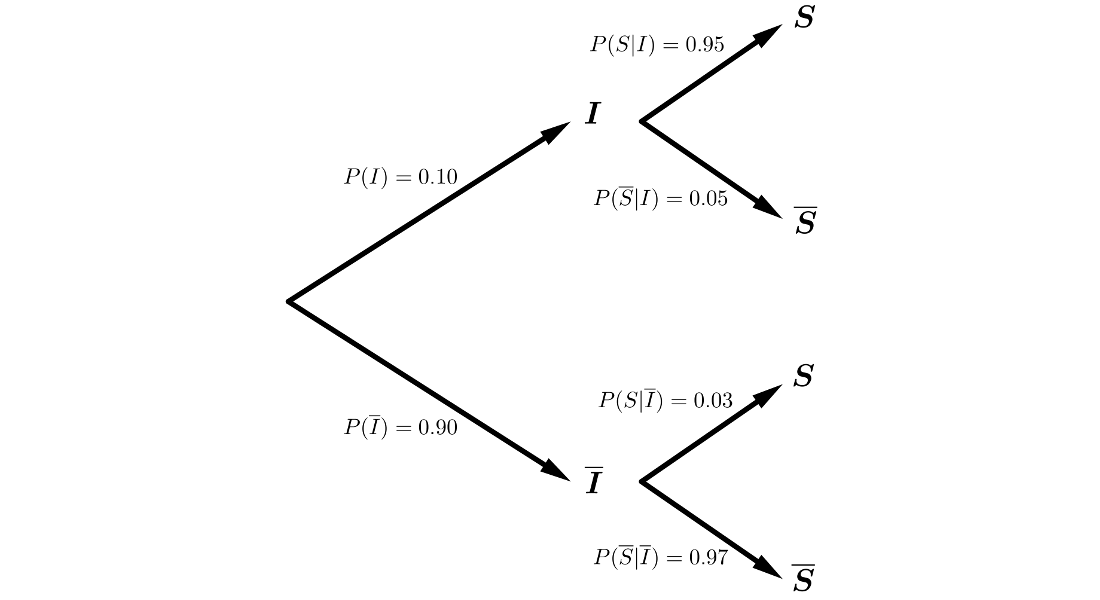
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
-
Aplicando el Teorema de la Probabilidad Total:
\(P(S)=P(I \cap S) + P(\overline{I} \cap S) =\)
\(= P(I) \cdot P(S|I)+P(\overline{I}) \cdot P(S|\overline{I})=\)
\(=0.10 \cdot 0.95 + 0.90 \cdot 0.03 = 0.12\)
-
Aplicando el Teorema de Bayes:
\(P(\overline{I}|S)=\displaystyle{\frac{P(\overline{I} \cap S)}{P(S)}}=\)
\(=\displaystyle{\frac{P(\overline{I}) \cdot P(S|\overline{I})}{P(I) \cdot P(S|I)+P(\overline{I}) \cdot P(S|\overline{I})}}=\)
\(=\displaystyle{\frac{0.90 \cdot 0.03}{0.10 \cdot 0.95 + 0.90 \cdot 0.03}}=\)
\(=\displaystyle{\frac{0.027}{0.12}}=0.23\)
Problema (#30)
En una ciudad, el \(55\%\) de la población consume aceite de oliva, el \(30\%\) de girasol, y el \(20\%\) ambos tipos. Se escoge una persona al azar:
- Si consume aceite de oliva, ¿cuál es la probabilidad de que consuma también aceite de girasol?
- Si consume aceite de girasol, ¿cuál es la probabilidad de que no consuma aceite de oliva?
- ¿Cuál es la probabilidad de que no consuma ninguno de los dos tipos de aceite?
Solución:
| \(\) | \(G\) | \(\overline{G}\) | \(Total\) |
|---|---|---|---|
| \(O\) | \(0.20\) | \(0.35\) | \(0.55\) |
| \(\overline{O}\) | \(0.10\) | \(0.35\) | \(0.45\) |
| \(Total\) | \(0.30\) | \(0.70\) | \(1\) |
-
Aplicando la definición de probabilidad condicionada:
\(P(G|O)=\displaystyle{\frac{P(G \cap O)}{P(O)}}=\displaystyle{\frac{0.20}{0.55}}=0.36\)
-
Aplicando la definición de probabilidad condicionada:
\(P(\overline{O}|G)=\displaystyle{\frac{P(\overline{O} \cap G)}{P(G)}}=\displaystyle{\frac{0.10}{0.30}}=0.33\)
- \(P(\overline{O} \cap \overline{G})=0.35\)
Problema (#31)
El \(30\%\) de los aparatos que llegan a un servicio técnico para ser reparados están en garantía. De los que no están en garantía, el \(20\%\) ya fueron reparados en otra ocasión y de los que sí lo están, solamente un \(5\%\) fueron reparados anteriormente. Se elige un aparato al azar en el servicio técnico:
- ¿Cuál es la probabilidad de que haya sido reparado en otra ocasión?
- Si es la primera vez que ha llegado al servicio técnico, ¿cuál es la probabilidad de que esté en garantía?
Solución:
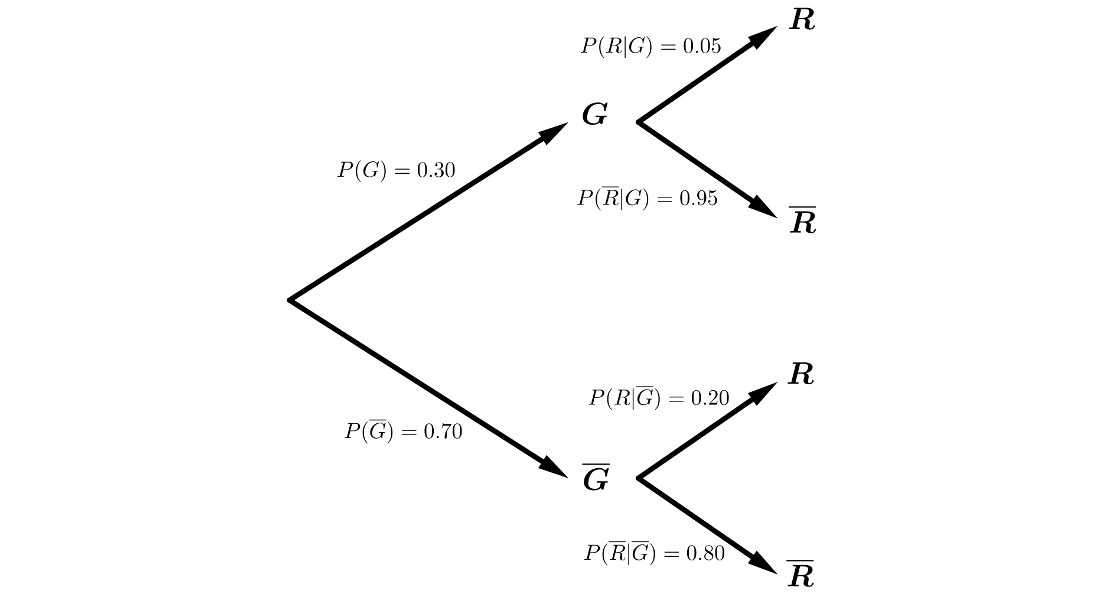
Estamos en un sistema completo de sucesos, por lo que podemos aplicar los Teoremas de la Probabilidad Total y de Bayes.
-
Aplicando el Teorema de la Probabilidad Total:
\(P(R)=P(G \cap R) + P(\overline{G} \cap R) =\)
\(= P(G) \cdot P(R|G)+P(\overline{G}) \cdot P(R|\overline{G})=\)
\(=0.30 \cdot 0.05 + 0.70 \cdot 0.20 = 0.155\)
-
Aplicando el Teorema de Bayes:
\(P(G|\overline{R})=\displaystyle{\frac{P(G \cap \overline{R})}{P(\overline{R})}}=\)
\(=\displaystyle{\frac{P(G) \cdot P(\overline{R}|G)}{P(G) \cdot P(\overline{R}|G)+P(\overline{G}) \cdot P(\overline{R}|\overline{G})}}=\)
\(=\displaystyle{\frac{0.30 \cdot 0.95}{0.30 \cdot 0.95 + 0.70 \cdot 0.80}}=\)
\(=\displaystyle{\frac{0.285}{0.845}}=0.337\)
Obtenemos la \(P(\overline{R})\) aplicando el Teorema de la Probabilidad Total:
\(P(\overline{R})=P(G \cap \overline{R}) + P(\overline{G} \cap \overline{R}) =\)
\(= P(G) \cdot P(\overline{R}|G)+P(\overline{G}) \cdot P(\overline{R}|\overline{G})=\)
\(=0.30 \cdot 0.95 + 0.70 \cdot 0.80 = 0.845\)
También podemos obtener la \(P(\overline{R})\) aplicando la probabilidad del contrario:
\(P(\overline{R})=1-P(R)=1-0.155=0.845\)
Problema (#32)
En una ciudad el \(60 \%\) de sus habitantes son aficionados al fútbol, el \(30 \%\) son aficionados al baloncesto y el \(25 \%\) a ambos deportes.
- ¿Son independientes los sucesos “ser aficionado al fútbol” y “ser aficionado al baloncesto”?
- Si una persona no es aficionada al fútbol, ¿cuál es la probabilidad de que no sea aficionada al baloncesto?
- Si una persona no es aficionada al baloncesto, ¿cuál es la probabilidad de que sea aficionada al fútbol?
Solución:
Problema (#33)
Dos cajas, \(A\) y \(B\), tienen este contenido:
$$\left\{\begin{array}{ll} A : & \hbox{5 monedas de 1 euro y 3 de 10 pesetas}\\ B : & \hbox{4 monedas de 1 euro, 4 de 10 pesetas y 2 de 25 pesetas}\\ \end{array}\right.$$
De una de las cajas elegida al azar, se extrae una moneda.
- ¿Cuál es la probabilidad de que sea de \(1\) euro?
- Si la moneda extraída resulta ser de \(10\) pesetas, halla la probabilidad de que proceda de la caja \(B\).
Solución:
Problema (#34)
En un cineclub hay \(80\) películas; \(60\) son de “acción” y \(20\) de “terror”. Susana elige una película al azar y se la lleva. A continuación Luis elige otra película al azar.
- ¿Cuál es la probabilidad de que tanto Susana como Luis elijan películas de acción?
- ¿Cuál es la probabilidad de que la película elegida por Luis sea de acción?
Solución:
Problema (#35)
Tenemos un cofre \(A\) con \(2\) monedas de oro y \(3\) de plata, un cofre \(B\) con \(5\) monedas de oro y \(4\) de plata y un tercer cofre \(C\) con \(2\) monedas de oro. Elegimos un cofre al azar y sacamos una moneda.
- Calcule la probabilidad de que sea de oro.
- Sabiendo que ha sido de plata, halle la probabilidad de que haya sido sacada del cofre \(A\).

