Posted by

Zumo de neuronas (#3)


  • Menos
  • EL GOLOSO

    EL GOLOSO: Bill tiene una caja con 2000 caramelos de 5 colores. 387 de ellos son blancos, 396 amarillos, 402 rojos, 407 verdes y 408 marrones. Bill decide comérselos de la siguiente manera: aleatoriamente (sin mirar) saca de la caja 3 caramelos. Si los tres son del mismo color, se los come, en caso contrario los devuelve a la caja. Continúa de esta forma a lo largo del día. Por la noche, cuando Bill tiene un empacho considerable, sólo quedan en la caja dos caramelos del mismo color. ¿De qué color son?

  • LOS SACOS Y LA BALANZA

    LOS SACOS Y LA BALANZA: Tenemos 100 sacos con 100 bolas cada uno. Todas las bolas pesan 10 gramos (cada bola) salvo las que contiene uno de los sacos, en el que todas pesan 9 gramos (cada bola), ¿se puede averiguar cuál es usando una sola vez la balanza?

  • ROMBOS Y TRIÁNGULOS

    ROMBOS Y TRIÁNGULOS: Quita 4 cerillas de las 16 que forman la figura, de manera que queden exactamente 4 triángulos equiláteros iguales.

  • ANTIGUO PROBLEMA ÁRABE: De noche, el palacio Harezhamed lo custodiaban tres guardianes que se situaban en distintos puntos del palacio. Un día, un ladrón llamado Beshain entró y robó un gran saco de cerezas. Al intentar salir de palacio, Beshain fue interceptado por uno de los guardianes. Este le detuvo y le cogió la mitad de las cerezas y cuatro más. Cuando continuó huyendo tropezó con el segundo guardián quien le quitó la mitad de las cerezas que le quedaban y cuatro más. Al final tropezó con el tercer y último guardián quien actúo igual que los otros dos: le quitó la mitad de las cerezas y cuatro más. Si al final se quedó con una sola cereza, ¿cuántas cerezas había robado Beshain?

  • EL ÁREA DEL CUADRADO

    EL ÁREA DEL CUADRADO: Halla el área del cuadrado pequeño central, sabiendo que los cuatro puntos señalados son respectivamente los puntos medios de cada uno de los lados del cuadrado grande. El lado del cuadrado grande mide 5 unidades.

  • CUADRADOS Y RECTÁNGULOS

    CUADRADOS Y RECTÁNGULOS: Un cuadrado se cubre mediante cuatro rectángulos y un cuadrado pequeño. Las dimensiones de cada uno de los lados de los diferentes rectángulos y cuadrados, son números enteros mayores que uno, como se muestra en la figura. Las áreas de dos de dichos rectángulos están escritas sobre ellos. Halla el área del cuadrado pequeño.

  • LAS DOS VELAS Y EL TIEMPO

    LAS DOS VELAS Y EL TIEMPO: Tenemos dos velas exactamente iguales y sabemos que el tiempo que tarda en consumirse cada vela es de 1 hora. Queremos cocer un huevo durante un cuarto de hora exactamente, pero no tenemos reloj. ¿Serías capaz de hacerlo con la única ayuda de las dos velas y un mechero?

  • LA ÚLTIMA CIFRA

    LA ÚLTIMA CIFRA: Suma los cuadrados de los números naturales hasta el 2013 y averigua cuál será su última cifra. No desesperes y usa tu cabeza, será mejor que usar tu calculadora.

  • EL ÁNGULO DESCONOCIDO

    EL ÁNGULO DESCONOCIDO: Sabiendo que los tres lados de mayor longitud de este cuadrilátero tienen una longitud de 1 unidad, ¿serías capaz de obtener el valor del ángulo señalado con el signo de interrogación?

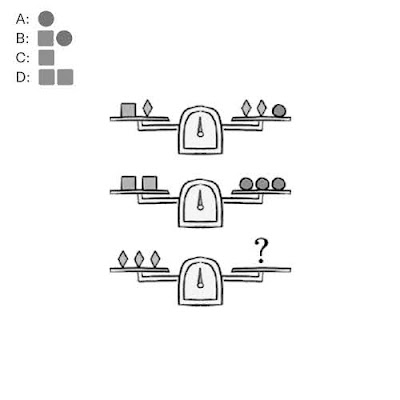
  • LA ECUACIÓN VISUAL

    LA ECUACIÓN VISUAL: Aprovechando que estamos con el tema de ecuaciones y teniendo en cuenta que una ecuación podemos asemejarla a una balanza, ¿sabrías decir qué debemos colocar en el platillo de la derecha de la tercera de las balanzas para que esté equilibrada?

  • Más

En la pestaña OJOS encontrarás las Evidencias de las tareas realizadas con mi alumnado así como sus mejores trabajos. En la pestaña BRAZOS , las Reflexiones sobre mi práctica docente. En la pestaña TENTÁCULOS, una recopilación de materiales para la autoevaluación del alumnado, Formularios útiles para tus clases de Matemáticas, relaciones de Actividades sin resolver (con sus soluciones), Problemas tipo resueltos, Cuestiones teóricas, así como Cuestionarios de Autoevaluación, catalogados por cursos y por unidades didácticas. En la pestaña TINTA, el ARCHIVO completo del blog con todas sus entradas ordenadas cronológicamente. También hay cabida en este sitio para los blogs de aula o portfolios de mis alumn@s en la pestaña CEREBRITOS. Un programa de radio muy particular, Radio Pulpo, en la pestaña EN LA ONDA. En la pestaña POR LA BOCA , podrás encontrar Curiosidades MatemáTICas , y en la pestaña VERDADERO O FALSO, podrás ver Demostraciones MatemáTICas con todo rigor. En la pestaña AMARRAS encontrarás Links interesantes de los que poder tirar. En la pestaña SIN RUMBO dispondrás de Citas célebres que te harán reflexionar. En la pestaña LA PECERA, donde podrás disfrutar de varios Escape Room on line. Por último, en la pestaña EXPRIME TU CEREBRO, una colección de acertijos MatemáTICos para todas las edades.

¿Qué buscas?

ACTIVIDADES AGUJEROS NEGROS NUMÉRICOS ALEATORIO AMORTIZACIÓN ANTERIOR Y POSTERIOR APROXIMACIONES Y ERRORES ÁREAS ARITMÉTICA MERCANTIL AUDIO AUMENTOS Y DESCUENTOS PORCENTUALES
BINGO CALCULADORAS CAPITALIZACIÓN COEDUCACIÓN COMBINATORIA CONSTANTE DE KAPREKAR CONVERTIDORES CONVIVENCIA COORDENADAS POLARES CUADRADO MÁGICO CUADRADOS PERFECTOS CUESTIONARIOS CUESTIONES CURIOSIDADES DEMOSTRACIONES DERIVADAS DÍA DE ANDALUCÍA DÍA DE PI DIAGRAMAS DE VORONOI DISTRIBUCIÓN BERNOULLI DISTRIBUCIÓN BINOMIAL DISTRIBUCIÓN NORMAL ECOacción ECUACIÓN 2ºGRADO ECUACIONES EDICIÓN EDITOR ECUACIONES EDITOR TEXTOS CIENTÍFICOS ENTORNOS ESTADÍSTICA UNIDIMENSIONAL EVIDENCIAS EXTRAER FACTOR COMÚN FACTORIAL FIBONACCI FORMATOS DE TEXTO FÓRMULA DE HERÓN FORMULARIOS FUNCIONES GAMIFICACIÓN GRAFICADORAS GRAMO HOJA DE CÁLCULO HOMBRES I.M.U.S. IDENTIDADES NOTABLES IMAGEN INECUACIONES INTEGRALES INTERÉS COMPUESTO INTERÉS SIMPLE INTERVALOS JERARQUÍA DE OPERACIONES KENKEN LEMNISCATA LEONHARD EULER LINKS LITRO LOGARITMOS LOGICÓN LÚNULA DE HIPÓCRATES MATERIALES EDUCATIVOS MATRICES MÉTODO DE GAUSS METRO METRO CUADRADO METRO CÚBICO MUESTREO E INFERENCIA ESTADÍSTICA MUJERES MULTIPLICACIÓN MULTIPLICACIÓN CON LLEVADA MULTIPLICACIÓN SIN LLEVADA MÚLTIPLOS DEL GRAMO MÚLTIPLOS DEL LITRO MÚLTIPLOS DEL METRO MÚLTIPLOS Y SUBMÚLTIPLOS NOTACIÓN CIENTÍFICA NÚMERO DE ORO NÚMEROS COMPLEJOS NÚMEROS CÓMPLICES NÚMEROS IRRACIONALES NÚMEROS METÁLICOS NÚMEROS RACIONALES NÚMEROS TRIANGULARES PDF PERIODOS DE CAPITALIZACIÓN PEvAU POESÍA POLIEDROS PORCENTAJES POTENCIAS PREMIOS ABEL PREMIOS NOBEL PRIMARIA PROBABILIDAD PROBLEMAS PROGRAMACIÓN LINEAL PROGRESIÓN ARITMÉTICA PROGRESIÓN GEOMÉTRICA PROGRESIÓN RECURSIVA PROGRESIONES PROPORCIÓN DIVINA RACIONALIZAR RADICALES RANGO RECURSOS DE AULA RELOJ ANALÓGICO RELOJ DIGITAL REPRESENTACIÓN DE UNA MULTIPLICACIÓN REPRESENTACIÓN GRÁFICA RESTA CON LLEVADA REVISTAS SECUNDARIA SEGURIDAD EN RED SEMEJANZA SEMIRRECTAS SEXO SIMULACIÓN PROBABILÍSTICA SISTEMA DECIMAL SISTEMA MÉTRICO DECIMAL SISTEMAS DE ECUACIONES LINEALES SISTEMAS DE ECUACIONES NO LINEALES SISTEMAS DE INECUACIONES LINEALES SPINNER SUBMÚLTIPLOS DEL GRAMO SUBMÚLTIPLOS DEL LITRO SUBMÚLTIPLOS DEL METRO SUCESIONES SUDOKU SUMA CON LLEVADA SUMAS Y RESTAS DE MEDIDAS SISTEMA MÉTRICO DECIMAL T.A.E. TABLA BINOMIAL TABLA NORMAL TIPIFICADA TABLAS DE MULTIPLICAR TABLAS DE PROBABILIDAD TEOREMA DE LA ALTURA TEOREMA DE PITÁGORAS TEOREMA DE THALES TEOREMA DE VIVIANI TEOREMA DE ZECKENDORF TEOREMA DEL CATETO TERNAS PITAGÓRICAS TIPIFICAR TRIÁNGULO RECTÁNGULO TRIÁNGULOS TRIÁNGULOS SEMEJANTES VALOR ABSOLUTO VÍDEO
Mostrar más