2ºBACH CCSS REPRESENTACIÓN GRÁFICA DE FUNCIONES (PROBLEMAS)

Representación gráfica de funciones (Aplicaciones de la derivada)

Problema (#1) Representa gráficamente la función $\displaystyle{f(x)=\frac{x^2}{x-1}}$ Solución: Dominio: $$x-1=0 \Leftrightarrow x=+1 \Rightarrow Dom(f)=\mathbb{R} \setminus \left \{+1 \right \}$$ Recorrido: Intercambiamos las variables $x$ e $y$ y despejamos $y$ $$y=\frac{x^2}{x-1} \rightarrow x=\frac{y^2}{y-1} \Rightarrow y=\frac{x \pm \sqrt{x^2 -4x}}{2}$$ $$x^2-4x \geq 0 \Leftrightarrow x \in (-\infty,0] \cup [+4,+\infty) \Rightarrow Rec(f)=(-\infty,0] \cup [+4,+\infty)$$ Puntos de corte con los ejes: $\hbox{ Eje X } (y=0)$ $$\frac{x^2}{x-1}=0 \Leftrightarrow x^2=0 \Leftrightarrow x=0 \Rightarrow O(0,0)$$ $\hbox{ Eje Y } (x=0)$ $$y=\frac{0^2}{0-1} \Leftrightarrow y=0 \Rightarrow O(0,0)$$ Continuidad: La función es continua en $\mathbb{R} \setminus \left \{+1 \right \}$ $x=+1$ Discontinuidad de salto infinito $$\left \{\begin{array}{l} 1) \nexists f(+1)\\ 2) \displaystyle\lim_{x \rightarrow +1} \frac{x^2}{x-1}= \left \{ \begin{matrix} \displaystyle\lim_{x \rightarrow +1^{-}} \frac{x^2}{x-1}=\left[ \frac{1}{0^{-}} \right]=-\infty\\ \displaystyle\lim_{x \rightarrow +1^{+}} \frac{x^2}{x-1}=\left[ \frac{1}{0^{+}} \right]=+\infty\\ \end{matrix} \right.\\ \end{array} \right.$$ Asíntotas: Verticales: $x=+1$ $$\left.\begin{matrix} \displaystyle\lim_{x \rightarrow +1} \frac{x^2}{x^2-1}= \left\{\begin{matrix} \displaystyle\lim_{x \rightarrow +1^{-}} \frac{x^2}{x^2-1}=\left[ \frac{1}{0^{-}} \right]=-\infty\\ \displaystyle\lim_{x \rightarrow +1^{+}} \frac{x^2}{x^2-1}=\left[ \frac{1}{0^{+}} \right]=+\infty\\ \end{matrix} \right.\\ \end{matrix} \right.$$ Horizontales: No tiene asíntotas horizontales $$\left\{ \begin{array}{l} \displaystyle\lim_{x \rightarrow -\infty} \frac{x^2}{x-1}=-\infty\\ \displaystyle\lim_{x \rightarrow +\infty} \frac{x^2}{x-1}=+\infty\\ \end{array} \right.$$ Oblicuas: $y=x+1$ $$\left\{ \begin{array}{l} m = \displaystyle\lim_{x \rightarrow \pm \infty} \frac{\frac{x^2}{x-1}}{x} = \displaystyle\lim_{x \rightarrow \pm \infty} \frac{x^2}{x^2-x} = 1\\ n = \displaystyle\lim_{x \rightarrow \pm \infty} \frac{x^2}{x-1}-1 \cdot x = \displaystyle\lim_{x \rightarrow \pm \infty} \frac{x}{x-1} = 1\\ \end{array} \right.$$ Monotonía y extremos: $f(x)$ es derivable en $\mathbb{R} \setminus \left \{+1 \right \}$ $$f(x)=\frac{x^2}{x-1} \Rightarrow f'(x)=\frac{x^2-2x}{(x-1)^2}$$ Igualamos la derivada primera a cero y resolvemos la ecuación $$f'(x)=\frac{x^2-2x}{(x-1)^2}=0 \Leftrightarrow \frac{x(x-2)}{(x^2-1)^2}=0 \Leftrightarrow \left\{ \begin{matrix} x=0\\ \vee\\ x=+2\\ \end{matrix} \right.$$ $$\left. \begin{array}{l} f'(x) > 0 \hbox{ en } (-\infty,0) \cup (+2,+\infty)\\ f'(x) =0 \hbox{ si } x=+1 \\ f'(x) < 0 \hbox{ en } (0,+1) \cup (+1,+2)\\ \end{array} \right\} \Rightarrow \left. \begin{array}{l} f \nearrow \hbox{ en } (-\infty,0) \cup (+2,+\infty)\\ f \searrow \hbox{ en } (0,+1) \cup (+1,+2)\\ \end{array} \right\} \Rightarrow$$ $$\Rightarrow \left\{ \begin{array}{l} f(x) \hbox{ tiene un máximo relativo en } x=0\\ f(x) \hbox{ tiene un mínimo relativo en } x=+2\\ \end{array} \right.$$ Curvatura y puntos de inflexión: $f'(x)$ es derivable en $\mathbb{R} \setminus \left \{+1 \right \}$ $$f'(x)=\frac{x^2-2x}{(x-1)^2} \Rightarrow f''(x)=\frac{2}{(x-1)^3}$$ Igualamos la derivada segunda a cero y resolvemos la ecuación $$f''(x)=\frac{2}{(x-1)^3}=0 \Leftrightarrow 2=0 \Rightarrow$$ $$\left. \begin{array}{l} f''(x) < 0 \hbox{ en } (-\infty,+1)\\ f''(x) > 0 \hbox{ en } (+1,+\infty)\\ \end{array} \right\} \Rightarrow \left. \begin{array}{l} f \hbox{ cóncava en } (-\infty,+1)\\ f \hbox{ convexa en } (+1,+\infty)\\ \end{array} \right\} \Rightarrow$$ $\Rightarrow f(x)$ no tiene puntos de inflexión Simetría: La función no es simétrica $$f(-x)=\frac{(-x)^2}{(-x)-1}=\frac{x^2}{-x-1} \neq \left\{ \begin{matrix} f(x)\\ \wedge\\ -f(x)\\ \end{matrix} \right.$$ Periodicidad: La función no es periódica Tabla de valores: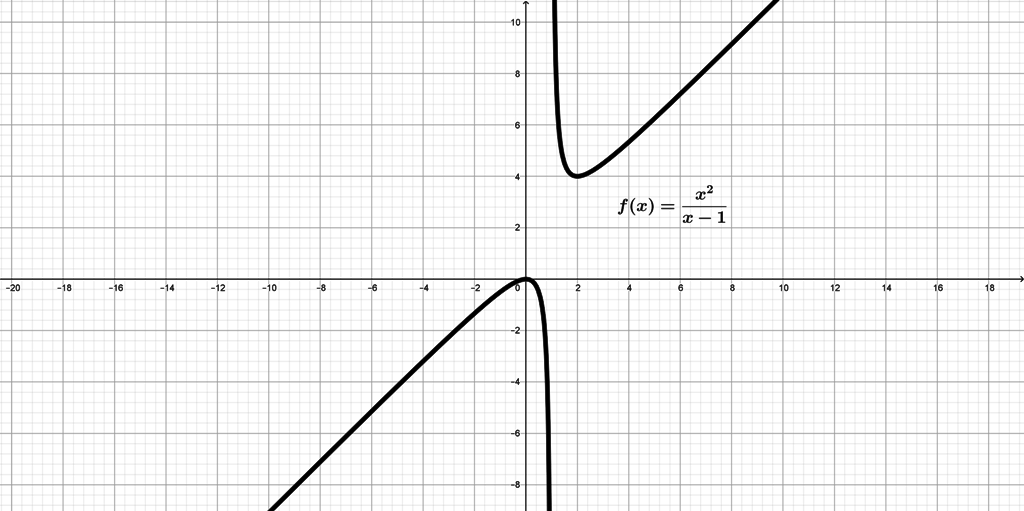

Problema (#2)

Representa gráficamente la función $\displaystyle{f(x)=\frac{x^2}{x^2-1}}$

Solución:

Dominio:

$$x^2-1=0 \Leftrightarrow x=\pm 1 \Rightarrow Dom(f)=\mathbb{R} \setminus \left \{-1,+1 \right \}$$

Recorrido: Intercambiamos las variables $x$ e $y$ y despejamos $y$

$$y=\frac{x^2}{x^2-1} \rightarrow x=\frac{y^2}{y^2-1} \Rightarrow y=\sqrt{\frac{x}{x-1}}$$ $$\frac{x}{x-1} \geq 0 \Leftrightarrow x \in (-\infty,0] \cup (+1,+\infty) \Rightarrow Rec(f)=(-\infty,0] \cup (+1,+\infty)$$

Puntos de corte con los ejes:

$\hbox{ Eje X } (y=0)$

$$\frac{x^2}{x^2-1}=0 \Leftrightarrow x^2=0 \Leftrightarrow x=0 \Rightarrow O(0,0)$$

$\hbox{ Eje Y } (x=0)$

$$y=\frac{0^2}{0^2-1} \Leftrightarrow y=0 \Rightarrow O(0,0)$$

Continuidad: La función es continua en $\mathbb{R} \setminus \left \{-1,+1 \right \}$

$x=-1$ Discontinuidad de salto infinito

$$\left \{\begin{array}{l} (1) \nexists f(-1)\\ (2) \displaystyle\lim_{x \rightarrow -1} \frac{x^2}{x^2-1}= \left \{ \begin{array}{l} \displaystyle\lim_{x \rightarrow -1^{-}} \frac{x^2}{x^2-1}=\left[ \frac{1}{0^{+}} \right]=+\infty\\ \displaystyle\lim_{x \rightarrow -1^{+}} \frac{x^2}{x^2-1}=\left[ \frac{1}{0^{-}} \right]=-\infty\\ \end{array} \right.\\ \end{array} \right.$$

$x=+1$ Discontinuidad de salto infinito

$$\left \{\begin{array}{l} (1) \nexists f(+1)\\ (2) \displaystyle\lim_{x \rightarrow +1} \frac{x^2}{x^2-1}= \left \{ \begin{array}{l} \displaystyle\lim_{x \rightarrow +1^{-}} \frac{x^2}{x^2-1}=\left[ \frac{1}{0^{-}} \right]=-\infty\\ \displaystyle\lim_{x \rightarrow +1^{+}} \frac{x^2}{x^2-1}=\left[ \frac{1}{0^{+}} \right]=+\infty\\ \end{array} \right.\\ \end{array} \right.$$

Asíntotas:

Verticales: $x=-1 \hbox{ y } x=+1$

$$\left\{\begin{array}{l} \displaystyle\lim_{x \rightarrow -1} \frac{x^2}{x^2-1}= \left\{\begin{array}{l} \displaystyle\lim_{x \rightarrow -1^{-}} \frac{x^2}{x^2-1}=\left[ \frac{1}{0^{+}} \right]=+\infty\\ \displaystyle\lim_{x \rightarrow -1^{+}} \frac{x^2}{x^2-1}=\left[ \frac{1}{0^{-}} \right]=-\infty\\ \end{array} \right.\\ \displaystyle\lim_{x \rightarrow +1} \frac{x^2}{x^2-1}= \left\{\begin{array}{l} \displaystyle\lim_{x \rightarrow +1^{-}} \frac{x^2}{x^2-1}=\left[ \frac{1}{0^{-}} \right]=-\infty\\ \displaystyle\lim_{x \rightarrow +1^{+}} \frac{x^2}{x^2-1}=\left[ \frac{1}{0^{+}} \right]=+\infty\\ \end{array} \right.\\ \end{array} \right.$$

Horizontales: $y=+1$

$$\left\{ \begin{array}{l} \displaystyle\lim_{x \rightarrow -\infty} \frac{x^2}{x^2-1}=1\\ \displaystyle\lim_{x \rightarrow +\infty} \frac{x^2}{x^2-1}=1\\ \end{array} \right.$$

Oblicuas: No tiene asíntotas oblicuas, ya que las tiene horizontales

Monotonía y extremos: $f(x)$ es derivable en $\mathbb{R} \setminus \left \{-1,+1 \right \}$

$$f(x)=\frac{x^2}{x^2-1} \Rightarrow f'(x)=\frac{-2x}{(x^2-1)^2}$$

Igualamos la derivada primera a cero y resolvemos la ecuación

$$f'(x)=\frac{-2x}{(x^2-1)^2}=0 \Leftrightarrow x=0$$ $$\left. \begin{array}{l} f'(x) > 0 \hbox{ en } (-\infty,-1) \cup (-1,0)\\ f'(x) =0 \hbox{ si } x=0 \\ f'(x) < 0 \hbox{ en } (0,+1) \cup (+1,+\infty)\\ \end{array} \right\} \Rightarrow \left. \begin{array}{l} f \nearrow \hbox{ en } (-\infty,-1) \cup (-1,0)\\ f \searrow \hbox{ en } (0,+1) \cup (+1,+\infty)\\ \end{array} \right\} \Rightarrow$$

$\Rightarrow f(x)$ tiene un máximo relativo en $x=0$

Curvatura y puntos de inflexión: $f'(x)$ es derivable en $\mathbb{R} \setminus \left \{-1,+1 \right \}$

$$f'(x)=\frac{-2x}{(x^2-1)^2} \Rightarrow f''(x)=\frac{2(3x^2+1)}{(x^2-1)^3}$$

Igualamos la derivada segunda a cero y resolvemos la ecuación

$$f''(x)=\frac{2(3x^2+1)}{(x^2-1)^3}=0 \Leftrightarrow x=\pm \sqrt{-\frac{1}{3}} \notin \mathbb{R}$$ $$\left. \begin{array}{l} f''(x) > 0 \hbox{ en } (-\infty,-1) \cup (+1,+\infty)\\ f''(x) < 0 \hbox{ en } (-1,+1)\\ \end{array} \right\} \Rightarrow \left. \begin{array}{l} f \hbox{ convexa en } (-\infty,-1) \cup (+1,\infty)\\ f \hbox{ cóncava en } (-1,+1)\\ \end{array} \right\} \Rightarrow$$

$\Rightarrow f(x)$ no tiene puntos de inflexión

Simetría: La función es simétrica par o respecto al eje Y

$$f(-x)=\frac{(-x)^2}{(-x)^2-1}=\frac{x^2}{x^2-1}=f(x)$$

Periodicidad: La función no es periódica

Tabla de valores:

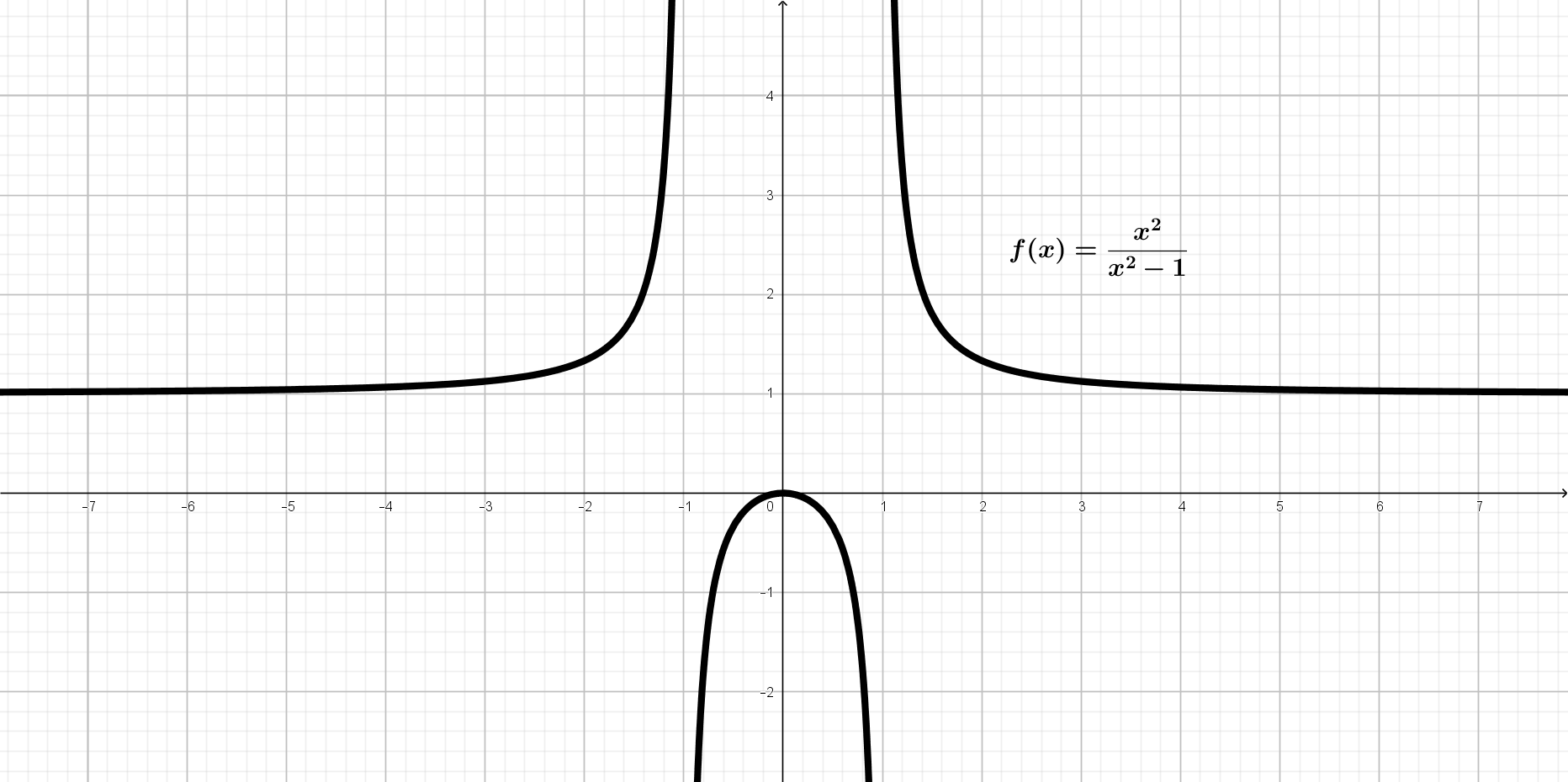
Problema (#3)

Representa gráficamente la función $\displaystyle{f(x)=x^4-2x^2+1}$

Solución:

Dominio:

$$Dom(f)=\mathbb{R}$$

Recorrido:

$$y=x^4-2x^2+1=(x^2-1)^2 \geq 0 \Rightarrow Rec(f)=[0,+\infty)$$

Puntos de corte con los ejes:

$\hbox{ Eje X } (y=0)$

$$x^4-2x^2+1=0 \Leftrightarrow (x^2-1)^2=0 \Leftrightarrow x^2-1=0 \Leftrightarrow x=\pm 1 \Rightarrow \left \{ \begin{matrix} P_1(-1,0)\\ P_2(+1,0)\\ \end{matrix} \right.$$

$\hbox{ Eje Y } (x=0)$

$$y=0^4-2 \cdot 0^2+1 \Leftrightarrow y=+1 \Rightarrow P_3(0,+1)$$

Continuidad: La función es continua en todo $\mathbb{R}$

Asíntotas:

Verticales: No tiene asíntotas verticales

Horizontales: No tiene asíntotas horizontales

$$\left\{ \begin{array}{l} \displaystyle\lim_{x \rightarrow -\infty} x^4-2x^2+1=+\infty\\ \displaystyle\lim_{x \rightarrow +\infty} x^4-2x^2+1=+\infty\\ \end{array} \right.$$

Oblicuas: No tiene asíntotas oblicuas

$$\left\{ \begin{array}{l} m = \displaystyle\lim_{x \rightarrow -\infty} \frac{x^4-2x^2+1}{x}=-\infty\\ m = \displaystyle\lim_{x \rightarrow +\infty} \frac{x^4-2x^2+1}{x}=+\infty\\ \end{array} \right.$$

Monotonía y extremos: $f(x)$ es derivable en todo $\mathbb{R}$

$$f(x)=x^4-2x^2+1 \Rightarrow f'(x)=4x^3-4x$$

Igualamos la derivada primera a cero y resolvemos la ecuación

$$f'(x)=4x^3-4x=0 \Leftrightarrow 4x(x^2-1)=0 \Leftrightarrow$$ $$\Leftrightarrow 4x(x-1)(x+1)=0 \Leftrightarrow \left\{ \begin{array}{c} x=0\\ \vee\\ x=-1\\ \vee\\ x=+1 \end{array} \right.$$ $$\left. \begin{array}{l} f'(x) > 0 \hbox{ en } (-1,0) \cup (+1,+\infty)\\ f'(x) =0 \hbox{ si } x=-1, x=0 \hbox{ o } x=+1\\ f'(x) < 0 \hbox{ en } (-\infty,-1) \cup (0,+1)\\ \end{array} \right\} \Rightarrow \left. \begin{array}{l} f \nearrow \hbox{ en } (-\infty,-1) \cup (-1,0)\\ f \searrow \hbox{ en } (0,+1) \cup (+1,+\infty)\\ \end{array} \right\} \Rightarrow$$ $$\Rightarrow \left\{ \begin{array}{l} f(x) \hbox{ tiene un mínimo relativo en } x=-1\\ f(x) \hbox{ tiene un máximo relativo en } x=0\\ f(x) \hbox{ tiene un mínimo relativo en } x=+1\\ \end{array} \right.$$

Curvatura y puntos de inflexión: $f'(x)$ es derivable en todo $\mathbb{R}$

$$f'(x)=4x^3-4x \Rightarrow f''(x)=12x^2-4$$

Igualamos la derivada segunda a cero y resolvemos la ecuación

$$f''(x)=12x^2-4=0 \Leftrightarrow x=\pm \frac{\sqrt{3}}{3}$$ $$\left. \begin{array}{l} f''(x) > 0 \hbox{ en } (-\infty,-\frac{\sqrt{3}}{3}) \cup (+\frac{\sqrt{3}}{3},+\infty)\\ f''(x) < 0 \hbox{ en } (-\frac{\sqrt{3}}{3},+\frac{\sqrt{3}}{3})\\ \end{array} \right\} \Rightarrow \left. \begin{array}{l} f \hbox{ convexa en } (-\infty,-\frac{\sqrt{3}}{3}) \cup (+\frac{\sqrt{3}}{3},+\infty)\\ f \hbox{ cóncava en } (-\frac{\sqrt{3}}{3},+\frac{\sqrt{3}}{3})\\ \end{array} \right\} \Rightarrow$$ $$\Rightarrow \left\{ \begin{array}{l} f(x) \hbox{ tiene un punto de inflexión en } x=-\frac{\sqrt{3}}{3}\\ f(x) \hbox{ tiene un punto de inflexión en } x=+\frac{\sqrt{3}}{3}\\ \end{array} \right.$$

Simetría: La función es simétrica par o respecto al eje Y

$$f(-x)=(-x)^4-2(-x)^2+1=x^4-2x^2+1=f(x)$$

Periodicidad: La función no es periódica

Tabla de valores:

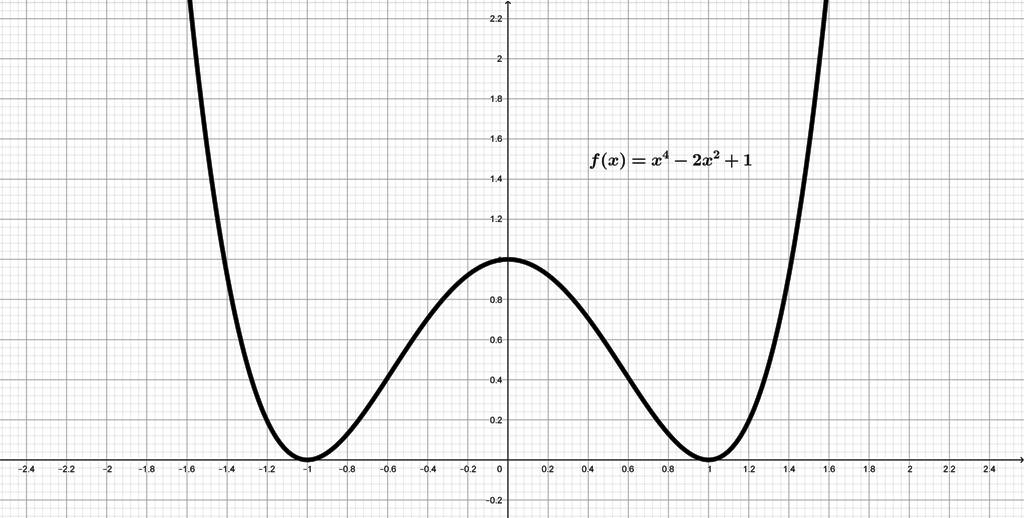
Problema (#4)

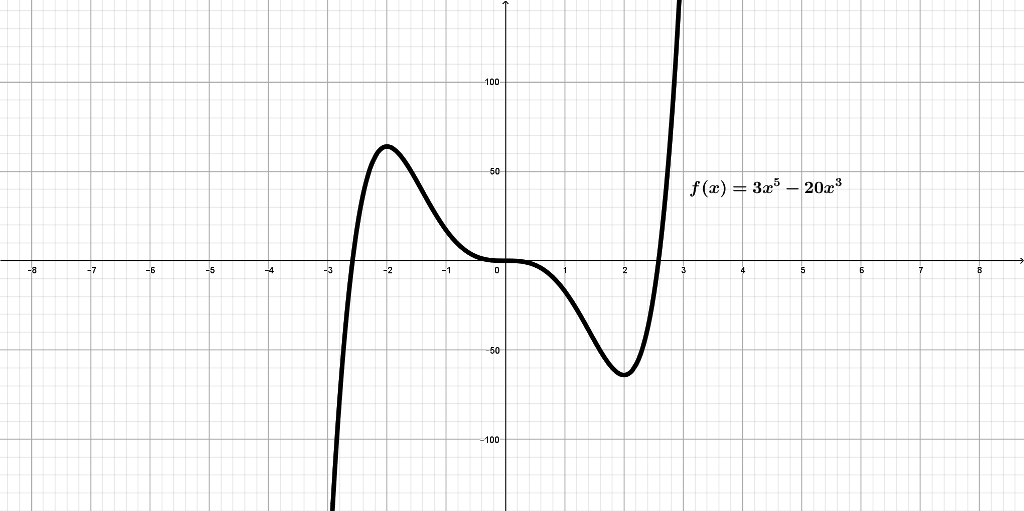
Representa gráficamente la función $\displaystyle{f(x)=3x^5-20x^3}$

Solución:

Dominio:

$$Dom(f)=\mathbb{R}$$

Recorrido:

$$Rec(f)=\mathbb{R}$$

Puntos de corte con los ejes:

$\hbox{ Eje X } (y=0)$

$$3x^5-20x^3=0 \Leftrightarrow x^3(x^2-20)=0 \Leftrightarrow$$ $$\Leftrightarrow x^3(x-2\sqrt{5})(x+2\sqrt{5})=0 \Leftrightarrow \left\{ \begin{array}{c} x=0\\ \vee\\ x=+2\sqrt{5}\\ \vee\\ x=-2\sqrt{5}\\ \end{array} \right. \Rightarrow \left \{ \begin{array}{c} P_1(0,0)\\ P_2(+2\sqrt{5},0)\\ P_3(-2\sqrt{5},0)\\ \end{array} \right.$$

$\hbox{ Eje Y } (x=0)$

$$y=3 \cdot 0^5-20 \cdot 0^3 \Leftrightarrow y=0 \Rightarrow P_1(0,0)$$

Continuidad: La función es continua en todo $\mathbb{R}$

Asíntotas:

Verticales: No tiene asíntotas verticales

Horizontales: No tiene asíntotas horizontales

$$\left\{ \begin{array}{l} \displaystyle\lim_{x \rightarrow -\infty} 3x^5-20x^3=-\infty\\ \displaystyle\lim_{x \rightarrow +\infty} 3x^5-20x^3=+\infty\\ \end{array} \right.$$

Oblicuas: No tiene asíntotas oblicuas

$$\left\{ \begin{array}{l} m = \displaystyle\lim_{x \rightarrow -\infty} \frac{3x^5-20x^3}{x}=+\infty\\ m = \displaystyle\lim_{x \rightarrow +\infty} \frac{3x^5-20x^3}{x}=+\infty\\ \end{array} \right.$$

Monotonía y extremos: $f(x)$ es derivable en todo $\mathbb{R}$

$$f(x)=3x^5-20x^3 \Rightarrow f'(x)=15x^4-60x^2$$

Igualamos la derivada primera a cero y resolvemos la ecuación

$$f'(x)=15x^4-60x^2=0 \Leftrightarrow 15x^2(x^2-4)=0 \Leftrightarrow$$ $$\Leftrightarrow 15x^2(x-2)(x+2)=0 \Leftrightarrow \left\{ \begin{array}{c} x=0\\ \vee\\ x=+2\\ \vee\\ x=-2\\ \end{array} \right.$$ $$\left. \begin{array}{l} f'(x) > 0 \hbox{ en } (-\infty,-2) \cup (+2,+\infty)\\ f'(x) =0 \hbox{ si } x=-2, x=0 \hbox{ o } x=+2\\ f'(x) < 0 \hbox{ en } (-2,+2)\\ \end{array} \right\} \Rightarrow \left. \begin{array}{l} f \nearrow \hbox{ en } (-\infty,-2) \cup (+2,+\infty)\\ f \searrow \hbox{ en } (-2,+2)\\ \end{array} \right\} \Rightarrow$$ $$\Rightarrow \left\{ \begin{array}{l} f(x) \hbox{ tiene un máximo relativo en } x=-2\\ f(x) \hbox{ tiene un mínimo relativo en } x=+2\\ \end{array} \right.$$

Curvatura y puntos de inflexión: $f'(x)$ es derivable en todo $\mathbb{R}$

$$f'(x)=15x^4-60x^2 \Rightarrow f''(x)=60x^3-120x$$

Igualamos la derivada segunda a cero y resolvemos la ecuación

$$f''(x)=60x^3-120x=0 \Leftrightarrow 60x(x^2-2)=0 \Leftrightarrow$$ $$\Leftrightarrow 60x(x-\sqrt{2})(x+\sqrt{2})=0 \Leftrightarrow \left\{ \begin{array}{c} x=0\\ \vee\\ x=+\sqrt{2}\\ \vee\\ x=-\sqrt{2}\\ \end{array} \right.$$ $$\left. \begin{array}{l} f''(x) > 0 \hbox{ en } (-\infty,-\sqrt{2}) \cup (0,+\sqrt{2})\\ f''(x) < 0 \hbox{ en } (-\sqrt{2},0) \cup (+\sqrt{2},+\infty)\\ \end{array} \right\} \Rightarrow \left. \begin{array}{l} f \hbox{ convexa en } (-\infty,-\sqrt{2}) \cup (0,+\sqrt{2})\\ f \hbox{ cóncava en } (-\sqrt{2},0) \cup (+\sqrt{2},+\infty)\\ \end{array} \right\} \Rightarrow$$ $$\Rightarrow \left\{ \begin{array}{l} f(x) \hbox{ tiene un punto de inflexión en } x=-\sqrt{2}\\ f(x) \hbox{ tiene un punto de inflexión en } x=0\\ f(x) \hbox{ tiene un punto de inflexión en } x=+\sqrt{2}\\ \end{array} \right.$$

Simetría: La función es simétrica impar o respecto al origen de coordenadas

$$f(-x)=3(-x)^5-20(-x)^3=-3x^5+20x^3=-(3x^5-20x^3)=-f(x)$$

Periodicidad: La función no es periódica

Tabla de valores: