Matemáticos de ayer y de hoy: Leonhard Euler (1707-1783)
Leonhard Paul Euler (1707-1783), fue un matemático y físico suizo, considerado uno de los más grandes y prolíficos de todos los tiempos. Nació el 15 de abril de 1707 en Basilea, Suiza, y falleció el 18 de septiembre de 1783 en San Petersburgo, Imperio ruso.
Desde temprana edad demostró habilidades para las matemáticas, lo que le ganó la estima del patriarca de los Bernoulli, Johann Bernoulli, uno de los más eminentes matemáticos de su tiempo y profesor suyo en la Universidad de Basilea. Cuando tenía trece años se matriculó en la Universidad de Basilea. En 1723 se graduó en dicha institución y cuatro años más tarde fue invitado personalmente por Catalina I para convertirse en asociado de la Academia de Ciencias de San Petersburgo. Cuando tenía diecinueve años finalizó su doctorado con una tesis acerca de la propagación del sonido.
Euler es muy conocido por el número de Euler (e), número que aparece en muchas fórmulas de cálculo y física. Realizó importantes descubrimientos en áreas tan diversas como el Cálculo o la Teoría de Grafos. A causa de su extrema dedicación al trabajo, perdió la visión del ojo derecho, hecho que no afectó ni a la calidad ni al número de sus hallazgos. Dos de sus obras más importantes fueron “La Introductio in analysin infinitorum” (1748) y “La institutione calculi differentialis” (1755).
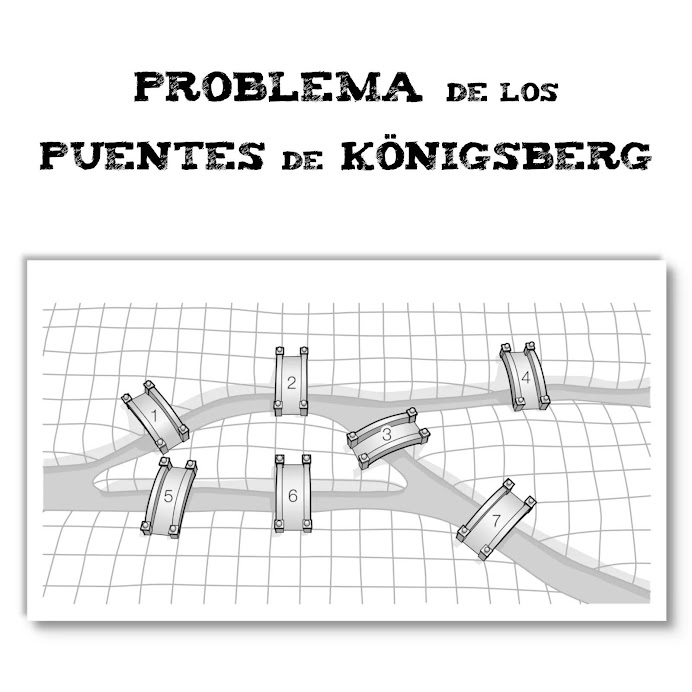
En 1736, resolvió el famoso problema matemático de "Los puentes de Königsberg". La ciudad de Königsberg, que ahora es la ciudad rusa de Kaliningrado, estaba atravesada por el río Pregolia. El río se bifurcaba y rodeaba la isla Kneiphof, dividiendo el terreno en cuatro regiones distintas. Estas regiones estaban unidas por siete puentes. El problema, formulado en el siglo XVIII, consistía en encontrar un recorrido para cruzar a pie toda la ciudad pasando solo una vez por cada uno de los puentes y regresando al mismo punto de inicio.
Demostró que no es posible encontrar tal recorrido. Su solución no se basó en probar todos los recorridos posibles (un método de fuerza bruta), sino que proporcionó una solución generalizada que puede aplicarse a cualquier territorio con ciertas restricciones de acceso. Esta solución y el análisis del problema dieron lugar a la Teoría de Grafos.
En 1741, por invitación de Federico II el Grande, se trasladó a la Academia de Berlín, donde refinó los métodos y las formas del Cálculo Integral. A raíz de ciertas tensiones con Federico el Grande, regresó nuevamente a Rusia en 1766, donde al poco de llegar perdió la visión del otro ojo.
Construyó un cuadrado mágico 8x8, conocido como el Cuadrado Mágico de Euler. En este cuadrado, cada fila y cada columna suman 260. Sin embargo, las diagonales no suman 260, por lo que no llega a ser un cuadrado mágico en el sentido estricto. Sin embargo, al detenerse en la mitad de cada fila o columna, la suma es 130, exactamente la mitad de 260.
Además, este cuadrado tiene una propiedad muy interesante: Si te imaginas el cuadrado en un tablero de ajedrez (8x8), puedes ir desde el número 1 hasta el 64, de forma consecutiva, siguiendo el movimiento del caballo, sin pasar dos veces por la misma casilla del tablero.